Impact angle of impactors decaying from circular orbits in an ancient Mars atmosphere

1. Introduction

Moonlets from an equatorial debris disk caused by a giant impact (a mechanism by which Phobos and Deimos may have formed (Craddock 2011; Rosenblatt 2011), may have had slowly decaying orbits leading to craters formed at low impact angles (< 5°). The absence of crater morphologies consistent with very low impact angles has been used to argue against the spiralling moonlet hypothesis for the formation of elongated craters (Bottke et al. 2000). The absence of comprehensive atmospheric entry and impact modelling for decaying moonlets leaves open the possibility that some only moderately elongated craters on Mars were formed by decaying moonlets in a thicker atmosphere. Indeed, the 12.5km spatial separation and apparent 3-3.7Ga age and cogenesis of double-oblique impact craters observed by (Chappelow and Herrick 2008) could be inconsistent with formation by a fast (i.e. non-moonlet) meteorite impactor unless a thicker atmosphere provided drag to increase impact angle during spiralling.

2. Method

To explore the effect of ancient atmospheric conditions on the impact angle of potential spiralling moonlets, we construct a simple 2D model to spiral down a moonlet from the top of a hypothetical Mars atmosphere. A body that is at mean circular orbital velocity at the top of the atmosphere,

experiences gravitational pull

and atmospheric drag,

Where G is the gravitational constant, M_m is the mass of Mars, r is the distance between the centres of mass of the impactor and Mars’, C_D is the coefficient of drag, 𝜌 is the atmospheric density, and A is the cross-sectional area of the impactor (with respect to the velocity direction).

The model proceeds at each time step (1s) by updating the impactor velocity with a vector of the resultant acceleration, calculated using instantaneous gravitational and atmospheric drag forces. We simulate impact angle, retrieved at the point of contact between spherical impactors and the Mars surface for plausible parameter ranges for impactors and ancient Mars atmosphere.

C_D is typically determined experimentally, and is a function of many parameters. At low speeds and for a small spherical projectiles, C_D  ~ 0.5 (Miller and Bailey 1979). For large projectiles and mach numbers > 1, behaviour of C_D becomes complex and may reach values > 1. To account for this we run simulations for a range of C_D up to 1.1.

Impactors 10m to 10km in diameter, surface atmospheric pressures 5 to 500 mbar, coefficients of drag 0.5 to 1.1, and densities covering the range between Phobos and Deimos (1400-1900 kg m^-3). An atmospheric temperature profile from  (Schofield et al. 1997) was used, and linearly interpolated as a function of altitude.

We assumed a present day atmospheric composition, with component fractions of 0.7532, 0.227, 0.016 and 0.08 of CO₂, N₂, Ar and CO, respectively. It is highly likely that an ancient Mars atmosphere had a different composition. As a cursory assessment of the potential impact of different atmospheric composition, we note that substituting 20% of Mars CO₂ fraction for N₂, the mean molecular mass, 𝜇, would change from 0.0455 to 0.0415, a shift of ~9%. Given that 𝜇 appears only a first order denominator in the calculation of scale height (H = RT/𝜇g) we do not expect uncertainty on past atmospheric composition to have a major impact on our conclusions.

A summary of the parameters used is shown in Table 1. We ran the model for all permutations of the parameter grid, yielding ~2.6x10⁵, model runs.

Table 1: Domain and sampling intervals for parameter space explored for spiralling impactors.

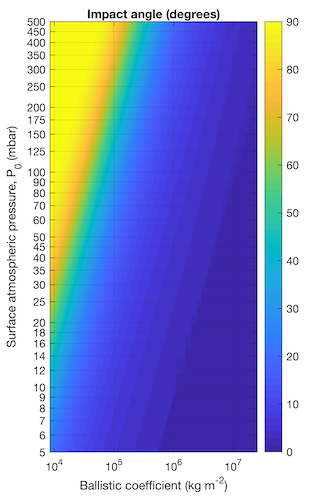
Figure 1: Impact angle as a function of surface atmospheric pressure (mbar) and ballistic coefficient (BC). Surface is a bilinear interpolation of BC run over the parameters listed in Table 1.

3. Discussion

With a drag coefficient of 0.5, Phobos has a ballistic coefficient ~ 8x10⁷ kg m^-2, while Deimos’ is ~2.4 x 10⁶ kg m^-2. Both moons are therefore sufficiently large and dense that their impact angle would not be substantially modified by atmospheric drag, even for a 0.5 bar atmosphere. However, moonlets decaying from a quasi-stable equatorial debris disk has been proposed to be in the range 1-4km (Rosenblatt et al. 2016). A 1km diameter object with Deimos density would have a BC ~1.8x10⁶. Such an object would experience a shift in impact angle of several 10s of degrees in atmospheres > 100 mbar.

Importantly, we note that the model does not account for non-spherical shapes, heterogeneous density distribution in the impactor, or fragmentation of impactors. Fragmentation would produce a group of impactors, each with lower ballistic coefficients than the parent impactor, and therefore whose impact angle may be steeper than if fragmentation did not occur.

4. Conclusions

We find that apparent lack of very oblique impacts that should be expected from decaying moonlet hypothesis could be due to increased atmospheric drag in an ancient, thicker atmosphere. Based on a simplistic model, impact angle deviations > 10° (compared to present day) are possible in atmospheres of few 100 mbars, for objects with low ballistic coefficients in the ~sub-km diameter range.

5. References

Bottke, W. F., Love, S. G., Tytell, D., and  Glotch, T. 2000. “Interpreting the Elliptical Crater Populations on Mars, Venus, and the Moon.” Icarus 145(1): 108–21.

Chappelow, J. E., and R. R. Herrick. 2008. “On the Origin of a Double, Oblique Impact on Mars.” Icarus 197(2): 452–57.

Craddock, R. A. 2011. “Are Phobos and Deimos the Result of a Giant Impact?” Icarus 211(2): 1150–61.

Miller, D. G., and Bailey, A. B. 1979. “Sphere Drag at Mach Numbers from 0·3 to 2·0 at Reynolds Numbers Approaching 107.” Journal of Fluid Mechanics 93(3): 449–64.

Rosenblatt, P. 2011. “The Origin of the Martian Moons Revisited.” Astronomy and Astrophysics Review 19(1).

Rosenblatt, P. et al., 2016. “Accretion of Phobos and Deimos in an Extended Debris Disc Stirred by Transient Moons.” Nature Geoscience 9(8): 581–83.

Schofield, J. T. et al. 1997. “The Mars Pathfinder Atmospheric Structure Investigation/Meteorology (ASI/MET) Experiment.” Science 278(5344): 1752–58.