A 3D, time-dependent, non-LTE radiative transfer code for radio and far-infrared observations of cometary comae and planetary exospheres

Abstract 

We present results from a new 3D numerical code for solving the time-dependent equations of statistical equilibrium in cometary comae and planetary exospheres. This enables a more accurate calculation of the molecular excitation, for simulations of far-infrared and submillimeter emission lines. Our non-LTE radiative transfer code is based on the LIME (Line Modelling Engine) source code. It includes a robust 3D calculation of the internal radiation field and represents an improvement over the previous (steady-state) model for the case of rapidly expanding cometary atmospheres and planetary exospheres. Here we compare the results of the level population distributions for HCN and CO in a cometary coma using both time-dependent and steady-state solutions, and consider possible future applications to plumes from icy moons.

1. Introduction

The ability to accurately model astronomical observations in low-density environments, where local thermodynamic equilibrium cannot be assumed, is dependent on an accurate solution of the radiation transfer problem. Examples include the study of cometary volatiles, icy moon atmospheres, outflows, and young stellar objects. Furthermore, spacecraft missions and ground-based telescope facilities such as the Atacama Large Millimeter-submillimeter Array (ALMA) allow for very high-resolution astronomical observations, which require detailed models capable of handling the interaction between multiple molecular species in arbitrary geometries.

LIME (Line Modeling Engine) is a non-LTE, 3D radiative transfer code for submillimeter to far-infrared emission, introduced in 2010 [1]. In addition to transitions due to collisional excitation and spontaneous radiative decay, LIME also simulates transitions due to radiative excitation and radiation trapping via a 3D Monte Carlo treatment of the radiation field. However, the efficacy of LIME, and similar methods, for dynamic environments including expanding (cometary) atmospheres is limited, since the equations of statistical equilibrium are solved as a function of spatial coordinates using the assumption of steady-state. We have built upon the LIME codebase to create a new module that dispenses with the assumption of steady-state by implementing a time-dependent solution for the gas trajectories, following the formalism in reference [2]. In addition to being capable of performing the full 3D treatment of the radiation field, it also provides the option of using the escape probability (Sobolev’s) method [2]. While less accurate than the Monte Carlo photon trapping method, the escape probability method provides a less computationally demanding alternative, ideal for fast calculations or situations where radiation trapping does not play a significant role. Our new model also includes electron collisional transitions, which can be particularly important in cometary comae.

2. Equations of statistical equilibrium

The time-dependent evolution of the level populations is given by the coupled differential equations

 

where p_ij is the transition rate from level i to j, and n_i is the fractional population of level i. In the case of steady-state, the left-side of the equation is set equal to zero. The transition rates are given by                                                                 

where C_ij denotes the collisional transitions from level i to j, B_ij is the induced emission or absorption rate, A_ij is the spontaneous emission rate, and J_ij is the radiation mean intensity averaged over 4π and integrated over the line. When the escape probability (Sobolev’s) approximation is used, equation (2) is simplified to

where β_ij is the photon escape probability. For a more detailed description of the transition rate terms, see references [2, 3].

3. Method

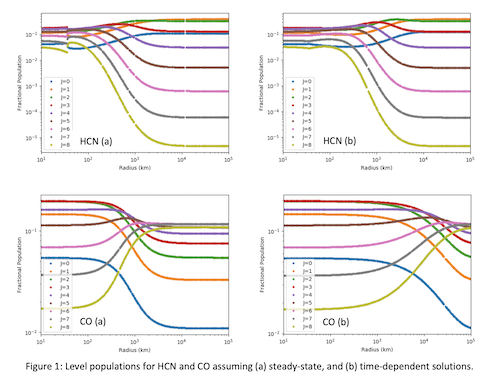
We consider two models for a uniformly-expanding H₂O-dominated cometary coma: one with an HCN abundance of 0.1% (photodissociation rate β_HCN = 1.5 × 10^-5), and another with a CO abundance of 5% (β_CO = 7.5× 10^-7). Table 1 contains the parameters that are common to both models. The collisional transition rates with water were retrieved from the LAMDA database [4], assuming C_ij (H₂O) = C_ij (H₂). Electron collisional rates were calculated following the formalism in reference [3]. The coma outflow is followed from the nucleus (r = 2.5 km) out to 10⁵ km. The fractional energy level populations (as a function of rotational quantum number J) were calculated using (a) the steady-state and (b) the time-dependent methods. Results for J = 0 to 8 are shown in Figure 1.

4. Results

5. Summary

The level populations undergo a characteristic evolution from LTE in the collisional-dominated regime close to the nucleus, towards fluorescence equilibrium in the outer coma. The dynamical effects included in the time-dependent treatment (panels b) are evident through the delayed onset of the departure from LTE as a function of radius, which occurs due to the dynamical (outflow) timescale being less than the excitation timescale. Consequently, the time-dependent model provides more accurate results than the steady-state model, particularly in the case of low H₂O production rates, where departure from LTE occurs too close to the nucleus if steady-state is assumed. The effect is more pronounced for CO due to its longer radiative lifetime. This effect should therefore be taken into account in future models for expanding cometary comae and icy moon exospheres.

6. References

[1] C. Brinch and M. R. Hogerheijde. A&A, 523, A25, 2010.

[2] D. Bockelee-Morvan. A&A, 181, 169, 1987.

[3] V. Zakharov et al. A&A, 473, 303, 2007.

[4] Schöier, F.L., van der Tak, F.F.S., van Dishoeck E.F., Black, J.H., A&A, 432, 369, 2005.