Modelling the atmosphere of lava planet K2-141b: implications for photometry and spectroscopy

Introduction 

Lava planets orbit close enough to their star that parts of their surface are molten. Temperatures on the dayside are often hot enough to vaporise rocks, which create a thin mineral vapour atmosphere. Lava planets are currently one of the best targets to observe rocky worlds outside the solar system.

We simulate the steady-state vapour-pressure driven flow of the recently discovered exoplanet K2-141b via a 1D hydrodynamical model. This model produces the atmospheric pressure, temperature, and wind velocity as well as evaporation and condensation rates. We then infer the magma ocean circulation required for mass balance and simulate how our results would affect photometric and spectroscopic observation.

Methods 

The hydrodynamical model that we used was first developed by Ingersoll et al. (1985) to model the thin atmosphere of Io. The model was subsequently adapted by Castan and Menou (2011) to model lava planets such as Kepler 10-b and 55 Cnc-e. Although greatly idealized, these calculations are robust to the supersonic winds and atmospheric collapse that result from the extreme day-to-night temperature contrast.

Before introducing the system of equations that makes up the 1D model, it is important to list the assumptions and limitations of our idealized case. First, we assume a hydrostatically bound atmosphere that is thin enough to not absorb any radiation. Second, we assume a turbulent and well-mixed atmosphere, which leads to a vertically constant wind profile. Third, we assume only a single constituent which allows us to ignore chemical processes that greatly complicates our problem. Another idealization is the neglect of the planet’s rotation, which allows for symmetry about the subsolar/antisolar axis making the problem 1D.

The system of equations below describes the conservation of mass (1), momentum (2), and energy (3) which are solved for state variable pressure, P, temperature, T, and wind velocity, V; P and T are evaluated at the top of the turbulent boundary layer. The angular distance from the subsolar point, θ is the only independent variable.

In equation (1)-(3), the important flux variables are E, the surface mass flux, τ , the surface drag, and Q, the surface energy flux. Detailed derivation along with calculations of the surface fluxes can be found in Ingersoll et al. (1985).

Results 

We simulate the atmosphere of K2-141b for atmospheric constituent SiO₂ (due to abundance) or Na (due to volatility). The solution strongly depends on the saturated vapour pressure relation with temperature which is provided by Schaefer and Fegley (2009). Figures (1) and (2) below show the state variables solution for SiO₂ and Na atmospheres, respectively.

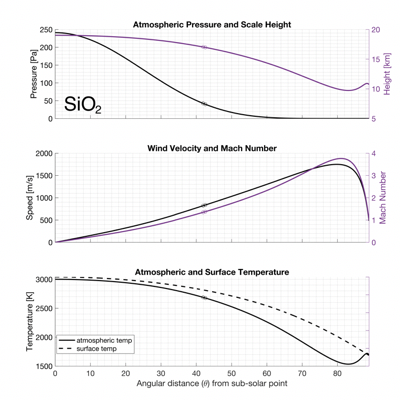
Figure 1: solution to SiO₂ atmosphere. Top panel: atmospheric boundary-layer pressure (left) and scale height (right). Middle panel: wind velocity (left) and Mach number (right). Bottom panel: atmospheric and surface temperature.

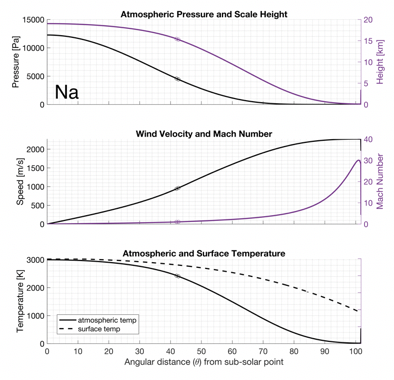
Figure 2: solution to Na atmosphere. The format is exactly the same as Fig. (1).

Since Na is much more volatile than SiO₂, the Na atmosphere is much thicker, as expected. The Na atmosphere also extends further than SiO₂ atmosphere. However, the SiO₂ atmosphere retains heat better which makes it much warmer than its Na counterpart.

If we presume a pure SiO₂ atmosphere, then we can infer the magma ocean circulation that balances out the mass transport by the atmosphere. The inferred ocean circulation depends on the ocean depth and the horizontal mass transport. The magma ocean depth can be approximated by first assuming a vertically constant temperature profile for the surface and determine the pressure at which liquid SiO₂ change phase. The horizontal mass flux transported by the atmosphere can be approximated by integrating the precipitation rate. The figure below shows the magma ocean properties for the SiO₂ case.

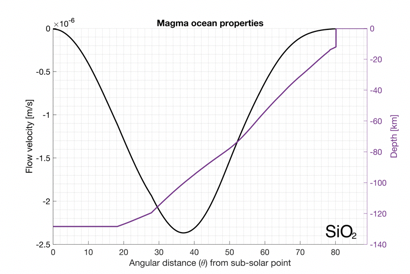
Figure 3. Left: velocity of magma ocean return flow. Negative values denote mass flow towards the subsolar point. Right: ocean depth.

We do the same analysis for the Na case where the ocean is set to have the same Na to SiO₂ ratio as the Bulk Silicate Earth composition. This yields an ocean velocity that is 10⁴ times the speed of the SiO₂ case. This suggests that maintaining mass balance for SiO₂ is much easier than for Na.

We do the same analysis for the Na case where the ocean is set to have the same Na to SiO₂ ratio as the Bulk Silicate Earth composition. This yields an ocean velocity that is 10⁴ times the speed of the SiO₂ case. This suggests that the slow return flow may prohibit a steady-state Na atmosphere.

To simulate observations of K2-141b’s atmosphere, we calculate the radiative flux emitted at a given wavelength corresponding to spectral features of SiO₂ and Na. We then integrate the flux of the visible hemisphere of K2-141b to obtain its orbital phase curve.

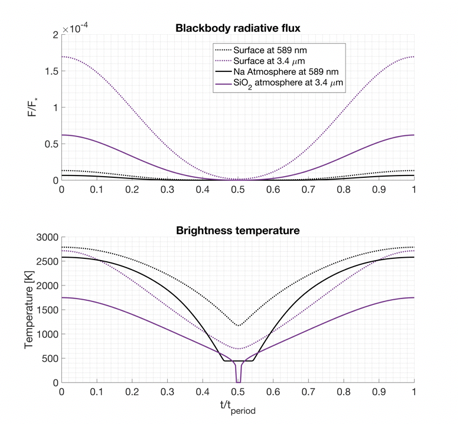
Figure 4. Top panel: predicted phase curve of K2-141b for a Na atmosphere (black lines) or for a SiO₂ atmosphere (purple lines). The chosen wavelengths are near spectral features of SiO₂ at 3.4 m and of Na at 589 nm. Bottom: Disk-integrated planetary brightness temperature for the two scenarios.

Discussion

Idealized 1D models provide important insights for future observations of K2-141b and likewise of many other lava planets. Our results show that the atmosphere will fully condense before reaching the nightside for both cases. We also show that a steady-state Na atmosphere is difficult to achieve given the slow return flow through a SiO₂ ocean. Finally, the thinner and hotter SiO₂ atmosphere may be easier to observe due to its greater terminator at the limb of the planet as seen during transit.

Acknowledgement 

We would like to thank R. Pierrehumbert for his guidance. This work was made possible by the Natural Science and Engineering Research Council (NSERC) of Canada’s Collaborative Research and Training Experience (CREATE) Program for Technology for Exo-planetary Sciences (TEPS).

References 

Castan and Menou, 2011, APJ, 743, L36

Ingersoll, Summers, and Schlipf, 1985, Icarus, 64, 375

Schaefer and Fegley, 2009, APJ, 703, L113