Latest update of Mercury geodetic parameters with altimetric crossovers from the Mercury Laser Altimeter (MLA)

Based on previous applications of laser altimetry to planetary geodesy at GSFC [Mazarico et al. (2014)], we use the recently developed PyXover software package to analyze altimetric crossovers from the Mercury Laser Altimeter (MLA) and improve geodetic parameters via least squares (LS) minimization of crossover discrepancies.
We simultaneously solve for orbital corrections for each MESSENGER track, for the geodetic parameters of the IAU recommended orientation model for Mercury [Archinal et al, 2018], and for the Mercury Love number h₂.
We calibrate the formal errors of our solution based on closed-loop simulations and on the level of independence from \emph{a priori values and data selection.

Data description:

From  March  2011  to  April  2015, the MESSENGER spacecraft orbited Mercury in a highly elliptical, near-polar orbit with a periapsis of ~200-400 km, an apoapsis between ~1.5-2 x 10^4 km, and an orbital period of 12 hrs initially and reduced  to  8  hrs  after  one  year. The spacecraft was  within  ranging  distance for the onboard MLA over  15-45 min periods near periapsis, typically at latitudes > 30 deg N.

MLA collected over 22 million measurements of surface height with a vertical precision of ~1 m and an accuracy of ~10 m. The total MLA dataset contains ~3,200 tracks and ~3 million crossovers, i.e., instances where  two  ground-tracks  intersect.  Because  of  the  elliptical  orbit,  the  laser spot  size  on  the  surface  varied  between ~10 - 100 m, while  the average distance  between each  crossover and its bracketing observations was ~200 m.

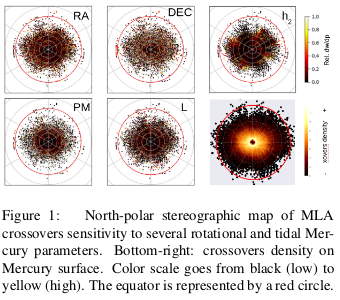
These  crossovers provide an opportunity to measure Mercury’s  orientation  and  rotation (see Fig.1).
Independent  confirmation  and  refinement  of  the IAU  libration  model,  developed  from  ground-based radar measurements [Margot et al. 2009], is important as it has implications  for  the  moment  of  inertia  of  the  outer  solid  shell and  thus  the  mass  distribution,  internal  structure,  and thermal  evolution  of  Mercury [Phillips et al. (2018), Genova et al. (2019)].

Processing and solution strategy:

Each  crossover  is  the  intersection  of  two  separate 
ground-tracks. It can be thought of as a differential measurement between two  distinct  observations of the same surface location at two different 
times. Any  difference  in  height  at the crossover  point  is  mainly due to the following  effects: 
(1)  Errors  in  the spacecraft  orbit and  attitude, or MLA  boresight  orientation,  (2)  interpolation  errors  of the surface topography between MLA footprints, and (3) geophysical signal due, e.g., to mismodeled  time-varying  planetary  rotation or to tidal vertical motions.

We perform the analysis of MLA data with the PyXover python code, whose modular structure is sketched in Fig.2.
Laser altimetry ranges are geolocated to the planetary surface and partial derivatives of the ground-tracks are computed with respect to the chosen parameters by finite differencing. Initial geolocation is based on the MESSENGER orbit navigation reconstruction by KinetX and on the values provided by the IAU for Mercury orientation [Archinal et al, 2018]. Values for the Love numbers h₂ and l₂ are set to 0 in our a priori tidal model.
Horizontal coordinates of crossover points are recovered in local stereographic projection in a two-step process, to balance computational time.
Expected elevations at intersection points are then interpolated from neighbouring points on each track. Their discrepancies w constitute the observation residuals to be minimized in the LS procedure.
Huber weighting is then applied to the crossovers depending on the reliability of the orbital tracks involved, on the off-nadir angle of the spacecraft and on inter-point distances. Crossovers with abnormally large discrepancies are strongly down-weighted in our analysis. 
We minimize the total RMSE of crossover discrepancies within a penalised LS with weights determined by Variance Component Estimation (VCE). 
The resulting corrections to MESSENGER orbits and Mercury geodetic parameters are then applied to update the a priori for the subsequent iteration, until convergence is reached.

Parametrization and error assessment:
Formal errors provided by LS and VCE are notoriously under-estimated. We thus perform additional analysis to consider systematic error sources, such as the chosen apriori values and data selection. In particular, we measure the stability of the solutions resulting from different Doppler reconstructions of MESSENGER orbits (KinetX and [Genova et al, 2018]) and from both IAU [Archinal et al, 2018] and [Genova et al, 2019] values for Mercury rotational parameters. Also, we process multiple sub-samples of 500,000 crossovers (max 20% in common, stratified by latitude to conserve the overall geographical distribution) and we verify the dispersion of the solutions at convergence.
Moreover, we conduct extensive simulations with time-of-flight ranges consistently generated from realistic topography to analyze the impact of the interpolation error and the reliability of the recovery in different scenarios and parametrizations. 

Processing of MLA crossovers:

Finally, we perform a weighted LS solution of orbit corrections and geodetic parameters based on the presented processing setup.
We base our solution on a set of 10⁶ crossovers selected according to their computed weight (i.e., their quality) and to ensure a balanced geographical distribution. 
We iterate the solution until convergence is reached, i.e., parameters changes are well below formal errors (<10 iterations). Observation weights are re-evaluated at each iteration down to the convergence of discrepancies RMSE at 5% and then fixed.

We check the reduction of the RMSE of post-fit discrepancies w, as shown in Fig.3, the evolution of VCE derived weights and the consistency of topography maps to evaluate the improvements.

Our results for some geodetic parameters are shown in Fig.4 and are consistent with previous solutions provided by other groups using various techniques (camera and altimetry, Doppler, Earth-based radar). 

Error bars are calibrated based on both closed-loop simulations and the analysis of systematic errors outlined in the previous section.
We will discuss the recovered h₂ and our determination of Mercury rotational parameters at the meeting.

Acknowledgements
S. Bertone acknowledges support by the Swiss National Science Foundation within the Advanced Postdoc Mobility program and by NASA’s Planetary Science Division Research Program through the CRESST II cooperative agreement. The MLA data were processed on the GSFC NCCS ADAPT cluster.