A possibility to exist the trapped energetic particles zone near Mercury

We consider the possibility of radiation belts existence near Mercury. The study is carried out both using the Størmer theory for charged particles motion, in which zones of allowed and forbidden motion in an axially symmetric magnetic field are considered, and trajectories analysis.

The internal magnetic field of Mercury was discovered in 1974 by the Mariner 10 spacecraft. In [1] values for the dipole field at the Mercury equator B_eq=192 nT and the north offset of the dipole dz=0.18 R_M (where R_M=2439 km is Mercury radius) were obtained, which were subsequently confirmed during the MESSENGER spacecraft flybys in 2011–2015. In our work, we also introduced a formal magnetopause at the distance R_mp=1.4 R_M.

Allowed zones of particle motion are described in the Størmer theory in cylindrical coordinates by the inequality:

Q = 1 – (P_φ/(pρ) – qA_φ/(pc))² ≥0,

where P_φ is particle generalized angular momentum, p is its momentum, q is its charge, c is the speed of light, and A_φ is magnetic field vector potential (for more details see [2]). Equality Q=0 defines the boundaries of allowed zones, and Q=1 is a force line equation. We consider such A_φ, which is the sum of the potentials of pure dipole field and uniform external field b_e directing along the z-axis and approximating magnetopause currents fields.

Further, we measure lengths in units of the Størmer radius r_st=√(qM/(pc)), where M is the absolute value of dipole magnetic moment. This radius acts as a scale factor. In a pure dipole field, it determines the curvature radius of the unstable circular trajectory lying in the dipole equatorial plane. The second Størmer integral of motion, arising as a result of axial symmetry, is the dimensionless parameter γ=P_φ/(2pr_st), which defines the shape and size (in r_st) of allowed and forbidden zones. After their substitution, the inequality for Q takes the form:

Q = 1 – (2γ/ρ – ρ/r³ – Gρ)² ≥0,

where we introduce a coefficient G=b_er_st³/(2B_eqR_M³). In a pure dipole field for γ>1, there are two allowed zones: the infinite external and internal that is isolated and enclosed in the inner part of the sphere with radius r_st. For external homogeneous field, in our calculations we used the value b_e=50 nT, whence G=–4.2717. In this case, when γ>–1/(8G) there is also a closed in space internal allowed zone.

Let us consider the motion of nonrelativistic particles, specifically protons, which trajectories start in points located at the dipole equatorial plane. Then an analysis based on Størmer’s theory can be connected with the classical description of particle motion through the initial pitch angle α_eq and phase angle χ_eq as follows:

γ = 0.5 (1/R + R sin α_eq sin χ_eq + R²G),

where R is the initial distance from the dipole.

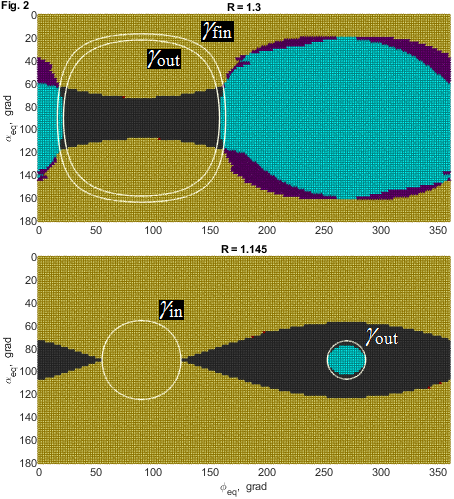
On one hand, the condition of an internal allowed zone appearance from under the planet’s surface (that is possible, if r_st is greater then planet radius), which occurs when γ=γ_in, must be fulfilled. On the other hand, the trajectories should not go beyond the magnetopause. The internal allowed zone firstly touches the magnetopause at γ=γ_out, and the final disappearance of the captured trajectories occurs at γ_fin<γ_out. As a consequence, in the case of Mercury only capturing of particles with kinetic energy K less than a few hundred keV can be possible. Particles within the internal allowed zone oscillate between mirror points, the positions of which depend on their initial pitch angles. Capturing of a particle possible if its mirror points is located above the planet’s surface, and the imprecision of the conservation of the 1^st adiabatic invariant sin²α/B=const [3] does not lead to their significant displacement within the time T of interest to us. The description of the capture region located in the vicinity of the plane of the magnetic equator can be pictorially expressed by the formula:

where each elementary trajectory ‘traj.’ lies inside the allowed zone, α₀ is α_eq for the start position on the base of field line Q=1, α_th1 and α_th2 are the threshold values of α₀ (Fig. 1), that as well as γ_fin slightly depend from T. Taking into account the variability of the Mercury magnetosphere, we chose prolonged T=20 minutes.

We considered sets of trajectories of 3∗10⁴ protons with K=100 keV, the starting point of which was located at different distances R. Their motion was examined over a time interval of 60 seconds, in two directions in time. A particle that was thus captured for more than 2 minutes, which is approximately three times larger then their period of drift motion, was considered as captured (see Table).

R (RM)	percentage of captured particles
1.10	19.6
1.15	25.2
1.20	19.0
1.25	16.7
1.30	13.8
1.35	9.6

 

To describe the situation at the different points R, we also calculated maps showing the dependence of particles history on their initial pitch and phase angles (Fig. 2). Yellow color denotes particles colliding with the planet’s surface both in the past and in the future; red—either in the past or in the future; dark gray—capturing in the period under review; purple—arriving from outside the magnetopause and colliding with the surface, or vice versa; blue—flying by. We also drew the isolines γ_in, γ_out and γ_fin on these maps. As it can be seen, the flow of particles at a given point in the magnetosphere of Mercury does not consist solely of trapped, precipitated, or transit particles. At the same point, both passing particles and particles making less than one drift revolution before a collision with the planet surface can be detected.

[1] Alexeev I.I., Belenkaya E.S., Bobrovnikov S.Yu. et al. // J. Geophys. Res. Space Physics. 2008. V. 113. A12210.

[2] Lavrukhin A.S., Alexeev I.I., Tyutin I.V. // Ann. Geophys. 2019. V. 37. P. 535–547.

[3] Kuznetsov S.N., Yushkov B.Yu. // Plasma Physics Reports. 2002. V. 28, No. 4, pp. 342–350.