YORP scattering torques on Gaussian random ellipsoids

1.  INTRODUCTION

In planetary sciences, rotational motion induced by interactions between solar system bodies and electromagnetic radiation is often attributed to the the Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect (Rubincam 2000). The YORP effect is related to anisotropic momentum exchange between the body and absorbed, reflected, or emitted photons relative to the body center of mass. For smaller particles, radiative torques (commonly referred to as RATs, see, e.g. Lazarian & Hoang, 2007) emerge from direct exchange of angular momentum in the scattering interaction. Further, RATs are considered to be strictly a result of scattering, and they provide a component of the total torque, which includes e.g., the accelerating and decelerating contributions of emissions. In the current work, contribution of emissions is omitted.

Using some simple scattering laws, such as the Lommel-Seeliger scattering law (see, e.g., Lumme & Bowell, 1981) allows relatively efficient treatment of torques due to scattering for non-convex bodies. Here, relative efficiency should be understood to correspond computational cost of calculation of disk-integrated brightness of non-convex bodies. A thermal emission part of YORP can be added in the future on top of the scattering code, as the bodies are essentially modeled as 3D meshes.

In the interactive poster, so-called YORP radiative torques, or YORP-RATs more concisely, are calculated and analysed for several test bodies. The non-interactive part of the poster describes the methodology and results of the work, the interactive part includes an online Jupyter script for participants of EPSC to work with.

 

2.  GAUSSIAN RANDOM ELLIPSOIDS

A Gaussian random ellipsoid (GRE) (Muinonen & Pieniluoma, 2011) is defined by its axis ratio a : b : c, and standard deviation σ and correlation length l, the two of which determine the statistics of the ellipsoid deformation. Each GRE can be identified by initializing a commonly available random number generator uniquely, e.g. the functions and their random number seeds in the random-library of NumPy (van der Walt et. al., 2011) version 1.18.4. Example of two similar GREs, deformed by different amount, are in Figure .

Figure 1. Gaussian random ellipsoids with with a : b : c = 1 : 0.8 : 0.5, l = 0.25, and σ = 0.05 (left) and 0.15 (right) initialized with a random seed 1 in NumPy.random.normal version 1.18.4.

 

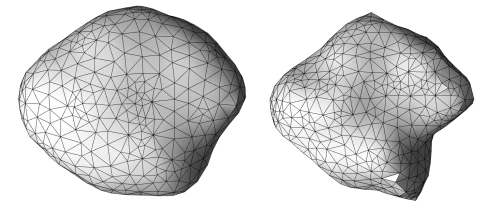
All GREs are generated as volume meshes, even though the YORP-RAT methodology only requires the definition of the body surface. The usage of volume mesh guarantees more accurate compatibility of the methodology with future addition of a model of thermal emission.

3.  YORP RADIATIVE TORQUES OF A DARK BODY

The Lommel-Seeliger law describes scattering from bodies with a low albedo, such as many asteroids and the Moon. The Lommel-Seeliger (LS) reflectance is defined as

 (1)

where ῶ is the single-scattering albedo, P(α) is the single-scattering phase function, μ₀= cos i of incident angle i, μ = cosϵ of emitted angle ϵ (both measured against the surface normal of an area element) and α is the common phase angle. The scattering of incient radiation produces radiation pressure, which for an irregular body is distributed unevenly across the surface, producing a net torque about the center of mass of the body. The total torque may be written as

 (2)

where the radiation pressure per area element is given by

 (3)

Above, Ω₊ is the hemisphere on top of an area element, 1_V is an indicator function of whether or not the area element is visible and illuminated, c is the speed of light and F₀ is the radiant flux density on the body surface.

When () is inserted into (), the Ω-integral may be computed analytically for the Lommel-Seeliger case. The integral corresponds to the so-called hemispherical albedo, and can be written as

 (4)

Altogether, it is most illuminating to work with a normalized total torque

 (5)

To analyse the YORP-RATs, the total torque must be solved as a function of the body orientation. We work in coordinates, where illumination is along the x-axis, and the observer is in the (x, z)-plane. In Figure , the orientation of the body axis is given by angles θ and ϕ, around which rotations fix the body orientation.

Figure 2. YORP scattering diagram used to analyse the radiative torques, or YORP-RATs.

 

4.  CONCLUSIONS

The final poster presentation will include an interactive script based on the theory above and extensive analysis of the properties of YORP-RATs.

REFERENCES

Hoang & Lazarian, 2008, MNRAS, 388, 117

Lazarian & Hoang, 2007, MNRAS, 378, 910

Lumme & Bowell, 1981, AJ, 86, 1694

Muinonen & Pieniluoma, 2011, JQSRT, 112, 1747

Rubincam, 2000, Icarus, 148, 2

van der Walt, Colbert, & Varoquaux. 2011, CSE, 13, 22