Effect of differential rotation on tidal waves in the convective envelope of low-mass stars and giant planets

Over 4000 exoplanets have been discovered in the past 25 years, most of which orbit around low-mass stars. For the shortest period exoplanets, like Hot-Jupiter systems, star-planet tidal interactions are likely to have played a major role in the orbital architecture and rotational evolution of the planets and their host star, through stellar and planetary tidal dissipation (see e.g. Ogilvie 2014, Mathis 2019, and references therein). Moreover, stellar tidal dissipation is known to vary considerably with the mass, age, rotation, and metallicity of the star (Mathis 2015, Gallet et al. 2017, Bolmont et al. 2017). To draw a comprehensive picture of tidal dissipation in stars and giant gaseous planets, one key physical mechanisms need to be further explored: differential rotation. Recent improvements in asterosismology and spectropolarimetry have helped to establish that the convective envelope of low-mass stars is differentially rotating like in the Sun (e.g. Barnes et al. 2017, Benomar et al. 2018). Similarly, data furnished by Cassini Grand Finale and the probe Juno, showed that cylindrical differential rotation extends into the convective envelope of Saturn and Jupiter below their surface (Galanti et al. 2019, Kaspi et al. 2017, respectively), which augurs similar rotation profiles for giant gaseous exoplanets.

 

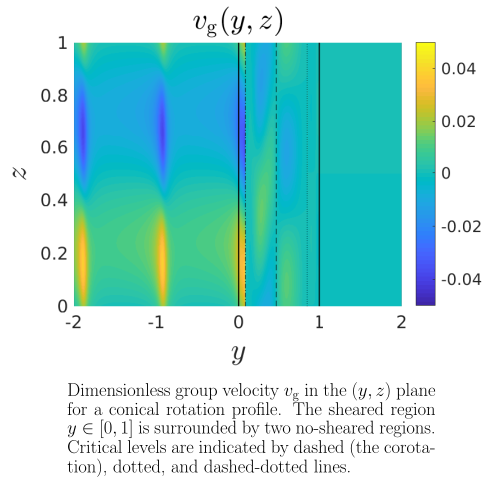
Nevertheless, differential rotation is rarely taken into account to compute tidal dissipation. Yet, Baruteau & Rieutord (2013) and Guenel et al. (2016a,2016b) have shown, using rotation profiles inspired by those encountered in solar-like stars and giant gaseous planets, that differential rotation can strongly affect the dynamics and dissipation properties of linear tidal waves. In particular, they pointed out that tidal waves deeply interact with zonal flows at the so-called corotation resonances, where the Doppler-shifted wave frequency vanishes, with the possibility that this interaction becomes unstable. This phenomenon that gives rise to an intense and localised energy dissipation is still poorly understood. In that context, we have developed a new local shear box that models a small patch of the convective zone of a low-mass star or a giant planet, in order to understand the complex interplay between tidal waves and zonal flows. The inclination of the box with respect to the rotation axis allows us to study the impact of cylindrical rotation profile when the box is at the pole (similar to Jupiter, Saturn and rapidly rotating stars rotation profiles, e.g. Gastine et al. 2013), and conical differential rotation profile when the box is tilted (analogous to that of the Sun and solar-type stars, e.g. Brun et al. 2017). We investigate the transmission of free linear inertial waves, within a fluid in thermal-wind balance, at corotation resonances and more broadly at critical levels that are singularities in the differential equation governing wave propagation. By the use of an invariant of energy flux, we diagnose each critical level according to the used rotation profile. Indeed, we find different regimes in which waves can be either fully transmitted, damped (as shown in the figures below) or even amplified with strong consequences for the tidal angular momentum exchanges. These different regimes of wave transmission are found both with conical and cylindrical rotation profiles, and depend on the critical level encountered, on the wave properties (direction, wavenumbers) and on the profile of the mean flow (first and second derivative). In particular, we demonstrate that a criterion analogous to the Miles-Howard theorem for the stability of gravity waves with vertical shear, is expected when using a cylindrical profile. Alongside this analytical study, we have numerically solved the leading equations for free inertial waves in a dissipative medium, where turbulent friction is taken into account thanks to a frictional damping force. We observed a good consistency between the analytical and numerical results, though some discrepancies are reported when using a non-linear mean flow profile at corotation. Based on these results, we discussed possible applications to the interiors of giant-gaseous planets and solar-like stars. Thanks to values of shear contrast given by asterosismology observations or 3D numerical simulations for solar-like stars, and to an analytical equatorial model for giant gaseous planets, we determine which regime of wave transmission is expected at each critical level in the convective envelope of these objects. It turns out that for K and G-type stars along their lifetime, and for Jupiter and Saturn at the present time, a regime where inertial waves are strongly damped is largely preferred in the convective envelope of these objects.