Poster presentations and abstracts
More than 10^7 kg of extraterrestrial objects or meteoroids ranging in size from a few microns to tens of meters in diameter enter the Earth’s atmosphere every year. A small fraction of these yields free samples of extraterrestrial matter - meteorites - for laboratory study. The majority, which burn up or ablate completely in the Earth’s atmosphere, appear as visible meteors in the night sky. Recording meteor activity and modelling the process of ablation allow us to measure directly the flux of small planetary impactors. This provides the 'ground truth' for estimating present cratering rates and planetary surface ages by implication.
The application of the latest observational and modeling techniques has rendered meteor science as one of the leading avenues for investigating the nature and origin of interplanetary matter and its parent bodies. This session will provide a forum for presenting fundamental results and novel ideas in this area and informing the broader planetary science community of the interdisciplinary impact of present and future work. In particular, it will solicit contributions related to planetary defense and the impact hazard from meter-sized asteroids.
Public information:
More than 10^7 kg of extraterrestrial objects or meteoroids ranging in size from a few microns to tens of meters in diameter enter the Earth’s atmosphere every year. A small fraction of these yields free samples of extraterrestrial matter - meteorites - for laboratory study. The majority, which burn up or ablate completely in the Earth’s atmosphere, appear as visible meteors in the night sky. Recording meteor activity and modelling the process of ablation allow us to measure directly the flux of small planetary impactors. This provides the 'ground truth' for estimating present cratering rates and planetary surface ages by implication.
The application of the latest observational and modeling techniques has rendered meteor science as one of the leading avenues for investigating the nature and origin of interplanetary matter and its parent bodies. This session will provide a forum for presenting fundamental results and novel ideas in this area and informing the broader planetary science community of the interdisciplinary impact of present and future work. In particular, it will solicit contributions related to planetary defense and the impact hazard from meter-sized asteroids.
Session assets
Introduction: On January 24th, 2016, 15:27 UTC, a bright daytime fireball was observed in Florida and registered by weather radar and a dash-board camera. Eight fusion-crusted stones with a total mass of 1.1 kg were found [1]. Osceola is now the 33rd meteorite (and the 9th L chondrite) with a published orbit [2].
Methods. Orbit. The atmospheric trajectory was reconstructed based on a dash-cam video recording with account for atmospheric conditions, using the methods described in [3,4]. The orbit (a=1.486 au; e=0.3406, i=13.20°, W=303.9°, w=169.0) was calculated based on this trajectory with the open source software Meteor Toolkit [5]. Noble gases. Four chips (total mass = 118.2 mg) were analyzed at ETH Zurich after problems were encountered during the analysis of the first two chips. Pending detailed analysis, we only report here the results for the second two chips (Os-3 and Os-4). Extraction was done by total fusion in a single temperature step (Table 1), and each measurement was bracketed by blanks. We measured 3,4He, 20,21,22Ne, 36,38,40Ar, 84Kr, 129,132Xe and some potentially interfering (isobaric) species [6]. We calculate meteoroid radius, shielding depth and cosmic-ray exposure (CRE) ages using [7,8] and the bulk chemistry for L chondrites given therein. Radiogenic gas retention (RGR) ages are based on typical abundances of 0.013, 0.043, 825 ppm adopted for U, Th, K, respectively [9]. Cosmogenic radionuclides. Results are forthcoming and will be presented and discussed at the conference.
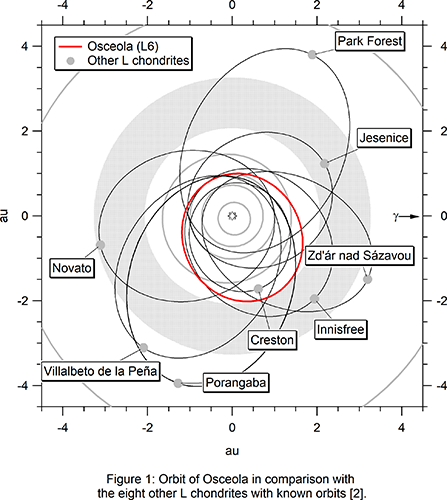
Results & Discussion. Orbit. The aphelion of Osceola’s barely Earth-crossing orbit is located just inside the inner edge of the asteroid belt, at ca. 2 au, i.e. the orbit is dynamically evolved (Figure 1). In that respect, it is comparable, among L chondrites, only to Creston [10]. Noble gas inventory. Unsurprising for an equilibrated L chondrite, the noble gases in Osceola are cosmogenic and radiogenic for He and Ne, with only minor trapped Ar, and Q-like 84Kr/36Ar, 132Xe/36Ar. Meteoroid size and cosmic history. The cosmogenic 22Ne/21Ne ratio of ~1.07 in both chips suggests irradiation in a meteoroid with a radius >50 cm, at a depth of >40 cm [7], consistent with the size estimate based on the fireball deceleration using the mass calculation method detailed in [11]. Under these shielding conditions, we expect a cosmogenic 3He/21Ne ratio of ~4.5, which fits well with the values measured in Os-3 and -4 (4.60 and 4.40), suggesting no significant loss of He relative to Ne during cosmic-ray exposure. Using 22Ne/21Ne-based production rates from [8], 3He and 21Ne in both chips give a consistent CRE age o 18±2 Ma, while 38Ar yields ~22 Ma. The former is our preferred age, since 38Ar can be more affected by sample inhomogeneities (i.e., distribution of Ca, which is the primary target for production of 38Ar) than 3He and 21Ne. This CRE age does not fall on any prominent peak in the CRE-age-histogram of the L chondrites (e.g., [12]). The CRE age is compatible with the expected collisional lifetime of a R >50 cm meteoroid in the asteroid belt (>14 Ma [13]). The U,Th-He retention age (4He corrected for the contribution of cosmogenic 4He = ~6 × 3He) of the two chips is 460 and 420 Ma, respectively, close to the age of the L chondrite parent body disruption event ca. 470 Ma ago [14]. Given the uncertainties inherent in these ages, it seems at least plausible that Osceola, like a large fraction of the L chondrites falling today, was affected by this shock event. The K-Ar retention ages for the two chips is are 1.5 and 1.1 Ga. The higher age from the K-Ar system might either be due to a contribution of atmospheric 40Ar (given that the measured 40Ar/36Ar ratios of the two chips are lower than the atmospheric value), or incomplete degassing of radiogenic 40Ar during the shock event 470 Ma ago. Dissimilar shock-degassing patterns for the U,Th-He and K-Ar systems are frequently observed for meteorites with shock stages S3 and S4 [15], consistent with the shock classification of Osceola of S4 [1].
Table 1: He, Ne, Ar in Osceola
| Chip (mg) | 3He=3Hecos | 4He | 20Ne | 21Ne | 22Ne | 36Ar | 38Ar | 40Ar = 40Arrad | 4Herad | 21Necos | 38Arcos |
| Os-3 (21.5) | 34.9 | 342 | 7.20 | 7.58 | 8.21 | 4.39 | 2.04 | 714 | 133 | 7.58 | 1.38 |
| Os-4 (15.8) | 35.9 | 337 | 7.00 | 8.18 | 8.73 | 3.55 | 2.11 | 498 | 122 | 8.18 | 1.64 |
References. [1] Bouvier et al., 2017, M&PS 52:2411. [2] www.meteoriteorbits.info, acc. 7.3.20. [3] Lyytinen & Gritsevich, 2016, Proc. Int. Meteor Conf., 159-163. [4] Lyytinen & Gritsevich, 2016, Planet. Space Sci. 120:35. [5] Dmitriev et al., 2015, Planet. Space Sci. 117:223. [6] Meier et al., 2017, M&PS 52:1561. [7] Leya & Masarik, 2009, M&PS 44:1061. [8] Dalcher et al., 2013, M&PS 48:1841. [9] Wasson & Kallemeyn, 1988, Phil. Trans. Roy. Soc. 325:535. [10] Jenniskens et al., 2019 M&PS 54:699. [11] Gritsevich, 2009, Adv. Space Res. 44:323. [12] Marti & Graf, 1992, Ann. Rev. Earth Planet. Sci. 20:221. [13] Farinella et al., 1998, Icarus 132:378. [14] Korochantseva et al., 2007 M&PS 42:113. [15] Stöffler et al., 1991 Geochim. Cosmochim. Acta 55:3845.
How to cite: Meier, M. M. M., Gritsevich, M., Welten, K. C., Lyytinen, E., Plant, A. A., Maden, C., and Busemann, H.: Orbit, Meteoroid Size and Cosmic History of the Osceola (L6) Meteorite, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-730, https://doi.org/10.5194/epsc2020-730, 2020.
Apollo-type asteroids Bennu and Ryugu are currently targets of sample-return missions. The goal of OSIRIS-REx mission (NASA) is to explore asteroid Bennu and Ryugu is being probed by JAXA’s Hayabusa2 mission. Observations of Bennu in January 2019 revealed ejecting material in the close proximity of the asteroid. Here we peresent our results of studying orbital evolution of potential meteoroid streams along the orbits of Bennu and Ryugu by integrating over 5000 test particles each for 1000 yr. We searched for their approaches to the Earth and we were also interested in evolution of their Earth MOIDs in order to estimate possible activity of potential meteor showers. Our results indicate possible observability from the Earth approximately for next 400 - 500 yr in both cases. Theoretical radiants for both asteroids and their potential meteor showers were also calculated.
How to cite: Kováčová, M., Nagy, R., Kornoš, L., and Tóth, J.: Bennu and Ryugu: Dynamical modelling of ejected particles to the Earth, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-659, https://doi.org/10.5194/epsc2020-659, 2020.
The InSight lander (Banerdt et al. 2020) on Mars is equipped with two cameras capable of sky imaging both of which have been used opportunistically to search for meteors. The rate of occurrence of Martian meteors has not been directly measured and initial reports of an imaged meteor by Selsis et al. 2005 were likely incorrect (Domokos et al. 2007). The meteor search is part of the investigation into the flux of impactors at Mars (Daubar et al. 2018).
The InSight cameras have been described by Maki et al. (2018). The Instrument Deployment Camera (IDC) can be aimed by a robotic arm and has a 45-degree square field of view (FOV). However, this camera was typically unavailable, and has only been used twice. The Instrument Context Camera (ICC) has a 120-degree fisheye FOV. It is aimed downward, but sees a broad section of the southern sky to around 20-degrees elevation angle.

IDC images are shown in Fig. 1. They were aimed to the southwest at an elevation of about 35 degrees, and on sols 126 and 176 (5 April and 27 May 2019), four 5-minute exposures were acquired. Stars are visible in the images, and will be used to determine the sensitivity. Many cosmic rays were seen (e.g., Fig. 2)—long ones can be mistaken for meteors, but they have a distinctive morphology with a narrow end and a diffuse end due to the charge diffusion process after the charged particles pass through the detector (Fisher-Levine and Nomerotski, 2015). Despite the Sun being 60 degrees down, diffuse sky brightness was visible (Banfield et al. 2020). No meteors were detected.

ICC images are shown in Fig. 3—about 75% of the images do not include sky. On 25 sols from 254 to 432 (15 August 2019 to 6 February 2020), the ICC acquired four, 5-minute exposures. No meteors were seen.
We will present an analysis of the results and their implication for the meteor rate at Mars. While no meteors were seen, the upper limit is likely to be constraining. Total exposure time is 540 minutes, using cameras more sensitive than the limiting exposures of Domokos et al. (2007) and with wider FOVs. However, the complex geometry and the time variable atmospheric dust extinction will be considered.

References. Banerdt et al. 2020. Nature Geoscience, 13, 183-189. Banfield et al. 2020. Nature Geoscience, 13, 190-198. Daubar et al. 2018. Space Science Rev. 214, 132. Domokos et al. 2007. Icarus 191, 141-150. Fisher-Levine and Nomerotski 2015. BNL-108381-2015-JA. Maki et al. 2018. Space Sci. Rev. 214, 105. Selsis et al. 2005. Nature 435, 581.
How to cite: Lemmon, M., Daubar, I., Banks, M., Vaubaillon, J., Sansom, E., and Maki, J.: The InSight Mars lander’s meteor search, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-499, https://doi.org/10.5194/epsc2020-499, 2020.
We introduce a new atmospheric refraction correction method which allows to retrieve fireball position with high accuracy without the need to consider at which distance from the observer or height above the Earth's surface the fireball is situated.
Traditional refraction correction is valid for objects positioned at infinite distance and it overcompensates when an object is situated inside the atmosphere. In this numerical study the overcompensated correction is reduced by artificially increasing the observing site height above the sea level, called the delta-z correction. We use analytically derived formula for the delta-z correction with different refraction models and compare these results to the numerical solution where light ray is traced through the atmosphere. Ray tracing technique is implemented on the finely meshed atmospheric layers in order to derive value of the correction.
We parametrize the viewing angle and the fireball height above sea level in order to define whether this delta-z correction is significant or negligible. Significance is defined by studying the errors caused by the observed horizontal altitude, height of the fireball above the sea-level, and height of the observing site. We find that the delta-z correction should be performed if a fireball is observed within 20 degrees altitude above the horizon or with negative altitudes. We also find that delta-z correction is always accurate if fireball is situated 20km or higher above the sea level and hence it can be safely applied in processing of all observational cases of fireballs.
How to cite: Visuri, J., Lyytinen, E., Sievinen, J., and Gritsevich, M.: Correcting the Atmospheric Refraction of Fireball Observations at Low Elevation Angles and Significance of the Correction, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-526, https://doi.org/10.5194/epsc2020-526, 2020.
An interesting new space-based data source for bolide detection has emerged within the past few years. Called the Geostationary Lightning Mapper (GLM) instrument, it resides aboard both National Oceanic and Atmospheric Administration (NOAA)'s Geostationary Operational Environmental Satellite (GOES) 16 and 17, and has been shown to be a legitimate detector of bolide events across the contiguous United States (Jenniskens et al. 2018). While it is clearly beneficial to be able to detect and verify bolide events using space-based remote sensing, the ability to use GLM data to build trajectory and orbital determinations for events would be an even greater advantage, as it would give us a uniquely independent view of the bolide event from space, and could add substantially to any pre-existing ground-based information available for the event. We will analyze light curves constructed from GLM data to find about fragmentation of these bodies, which might provide novel insights into the nature of the materials that comprise bolides and the physics behind fragmentation. We shall investigate these new avenues of approach-- orbit and trajectory calculations, and fragmentation analysis, both with GLM data.
Trajectory and orbit for these events will be calculated using publicly available Level 2 data. Level 2 data is produced by the application of a reduction pipeline to the raw sensor data (Level-0) which reduces noise and glint from the image, and geolocates pixels which satisfy a threshold condition. These instruments provide calibrated pixel intensity and location data for events occurring above the continental United States at or above -14 magnitude at a 500-Hz sampling rate in 20-second intervals (Jenniskens et al. 2018). Individually triggered pixels are labelled 'events', and a mass-weighted centroid is applied to get the 'group' data, which has sub-pixel accuracy. GLM data is released in NetCDF4 format with timestamped flash, group, and event position, in planetographic coordinates, and the calibrated luminous energy. With the stereo events, we can use line of sight to work out a trajectory. Orbit is calculated by using the velocity vector measured at the uppermost part of the luminous flight of the object. At the entry location, we calculate the heliocentric position and velocity vector and carry out backward time-integration using the open-source N-body software REBOUND (Rein and Liu 2012) to compute the position and velocity outside of Earth's Hill sphere.
We will investigate if GLM data provides greater insight into not just trajectory and orbit calculations, but also fragmentation analysis. It has been shown by Jenniskens et al. (2018) and Brown et al. (2019) that optical energy estimates can be reliably generated from GLM observations. We will attempt to show how the GLM data can be further utilized to assist in fragmentation analysis by modeling the light curve. Also, some of the events recorded by the GLM exhibit rapid fluctuations, or a "jitter" in the light curve just after peak intensity, which could be interpreted as a large-scale scattering of parent body material. This is further evidenced by multiple smaller events being seen by the sensor at different locations during the same time stamp. We have identified 42 such events and will continue to examine these unique light curves.
Ultimately, we investigate the extent to which GLM data can be used to get accurate trajectory and orbital calculations, in combination with ground based observations. We will highlight the importance of being able to verify trajectories with the Spalding Allsky Camera Network and will explore possible benefits of accessing Level 0 (L0) unfiltered non-centroided data from the GLM instruments in order to be able to calculate a more robust trajectory. We present preliminary results detailing the conditions under which a trajectory determination from GLM data is possible and fragmentation modeling of high-resolution events.
How to cite: Hughes, A., Sankar, R., Bamford, E., Gonzalez, M., Economon, S., Palotai, C., Free, D., and Longenbaugh, R.: Using the Geostationary Lightning Mapper data to calculate orbit and trajectory of bolide events and study fragmentation, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-467, https://doi.org/10.5194/epsc2020-467, 2020.
Abstract
Formula for the cumulative mass distribution of fragments of disrupted body, obtained as function of fragment mass, mass fraction of the largest fragment(s), number of largest fragments, and power index, is used to describe mass distribution of recovered meteorites for eight meteorite showers.
1. Introduction
To model independent motion and ablation of meteoroid fragments it is necessary to know their mass distribution. In this regard, an analogy can be drawn with impact experiments on high-velocity collisions, which were performed to simulate asteroid destruction. In many experiments [1, 2, and others] it was noted that cumulative mass distribution curve is well described by a power law. This is usually represented as cumulative number of fragments with masses larger than or equal to m is proportional to the power of m. This correlation between cumulative number of fragments and mass gives a linear plot in log–log coordinates with power index slope. It was also noted that whole mass distribution curve usually cannot be well represented by a single exponent in the power law and is divided into two or three segments with a steeper slope for larger fragments.
Here, the power law is used not for cumulative mass distribution, but for distribution of probability density. In this case, cumulative distribution is not a linear function of mass in log–log coordinates and enables to adequately describe results of impact experiments by single curve, i.e. using single exponent. We compare the proposed cumulative distribution with mass distributions of meteorites when a large number was collected.
Earlier, the power law distribution in discrete form was used for the grain mass distribution in studies of small meteoroids [3, 4, and others]. Different approaches were suggested to approximate mass distribution of found meteorites [5–7, and others].
2. Probability and cumulative distributions
We assume the power law for probability density function nm:
nm = Dm-β-1, nm = –dNm/dm. (1)
Here m is fragment mass, Nm is cumulative number of fragments with masses larger than or equal to m; exponent β is constant. Normalizing coefficient D is found using the equation of conservation of the total mass of fragments M (mass of the meteoroid just before breakup, mass of the target in experiments). Then probability density nm has a form (β < 1)
nm = M(1-β)/(ml1-β)m-β-1 . (2)
Here ml is mass of the largest fragment. Cumulative number of fragments Nm is found by integration of the second equation (1)
Nm = (1-β)/(βl1-β){(m/M)-β-l-β}+c. (3)
Here c is the number of largest fragments, l = ml/M is mass fraction of the largest fragment. Probability density nm (2) can be used to model meteoroid fragmentation; the total mass and energy deposition can be found by integration over all fragment initial masses.
3. Meteorite distributions
We test formula (3) by comparing with mass distributions of recovered meteorites for eight meteorite showers: Tsarev, Sikhote-Alin, Mbale, Bassikounou, Almahata Sitta, Košice, Sutter’s Mill, and Chelyabinsk. Comparisons show that formula (3) satisfactory describes meteorite mass distribution in cases of uniform change of fragment masses without gaps. The example of such distribution is shown in Figure 1. Asteroid 2008 TC3 entered the Earth’s atmosphere on October 7, 2008 and fragmented over the Nubian Desert in Northern Sudan; more than 662 meteorites were recovered, named Almahata Sitta [8]. We used data from tables [8] to construct the cumulative mass distribution of meteorites.
Figure 1: Almahata Sitta meteorites. Violet dots: data from catalog [8], red and green lines: formula (3) at β = 0.67 and 0.6; 662 fragments, M = 10.55 kg, ml = 0.379 kg.
Figure 2: Sutter’s Mill meteorites. Violet dots: data from table [9], red line: formula (3) at β = 0.5; 77 fragments, M = 942.7 g, ml= 204.6 g.
In cases where the largest fragment(s) is several times larger than the next one, formula (3) satisfactory describes meteorite mass distribution starting from the second one. Figure 2 shows the cumulative mass distribution of Sutter’s Mill (fall on April 22, 2012) meteorites, where mass of the largest fragment is almost 5 times that of the second. To construct the meteorites distribution we used data from table [9].
4. Summary and Conclusions
Formula (3) adequately describes cumulative distribution of recovered meteorites for considered meteorite showes. Difference between analytical and empirical distributions at very small masses is natural and should be, because, unlike laboratory experiments, it is problematic to find most small particles. Preliminary estimate of the most probable range of exponent β for meteorite distributions is from 0.5 to 0.7; further research is needed to determine more accurately the range of possible β values that could be used in probability density distribution for modelling meteoroid fragmentation.
Acknowledgements
This work was performed according to the plan of Institute of Mechanics of Lomonosov Moscow State University and was partially funded by Russian Foundation for Basic Research, grant 18-01-00740.
References
[1] Fujiwara A., Cerroni P., Davis D.R., et al. Experiments and scaling laws for catastrophic collisions. Asteroids II, 240–265. 1989.
[2] Holsapple K., Giblin I., Housen K., et al. Asteroid impacts: Laboratory experiments and scaling laws. Asteroids III, 1, 443–462. 2002.
[3] Campbell-Brown M.D., Koschny D. Model of the ablation of faint meteors. Astron. & Astroph. 418, 751–758. 2004.
[4] Borovička J., Spurný P, Koten P. Atmospheric deceleration and light curves of Draconid meteors and implications for the structure of cometary dust. Astron. & Astroph. 473, 661–672. 2007.
[5] Oddershede L., Meibom A., Bohr J. Scaling analysis of meteorite shower mass distributions. EPL 43, 598–604. 1998.
[6] Gritsevich M., Vinnikov V., Kohout T., Toth J., et al. A comprehensive study of distribution laws for the fragments of Košice meteorite. Meteorit. & Planet. Sci. 49, 328–345. 2014.
[7] Vinnikov V., Gritsevich M., Turchak L. Shape estimation for Košice, Almahata Sitta and Bassikounou meteoroids. Proceedings of the International Astronomical Union 10 (S306), 394–396. 2014.
[8] Shaddad M.H., Jenniskens P., Numan D., et al. The recovery of asteroid 2008 TC3. Meteorit. & Planet. Sci. 45, 1557–1589. 2010.
[9] Jenniskens P., Fries M.D., Yin Q.-Z., et al. Radar-Enabled Recovery of the Sutter’s Mill Meteorite, a Carbonaceous Chondrite Regolith Breccia. Science. 338. 1583. 2012. Supplementary Materials. https://science.sciencemag.org/cgi/content/full/338/6114/1583/DC1.
How to cite: Brykina, I. and Egorova, L.: Applying the formula for mass distribution of fragments of disrupted body to meteorite showers , Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-688, https://doi.org/10.5194/epsc2020-688, 2020.
Abstract
Models of meteoroid disruption into a cloud of fragments are considered: the two-parameter model, which takes into account changes in the cloud shape and density, and simple models without accounting these effects. Models are used to reproduce the energy deposition of the Chelyabinsk superbolide. Influence of ablation model is studied; for simple fragmentation models, optimal coefficient is proposed depending on heat transfer coefficient.
When meteoroid breaks up into a large number of fragments, at the first stage they move with a common shock wave, before dispersing enough distance to move independently. To simulate meteoroid disruption at this stage, models of a cloud of fragments moving as a single body were proposed and used [1–7, and others]. Such a cloud is flattened by pressure forces: it is compressed in a flight direction, and spreads out in a lateral direction. Fragment cloud models differ in equations for the rate of cloud lateral expansion. Comparison of models [3, 4] was made [7] for energy deposition modeling for the Chelyabinsk and Tunguska events. Here we consider two-parameter model [6], which takes into account changes in the fragment cloud shape and density, and simple models, for example [1, 4], without accounting these effects. We also consider the above models with limited midsection radius growth. We compare models as applied to reproducing the energy deposition of the Chelyabinsk superbolide. For correct comparison, we use them with the same ablation and drag coefficient models.
2. Fragmentation models
Spherical shape of meteoroid is assumed before breakup starts, then it continues its flight as cloud of fragments and vapor, moving as a single body, and sphere is transformed into spheroid with ratio of axes k. In model [6], in addition to flattening parameter k, parameter γ is introduced, characterizing decrease of fragmented meteoroid density δ due to increase of spacing between fragments: δ = δe/γ3 (γ ≤ 3), where δe is initial meteoroid density. Equation for the rate of increase of the fragment cloud midsection radius RS in two-parameter model [6] has a form:
dRs/dt = (γ3/k)1/2(ρ/δe)1/2V, k = 4πδeRS3/(3Mγ3), γ = (γm - 1)( ρ1/2 - ρf1/2)/(ρm1/2 - ρf1/2) (1)
Here t is time, ρ is atmospheric density, V and M are meteoroid velocity and mass; subscripts f and m correspond to values at heights of fragmentation start hf and maximum bolide brightness hm. Parameter γm is adjusted to match the observed height hm.
In simple models equation for the midsection radius RS is
dRs/dt = c(ρ/δe)1/2V, c = const (2)
Here c = 1 and c = (7/2)1/2 correspond to models [1, 5] and [4]. Simple models, in contrast to the two-parameter model, do not take into account decrease of density of disrupted meteoroid and change of its shape. Solution of equation (2) shows that midsection radius is determined only by initial parameters, ablation does not affect it, so fragmentation problem is separated from ablation and motion problem. For two-parameter model these problems are coupled.
3. Calculation results
We used various fragment cloud models to simulate interaction of the Chelyabinsk meteoroid with the atmosphere, solving ablation and motion equations together with equations (1), or (2), by Runge-Kutta method. Data [9] were used as initial parameters. Unknown entry mass was determined to match the observed maximum energy deposition [10]. For the drag coefficient we used: CD = 1.78 – 0.85/k. For the radiative heat transfer coefficient CH we used approximate formula depending on V, ρ, RS and k [6, 8]. Uncertainty parameter ψ is introduced in СН formula to account for effects of precursor, absorption by vapor layer, and other uncertain factors. Effect of CH coefficient on meteoroid mass loss, midsection radius, energy deposition, and entry mass estimate is studied by varying parameter ψ. Constant CH values are also used.
Figure 1: Energy deposition per unit height for two-parameter model (a) and models [1] (b) and [4] (c); black curve is observational data [10]; hf = 45 km.
Figure 1 shows that two-parameter model and simple model [1] enable satisfactory simulation of the observational energy deposition curve down to 27 km, respectively, at ψ = 1 (and СН = 0.1), and at ψ = 0.3 (and СН = 0.03). They give estimates of the Chelyabinsk meteoroid entry mass, close to estimates [9, 11]. Model [4] does not reproduce observational data. We found coefficient c in equation (2) for simple fragmentation models, which provides satisfactory agreement with observational data, depending on heat transfer coefficient. Two-parameter model gives much smaller increase of midsection radius than simple models. Limiting the midsection radius growth does not improve any models.
Acknowledgements
This work was performed according to the plan of Institute of Mechanics of Lomonosov Moscow State University and was partially funded by Russian Foundation for Basic Research, grant 18-01-00740.
References
[1] Grigoryan S.S. Motion and destruction of meteors in planetary atmospheres. Cosmic Research 17, 724–740. 1979.
[2] Melosh H.J. Atmospheric breakup of terrestrial impactors. Proc. Lunar Planet. Sci. 12A, 29–35. 1981.
[3] Chyba C.F., Thomas P.J., Zahnle K.J. The 1908 Tunguska explosion – Atmospheric disruption of a stony asteroid. Nature 361, 40–44. 1993.
[4] Hills J.G., Goda. M.P. The fragmentation of small asteroids in the atmosphere. Astronomical J. 105 (3), 1114–1144. 1993.
[5] Grigoryan S.S., Ibodov F.S., Ibadov S.I. Physical mechanism of Chelyabinsk superbolide explotion. Solar Syst. Res. 47, 268–274. 2013.
[6] Brykina I.G. Large meteoroid fragmentation: modeling the interaction of the Chelyabinsk meteoroid with the atmosphere. Solar Syst. Res. 52, 426–434. 2018.
[7] McMullan S., Collins G.S. Uncertainty Quantification in Continuous Fragmentation Airburst Models. Icarus 327, 19–35. 2019.
[8] Brykina I.G., Egorova L.A. Approximation formulas for the radiative heat flux at high velocities. Fluid Dyn. 54, 562–574. 2019.
[9] Borovička J., Spumy P., Brown P., et al. The trajectory, structure and origin of the Chelyabinsk asteroidal impactor. Nature 503, 235–237. 2013.
[10] Brown P.G. Assink J.D. Astiz L., et al. A 500-kiloton airburst over Chelyabinsk and an enhanced hazard from small impactors. Nature 503, 238–241. 2013.
[11] Popova O.P., Jenniskens P., Emel’yanenko V., et. al. Chelyabinsk Airburst, Damage Assessment, Meteorite Recovery, and Characterization. Science 342 (6162), 1069–1073. 2013.
How to cite: Brykina, I. and Bragin, M.: Comparative study of models of meteoroid disruption into a cloud of fragments, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1056, https://doi.org/10.5194/epsc2020-1056, 2020.
Please decide on your access
Please use the buttons below to download the presentation materials or to visit the external website where the presentation is linked. Regarding the external link, please note that Copernicus Meetings cannot accept any liability for the content and the website you will visit.
Forward to presentation link
You are going to open an external link to the presentation as indicated by the authors. Copernicus Meetings cannot accept any liability for the content and the website you will visit.
We are sorry, but presentations are only available for users who registered for the conference. Thank you.

