Dust Hazard Assessment using the Engineering Dust Coma Model of the Comet Interceptor mission

Introduction

The Comet Interceptor (CI) mission [1] will pass through a potentially hazardous region of a comet’s inner coma. It is therefore important to assess the dust impact risk to the spacecraft and their scientific instruments to aid hazard mitigation strategies. The purpose of the Engineering Dust Coma Model (EDCM) is to make predictions of which dust the three spacecraft will encounter during the active phase of the mission. The EDCM has been designed with a limited number of input parameters but keeping general physical realism of the phenomena in the inner coma.
We won’t know until after launch what the target comet of CI will look like. This is a particular problem for the dust coma because of the many parameters with unknown/unknowable values. The primary problem is thus not what model to use but what parameters to assume in a model of the inner dust coma. Because the different assumptions about the dust mass loss from cometary nuclei are strongly interdependent [2] it is not obvious a priori which set of parameters represent the best/worst case scenarios.
Instead of defining one set of parameters, we choose ranges for each parameter based on our knowledge of comets as e.g. Halley and other comets. All self-consistent combinations within those ranges will be run through our model to give a prediction of all possible coma environments within parameter space. This ensemble of dust environments is subsequently statistically evaluated to determine a probabilistic distribution of possible conditions which the spacecraft might encounter.
The EDCM is composed of three parts:

• the dust dynamical model that calculates the spatial distribution of dust,
• the scaling model that determines the absolute scaling of the dust densities,
• the instrument model that extracts the number density encountered along the spacecraft trajectories and performs the probabilistic calculations.

 

The dust dynamical model

The dust dynamical model describes the dust distribution within a cometary coma up to 1000 nuclues radii (R_N). It uses a minimal number of parameters for the description of a cometary dust coma, while keeping it physically realistic. This model physically consistently takes into account the expanding nature and asymmetry of the gas coma (caused by the gas production modulated by solar radiation) and considers the dust dynamics driven by the gas drag force, nucleus gravity, and solar radiation pressure. A series of general assumptions were made to simplify the model:

• The nucleus shape is assumed to be spherical.
• The gas is assumed to be an ideal perfect gas.
• The dust does not influence the gas flow (i.e. no back-coupling of the dust to the gas flow)
• The gas coma is constituted of one single species, H₂O.
• There is no extended gas/dust source/sink in the coma.
• The dust particles are spherical.

For the underlying gas dynamics model, we used the results by [3] who have calculated the gas field by solving the Euler equations. The dust dynamics model used in the EDCM is presented in detail in [4].

 

The scaling model

To determine the absolute scaling of the dust densities we chose to determine the dust-to-gas ratio, χ, by calculating Afρ for each set of parameters following the approach described in [5]. The dust column density of an aperture of 20R N is calculated. For points outside the simulation domain (1000 RN) a 1/r² extrapolation is applied. The column densities are then convolved with a power law (n ∼ a^−β ) and converted into reflectance using the scattering model of [6] as shown in [2]. The reflectance can then be used to calculate the Afρ as explained in [7]. The absolute scaling χ can then be determined by linearly scaling the model Afρ to the desired Afρ. I.e. if the model Afρ = 100 cm then an actual coma with Afρ = 200 cm is achieved with χ = 2.

 

The instrument model

In the final step, having determined the absolute scaling, χ, we extract the number density encountered along the spacecraft trajectories for each combination within parameters space. Again, for points outside the simulation domain (1000 R_N) a 1/r² extrapolation of density is applied.

At each point along the trajectory, we calculated the median number of particles predicted by all model variations as well as the 5^th, 10^th, 25^th, 75^th, 90^th, and 95^th percentile. The results for four size bins are shown in Fig. 1. The shaded areas illustrate the variation in the predicted number of particles based on the variation of the input parameters. These ranges thus reflect to a large degree the uncertainty of our knowledge of the future target of CI. As the dust size increases the expected number of particles decreases but the uncertainty increases. Further, the spike in particles around the closest approach (CA) highlights that most particles are encountered very close to CA. E.g. from cometo-centric distances of 10,000 km to CA at 1,000 km the dust densities increase by roughly 2.5 orders of magnitude.

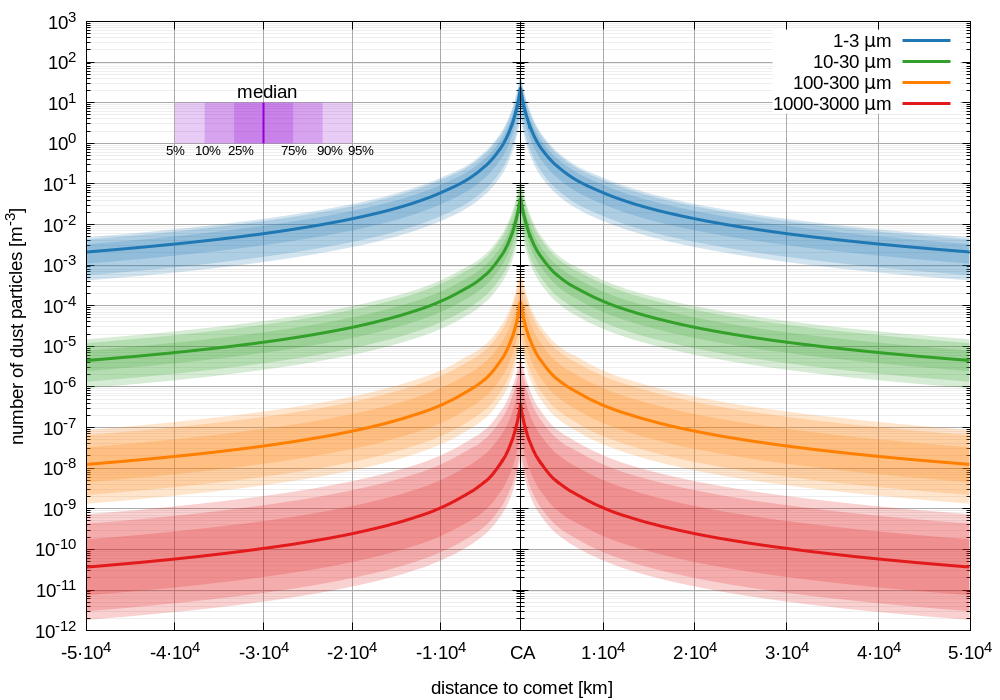
Figure 1: Number of dust particles along the spacecraft trajectory of spacecraft A as a function of cometo-centric distance. The shaded areas show different percentile ranges within which cases fall.

 

References
[1] Snodgrass & Jones (2019), Nature Communications, 10, 5418.
[2] Marschall et al. (2020), Frontiers in Physics, 8, 227.
[3] Zakharov et al. (2021), Icarus, 354, 114091.
[4] Zakharov et al. (2021), Icarus, 364, 114476.
[5] Marschall et al. (2016), A&A, 589, A90.
[6] Markkanen et al. (2018), Astrophysical Journal Letters, 868, L16.
[7] Gerig et al. (2018), Icarus, 311, 1.