TP3

Planetary collisions play an important role in the compositional and thermal evolution of planetary systems and such collisions are caracteristics of the final stage of planetary formation. The Moon-forming impact event is thought to (re)set the conditions for the subsequent thermochemical evolution of Earth and Moon. Large parts of proto-Earth are thought to melt as a consequence of the impact [e.g.1] and the extent of melting affects the evolution of the Earth’s interior and atmosphere. It is then critical to address the initial conditions of the proto-Earth and the volume and shape of a possible magma ocean after the impact. Previously, the Moon-forming giant impact was modeled with mesh-free so-called smoothed particle hydrodynamics (SPH [1, 2, 3]). In this study, we, in contrast, carried out numerical simulations of the Moon-forming impact event considering different impact scenarios with the three-dimensional (3D) iSALE code [4, 5], that tends to be more accurate in the description of thermodynamics and shock waves than SPH simulations. We also compare simulation results from our iSALE code with SPH models for benchmarking ([1]) because SPH uses self-gravity, whereas iSALE uses central gravity. We vary the impact angle (15° to 90°) and impact velocities (12 to 20 km/s). In order to quantify the volume of impact-induced melt, we use the so-called peak-shock pressure approach (‘Tracer method’) that has been used in several modeling studies [6,7] and is described in more detail by [8].

The benchmark study shows a good agreement of the two different numerical approaches with respect to pressure evolution. However the production of a magma ocean show some differences that need to be further explored, with notably the effects of considering central gravity instead of self-gravity into iSALE 3D simulations.

Acknowledgments: We gratefully thank the iSALE developers, including Gareth Collins, Kai Wünnemann, Dirk Elbeshausen, Boris Ivanov and Jay Melosh and Thomas Davison for the development of the pysaleplot tool. We also thank the Deutsche Forschungsgemeinschaft (SFB-TRR 170, subproject C2 and C4) for funding.

References:[1] Nakajima M. and Stevenson D. J. (2015) EPSL, 427, 286-295. [2] Canup R. M. et al. (2013) ICARUS 222, 200-219. [3] Canup R, M. (2004) Science 338, 1052-1054. [4] Collins G. S. et al. (2004) Meteoritics & Planet. Sci., 39, 217-231. [5] Wünnemann K. (2006) ICARUS 180, 514-527. [6] Wünnemann K. et al. (2008) EPSL 269, 529-538. [7] Pierazzo et al. (1997) ICARUS 127, 408-423. [8] Manske L. et al. (2018) 49th LPSC, abstract# 2269.[11] Pierazzo and Melosh (1999) EPSL 165, 163-176

How to cite: Allibert, L., Güldemeister, N., Manske, L., Nakajima, M., and Wünnemann, K.: Numerical modeling of the thermal state of Earth after the Moon-forming impact event , Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-613, https://doi.org/10.5194/epsc2021-613, 2021.

Introduction: The origin of the relatively high concentration of highly siderophile elements in Earth’s mantle [1] is still debated. One possible explanation is the addition of iron rich cores of differentiated impactors during the late accretion phase [2]. Since Earth has most likely had a magma ocean during this period [3], a quantitative understanding of impacts into such targets is of pivotal interest. In particular the answer to the question whether the impactor core material breaks into droplets or remains mostly in one piece is key, since this greatly affects the metal-silicate equilibration and mixing in the magma ocean [4]. This topic has been examined by several experimental as well as numerical studies [5,6,7]. The latter include mesh-free methods like smoothed particle hydrodynamics (SPH [8,9]), which may suffer from insufficient resolution, as well as grid based approaches. To expand on previous studies with such grid based algorithms [7], we implemented a method to improve the resolution and tracking of small material fragments in the simulation. This approach lays the groundwork for detailed studies of the size-frequency distribution of impactor cores in dependency to the impact parameters (core size, impact velocity and angle), as well as target properties (depth, temperature, and viscosity of the magma ocean). In a next step our results can then be used as input for further models studying material mixing in a convecting magma ocean [10].

Methods: We performed simulations of asteroid impacts using the iSALE-2D shock physics code [11,12], utilizing an Euler grid. By adding Lagrangian tracers at defined position at the start of the simulation, more detailed tracking of the material flow is possible. However, the exact fate of the material has to be reconstructed from these tracers in a post processing step, like in the stretching ratio model in [7]. In addition, this approach neglects the fact that small fragments tend to be underresolved and, thus, their motion in the model may suffer from numerical artifacts.

To address these limitations, we developed a method to reduce numerical artifacts as well as improve the tracking of smaller material chunks in iSALE. To this end, we identify and analyze fragments of a chosen material type, in this case the material of the impactor core, in the whole numerical grid during each simulation step. Based on predefined criteria, for example looking at the shape of a fragment or the strain in its individual cells, we determine if each individual fragment is still sufficiently well resolved. If this is not the case, the fragment will be broken up or completely removed by replacing the impactor core material in its cells with that of the surrounding magma ocean matter. The removed mass and volume will be saved in the nearest tracer, which approximates the movement of the fragment based on the surrounding velocities. By effectively freezing mass and volume of a fragment in this way, artificial distortion caused by insufficient numerical resolution for such small fragments is prevented.

The setup of our simulations consists of a 200 km diameter dunite projectile with a 100 km iron core, impacting a dunite half space. The upper 900 km of this target behave purely hydrodynamically without strength or viscosity, approximating a magma ocean. The resolution is varied between 20 and 80 cells per projectile radius (cppr).

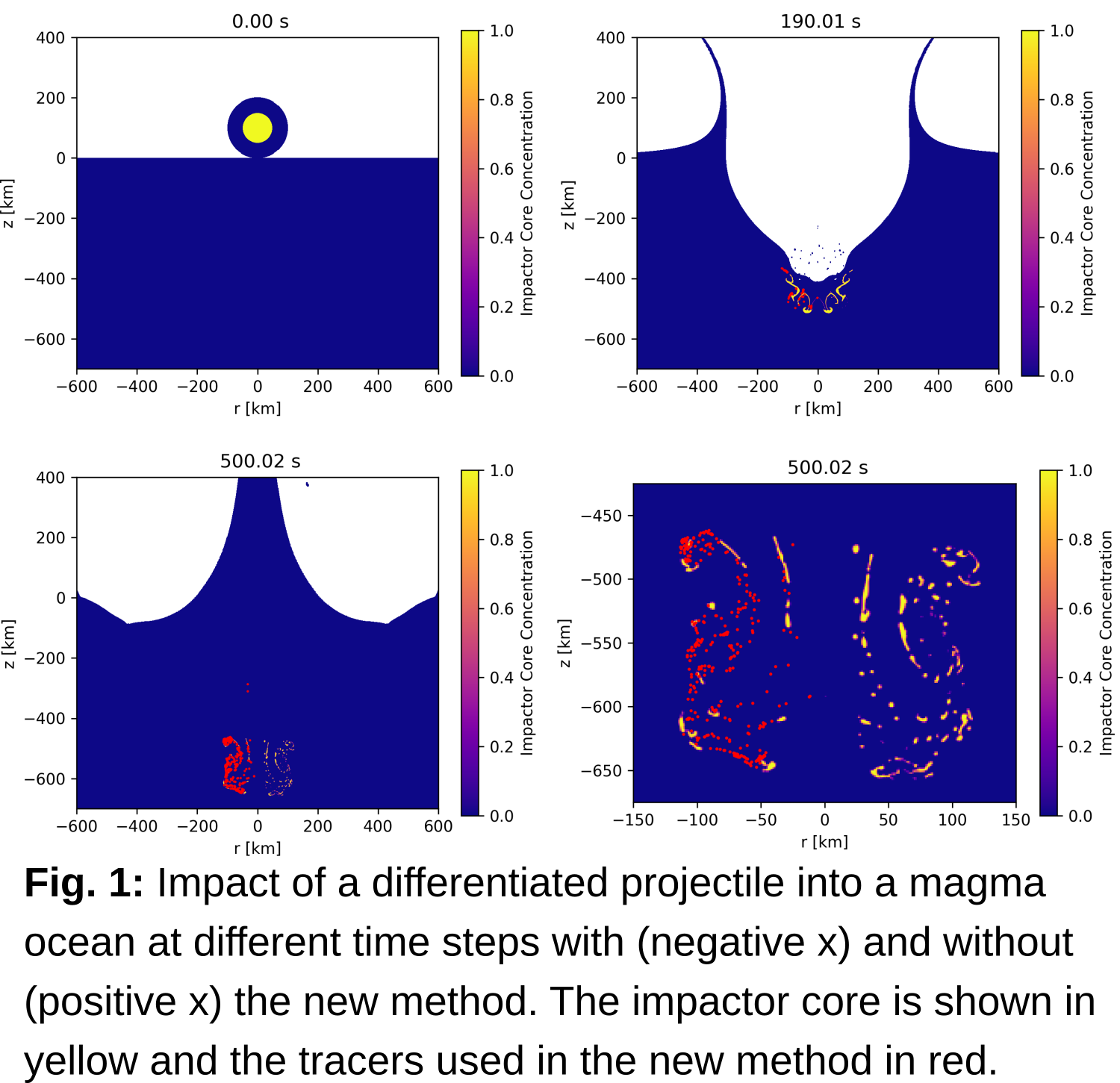
Results: Figure 1 shows a comparison between simulations with and without the new method for a cppr of 80 at different time steps. It shows the impactor core material (yellow) as well as the tracers used to save information in the method (red dots). The left side (negative x) of each image shows the results with the new method. It is clearly visible that, as impactor material penetrates deeper into the magma ocean, its core fragments into more and more pieces, the smallest of which are removed into tracers when using the method.

Discussion and Conclusion: The results obtained so far show that the impactor core breaks into many fragments during and after the impact, similar to observations in other studies [7]. The current criteria, based on the concentration in individual cells and their neighbors, as well as on a simplified approximation of the fragment shape, are not entirely sufficient to find all cases in which numerical artifacts occur. To achieve this, physical parameters like the strain inside the fragments have to be considered as well. It is also important to note that the current use of tracers to save the mass and volume of small fragments means that these cannot fragment further and that their interaction with other matter is strongly simplified - tracers follow the velocity field of the surrounding material. Some additional interaction will need to be implemented to evaluate how valid this approximation is.

Acknowledgements: We gratefully acknowledge the developers of iSALE-2D, including Gareth Collins, Kai Wünnemann, Dirk Elbeshausen, Tom Davison, Boris Ivanov and Jay Melosh. This work was funded by the Deutsche Forschungsgemeinschaft (SFB-TRR170, subproject C2 and C4).

References: [1] Walker R. J. (2009) Chem. Erde-Geochem. 69, 101-125. [2] Wood B. J. et al. (2006) Nature 441, 825-833. [3] Tonks W. B. et al. (1993) J. Geophys. Res. 98, 5319-5333. [4] Rubie D. C. et al. (2003) Earth Planet Sc. Lett. 205, 239-255. [5] Daguen R. et al. (2014) Earth Planet Sc. Lett. 391, 274-287. [6] Landeau M. et al. (2016) Nat. Geosci. 9, 786-789. [7] Kendall J. D. et al. (2016) Earth Planet Sc. Lett. 448 24-33. [8] Marchi S. et al. (2020) Sci. Adv. 6(7) eaay2338. [9] Monaghan J.J. (1992) Annu. Rev. Astron. Astrophys. 30, 543-574. [10] Maas C. et al. (2021) Earth Planet Sc. Lett. 554. [11] Collins. G. S. et al. (2004) Meteorics & Planet. Sci. 39, 217-231. [12] Wünnemann K. et al. (2006) Icarus 180, 514-527.

How to cite: Röhlen, R., Wünnemann, K., Allibert, L., Manske, L., Maas, C., and Hansen, U.: Core Fragmentation of Differentiated Bodies Upon Impacts Into Magma Oceans – Insights From Numerical Modelling, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-639, https://doi.org/10.5194/epsc2021-639, 2021.

The earliest atmospheres of rocky planets originate from extensive volatile release during magma ocean epochs that occur during assembly of the planet. These establish the initial distribution of the major volatile elements between different chemical reservoirs that subsequently evolve via geological cycles. Current theoretical techniques are limited in exploring the anticipated range of compositional and thermal scenarios of early planetary evolution. However, these are of prime importance to aid astronomical inferences on the environmental context and geological history of extrasolar planets. In order to advance the potential synergies between exoplanet observations and inferrences on the earliest history and climate state of the solar system terrestial planets, I will present a novel numerical framework that links an evolutionary, vertically-resolved model of the planetary silicate mantle with a radiative-convective model of the atmosphere. Numerical simulations using this framework illustrate the sensitive dependence of mantle crystallization and atmosphere build-up on volatile speciation and predict variations in atmospheric spectra with planet composition that may be detectable with future observations of exoplanets. Magma ocean thermal sequences fall into three general classes of primary atmospheric volatile with increasing cooling timescale: CO, N₂, and O₂ with minimal effect on heat flux, H₂O, CO₂, and CH₄ with intermediate influence, and H₂ with several orders of magnitude increase in solidification time and atmosphere vertical stratification. In addition to these time-resolved results, I will present a novel formulation and application of a multi-species moist-adiabat for condensable-rich magma ocean and archean earth analog atmospheres, and outline how the cooling of such atmospheres can lead to exotic climate states that provide testable predictions for terrestrial exoplanets.

How to cite: Lichtenberg, T., Graham, R. J., Boukrouche, R., and Pierrehumbert, R. T.: Coupled models of magma oceans and their primordial atmospheres: volatile speciation, cooling history, and impact of condensables, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-133, https://doi.org/10.5194/epsc2021-133, 2021.

We constructed a system of parameterized or semi-analytical representations of impact-related processes such as crater formation, atmospheric erosion, and melt production due to the direct effects of the impact as well as the long-term thermal effects triggered in the mantle by very large impacts in order to model how impactors of different types and a large range of sizes affect the CO₂-H₂O atmosphere and the interior of a terrestrial planet similar to Mars, Venus, or the early Earth. Mass fluxes of carbon dioxide and water between the impactor/outer space, the atmosphere, and the interior of the target planet are calculated in order to assess under which conditions atmospheres and interiors are depleted or enriched by processes related to impacts, melting/magmatism on different time scales, or weathering.

The impactor flux onto a planetary target is a stochastic process in terms of time, magnitude and location, which we describe with a size-frequency distribution of impactors and a cratering chronology. The temporal aspect, in combination with the complexities of the various effects of a single impact, cause the evolution to depend on its own history. In the absence of unique information about the impact sequence of a target, the evolution should therefore not be uniquely determined by cratering statistics, and the possible paths are expected to vary within a certain range. Thus, we aim to deduce a range of evolutionary paths for the volatile content of the atmosphere and, within limits, of the interior.

We consider rocky S-type and icy-rocky C-type asteroids as well as comets, covering a range of impactor-target density contrasts from about 1/6 to about 4/5 as well as a range of (absolute) impact velocities from a little less than 10 to almost 65 km/s. Impactor size ranges from 1 m to half the planetary radius. Atmospheric (surface) densities cover almost five orders of magnitude, ranging from a few millibars (modern Mars) to 95 bar (modern Venus).

With regard to atmospheric effects, there is a fundamental distinction to be made between blast-producing and crater-forming impacts; the boundary that separates these two regimes is mostly defined by the deceleration of the impactor and its resistance to breakup under the ram pressure during its traversal of the atmosphere. The direct effects of the former leave the interior essentially unaffected and interact only with the atmosphere. We use the formalism by Svetsov (2007) to assess the bulk mass transfer and balance resulting from mechanical erosion of the atmosphere and the disintegration of the impactor and estimate the balance for the individual volatiles from estimates of the impactor composition. In crater-forming impacts, there are additional effects that need to be included. Ejecta can contribute to the mechanical erosion of the atmosphere (e.g., Shuvalov et al., 2014) and also produce layers of porous material with a large, reactive surface that can absorb CO₂ from the atmosphere by weathering in the long-term aftermath of an impact. Moreover, they produce a crater that opens up the interior to mass exchange with the atmosphere. A key process in this context is the production of impact melt, which can serve as a vehicle for volatiles between the atmosphere and the interior by either releasing or removing (by dissolution) CO₂ and water, depending mostly on the pressure conditions at the interface; generally outgassing is expected to be more common, but still these two volatiles may behave quite differently. We find that CO₂ is expelled from the melt much more easily than water and will therefore enter the atmosphere under all conditions considered, whereas water may be retained in the melt at high atmospheric pressures. In addition to these common effects, very large impacts cause perturbations at sublithospheric depths and implant local thermal anomalies into the mantle that subsequently turn into upwellings and can cause longer-term magmatism and the local degassing from the deep interior.

How to cite: Ruedas, T., Wünnemann, K., and Grenfell, J. L.: Temporal evolution of impact-atmosphere-interior interactions in terrestrial planets, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-496, https://doi.org/10.5194/epsc2021-496, 2021.

Introduction

During the early stages of lunar evolution, the large amount of heat available from the lunar forming impact led to extensive melting of the Moon’s silicate mantle giving rise to a magma ocean. The fractional crystallization of the latter resulted in an inhomogeneous mantle with cumulate layers of increasing density towards the surface, due to iron enrichment in the residual magma ocean [1]. Such an unstable density distribution is prone to overturn and sets the stage for the subsequent thermo-chemical history of the mantle. In particular, this initial stage can significantly affect mixing of mantle material and the partial melt production, as well as the melt composition during the later stages of lunar evolution. The melt composition is directly linked to the composition of lunar basalts, whose variability at the lunar surface indicates complex melting processes and the presence of various mantle reservoirs.

In this study we model the solid-state convection, mixing and partial melt production in the lunar mantle. We investigate the effects of an initially layered mantle as a consequence of the fractional crystallization of the lunar magma ocean. To this end, we combine geodynamical models using the mantle convection code GAIA with petrological calculations that provide information about the composition and structure at the end of lunar magma ocean (LMO) solidification.

While previous mantle convection studies investigated lunar mantle melting in a purely homogeneous mantle [2] or with a localized KREEP layer [3,4], here we combine petrological and geodynamical models to investigate the degree of heterogeneity that can be produced by melting and mixing an initially heterogeneous lunar mantle.

Petrological modeling

The petrological model computes the crystallization sequence of the LMO. For the calculations in the deeper part of the mantle we use FOXMTR, for the shallower part alphaMELTS, as this approach is in good agreement with experimental data for the whole solidification process. We assume fractional crystallization of a spherical shell with an initial thickness of 1350 km, and a bulk lunar mantle composition from [5].

During crystallization the temperature is lowered stepwise and all minerals (except plagioclase) are assumed to accumulate at the bottom of the LMO and equilibrate with the melt at the respective pressure conditions. Plagioclase is assumed to float to the surface and form anothoritic crust.

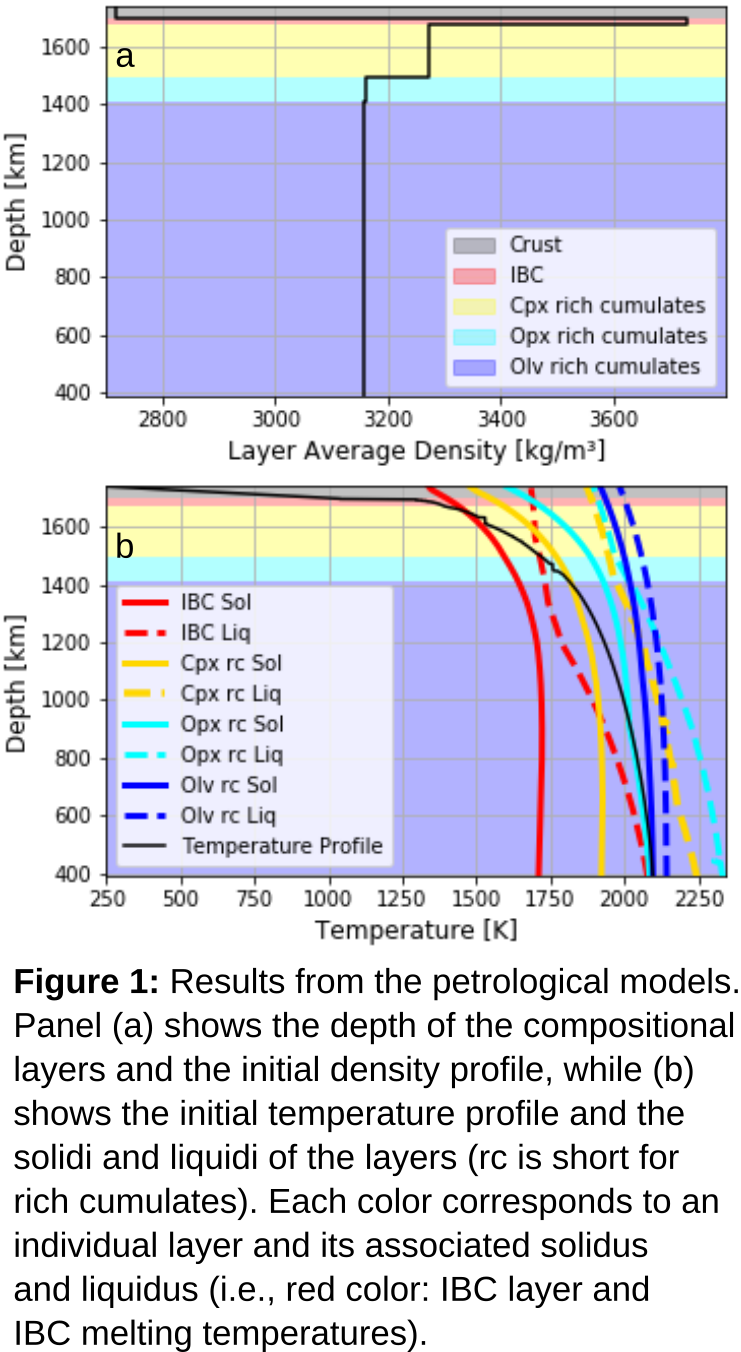
The resulting mantle structure is characterized by 5 compositional layers, where the predominant minerals are olivine, orthopyroxene, clinopyroxene, clinopyroxene and ilmenite (ilmenite bearing cumulates = IBC) and plagioclase (crust), respectively. For each of those layers an average density is calculated from the density profile after crystallization, as well as the change in density as a function of depletion. The solidus and liquidus temperature profiles are calculated for the average layer compositions using alphaMELTS.

The depths and densities of the compositional layers, the initial temperature profile, the solidus and liquidus profiles for each layer and the density-depletion functions of each layer composition are provided in the form of read-out tables.

The results from the petrological model are shown in figure 1. The densities of the mantle layers increase with radius due to the enrichment of iron in the melt during crystallization. The crust has a comparative low density (figure 1a).

The temperature profile follows the crystallization temperatures of the cumulates. In figure 1b the temperature profile is shown together with the individual layers and their corresponding solidi and liquidi. From olivine to IBC the solidus and liquidus temperatures decrease because of the crystallization sequence (figure 1b).

Geodynamical modelling

We use the mantle convection code GAIA [6] in a 2D quarter cylinder geometry to model the thermochemical evolution of the compositionally heterogeneous lunar mantle. The nondimensional conservation equations of mass, momentum, thermal energy, and composition are solved under the extended Boussinesq approximation. We use an Arrhenius law to calculate the temperature- and depth-dependent viscosity.

To track the composition of the mantle we use a particle-in-cell (PIC) method [7], where tracer particles carry information about material properties such as density, melting temperature, degree of depletion, amount of heat producing elements etc. Our models use between 35 to 50 particles per cell that are advected at each time step according to the velocity field.

In our simulations we account for core cooling and radioactive decay, as well as mechanical mixing. In addition, we consider the effects of melting by accounting for the latent heat during mantle melting, as well as solidus and density increase/decrease due to mantle depletion [8]. During melting, low melting point components are extracted from the mantle as the melt rises to the surface to form the basaltic crust. This leads to an increase of the solidus temperature requiring a higher temperature to further melt the residual mantle material. Gradual changes in density and solidus temperatures are extracted from the precomputed read-out tables of the petrological modelling.

Summary and Outlook

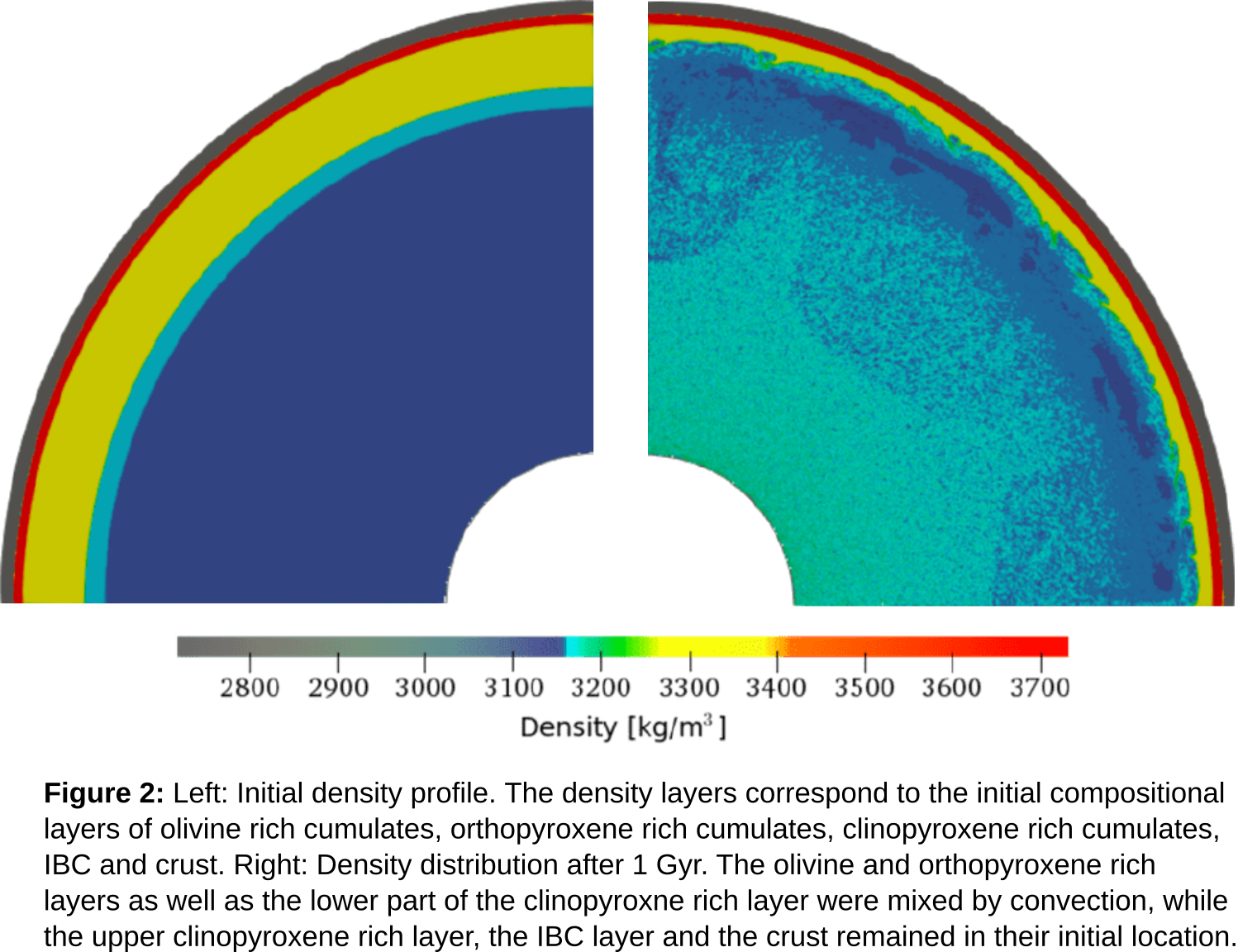
Our coupled petrological-geodynamical model of mantle convection and melt production will be used to investigate the thermochemical evolution of an initially heterogeneous lunar mantle structure (figure 2). Preliminary results show a smaller amount of melt produced in a heterogeneous mantle in comparison to a homogeneous one. We will present the distribution of the compositional layers as a function of time and compare the amount of melting produced from each individual component.

With this approach we aim to provide a link between melting processes in the interior of the Moon and the compositional diversity of basalts observed at the lunar surface. This in turn will help us to put constraints on the LMO crystallization and the subsequent thermochemical history of the Moon.

Acknowledgements

We thank Brian Doherty for his contribution to the numerical implementation.

I.B. and S.S. were supported by the German Research Foundation (Deutsche Forschungsgemeinschaft) SFB-TRR170, (subprojects C4 and A5).

References

[1] Elkins-Tanton et al., Annu. Rev. Earth Planet Sci. 2012; [2] Ziethe et al., PSS, 2009; [3] Laneuville et al., JGR, 2013 [4] Laneuville et al., JGR, 2018; [5] O’Neill et al., 1991; [6] Hüttig et al., PEPI, 2013; [7] Plesa et al., IGI Global, 2013; [8] Doherty et al., AGU, 2018.

How to cite: Bernt, I., Plesa, A.-C., Schwinger, S., Collinet, M., and Breuer, D.: Convection and melting in a heterogenous lunar mantle, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-834, https://doi.org/10.5194/epsc2021-834, 2021.

Introduction:

During its early history, the Moon experienced a phase of planetary-scale melting that is commonly referred to as the Lunar Magma Ocean (LMO). Progressive crystallization of the LMO lead to differentiation of the lunar interior into a crust and a stratified mantle.

The composition of the crystallizing solids strongly depends on the degree of crystal fractionation. However, the degree of crystal fractionation in the magma ocean and its evolution with time is still poorly constrained since it depends on multiple factors, including the initial thermal state of the LMO, the ability of the magma to suspend crystals by vigorous convection or the kinetics of crystal growth and dissolution during transport in the LMO and the resulting distribution of crystals in the LMO.

In this study we combine multiple modeling approaches to investigate the distribution of crystals in a solidifying magma ocean and the evolution of the crystal budget during LMO solidification.

Methods:

In our model we assumed that two processes contribute to the total crystal budget of the early LMO: the formation of crystals in regions where the temperature drops below the liquidus and the introduction of solid material by impacts.

Crystal formation in the LMO: We assumed an initially 1350 km deep LMO that progressively cools from its liquidus temperature. The thermochemical evolution of the solidifying LMO was modeled using the phase equilibria software packages alphaMELTS and SPICES [1,2,3]. The results were used to calculate the temperature and composition dependent viscosity of the evolving magma as well as the solidus and liquidus temperatures at different stages of LMO evolution.

We used the convection code GAIA [4] to model the temperature distribution in the convecting LMO at distinct stages of LMO evolution. We assumed that the time scale required for significant changes in the thermochemical properties is many orders of magnitude larger than the relaxation time of the convecting magma, so that the convection is in a steady state at any given stage of the LMO evolution. Therefore, we modeled each stage of the evolution separately, using the results from our solidification model to define the initial temperature profile and the physical properties of the LMO.

By comparing the steady state temperature distribution with the solidus and liquidus temperatures of the LMO, we determined the local equilibrium crystal fractions for each grid point.

Crystal introduction by impacts: We assumed that the LMO is impacted by a population of spherical impactors with varying initial sub-solidus temperatures of 0 K and 1360 K. As suggested by [5], we assume the size distribution of the impactor population to be that of a self-similar collision cascade and impactors to be of bulk Moon composition. The impact velocity was not considered as a model parameter and was assumed not to affect the properties and sinking behavior of the impactors.

Individual impactors were assumed to sink with velocities depending on their sizes and densities as well as the density and viscosity of the surrounding magma. This velocity and the LMO depth were used to calculate the residence time of the impactors in the LMO before reaching the LMO bottom.

We applied a 1D heat diffusion model to calculate the temperature distribution in the sinking impactor. Thereby we assumed time dependent boundary temperatures depending on the radial position of the impactor during sinking. Solidus and liquidus temperatures of the impactors as well as the latent heat of melting were calculated with alphaMELTS and used to calculate the degree of melting of the impactor.

Results:

We found that the temperatures in the early LMO are close to the mean temperature with deviations of only a few K due to vigorous convection. The local deviations from the mean temperature increase as the LMO evolves, since the liquid viscosity increases due to the compositional evolution and progressive cooling of the liquid.

Subliquidus temperatures are reached only within a region close to the LMO bottom. The thickness of this crystal bearing region decreases as the LMO solidifies.

Nevertheless, the shallower regions are not completely free of crystals due to the introduction of impacting material. Our results indicate that impactor fragments with a size of more than ~1m will reach the bottom of the LMO without melting completely.

Discussion:

The preliminary results of our models indicate that both the growth of crystals from the magma ocean liquid and the introduction of solid material from impacts contribute to the crystal budget of the LMO. This has implications for the magma ocean dynamics as the crystal budget influences magma viscosity.

The surface of impacting solid material reaching the crystallization region also provides nucleation sites that facilitate the heterogeneous nucleation of crystals. Heterogeneous nucleation on pre-existing solid aggregates requires less undercooling than homogeneous nucleation from the LMO liquid. Thus the presence of impacted material might lead to an increased average size of crystals or crystal aggregates in the LMO and hence facilitate the fractionation of solid material from the LMO.

To allow a quantitative estimate of the influence of impacts on the crystal budget in the early LMO, future iterations of the model will account for the effect of impactor fragmentation on the size distribution of sinking material, initial velocities of the fragments after impact and initial heating of the fragments by shock.

References:

[1] Smith and Asimow (2005), G³, 6.2.

[2] Davenport (2013), Planet. Sci Res. Disc. Report 1, 173.

[3] Schwinger and Breuer (2021), https://arxiv.org/abs/2104.06847.

[4] Hüttig et al. (2013), PEPI 220, 11-18.

[5] Perera et al. (2018), GJR: Planets, 123(5), 1168-1191.

How to cite: Wiesner, N. and Schwinger, S.: Crystal Distribution in a Solidifying Lunar Magma Ocean, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-548, https://doi.org/10.5194/epsc2021-548, 2021.

Introduction

The martian crustal dichotomy predominantly refers to the 4-8 km difference in elevation between the southern hemisphere and an apparent basin covering roughly 42% of the north, with this topographical picture being strongly reflected in distribution of crust below. Other associated features include a higher density of volcanoes and visible impact craters in the south relative to the north.

Most studies attempting to explain these properties have supported one of two theories; either the dichotomy formed solely through geodynamic processes [1], or a giant impact occurred that imprinted the crustal cavity in the northern hemisphere that is observed today [2]. Recent work has proved the importance of coupling these hypotheses, introducing a hybrid exogenic-endogenic scenario whereby a giant impact triggered a localized magma ocean and subsequent superplume in the southern hemisphere [3]. This has, however, only been investigated using a very limited range of initial parameters, all of which lead to significant heating deep into the mantle. This therefore motivates an interesting area of study – is there a sweet spot in the parameter space where hemispherically-thickened crust is the most likely outcome?

We aim to answer this question using a suite of smoothed-particle hydrodynamics (SPH) simulations, using the SPHLATCH code [3,4], that explore a large parameter-space chosen with the intention of limited internal heating. For the analysis of the simulation outcomes we apply a newly developed scheme to estimate the thickness and distribution of (newly formed or re-distributed) post-impact crust.

Method

The chosen initial parameters for the main suite of SPH simulations are as follows: impact angles of 0-90° in steps of 15°; impact velocities of 1.0, 1.2 and 1.4 times the mutual escape speed; impactor radii of 1000km, 1500km and 2000km; and relative core masses of 25% and 50%. All of these simulations use a resolution of 200,000 SPH particles, with near head-on collisions (0-30°) being modelled for 50 hours after impact and oblique collisions (45-90°) for 200 hours to allow for any secondary (or even tertiary) impacts.

Each model includes the effects of shear strength and plasticity (via a Drucker-Prager-like yield criterion) as such effects have been shown to be significant on the scales concerned in this study [3,4]. Moreover, the sophisticated equation of state ANEOS is being used along with a Mars-specific solidus [6] to accurately calculate the physical environment in which such solid characteristics must be considered.

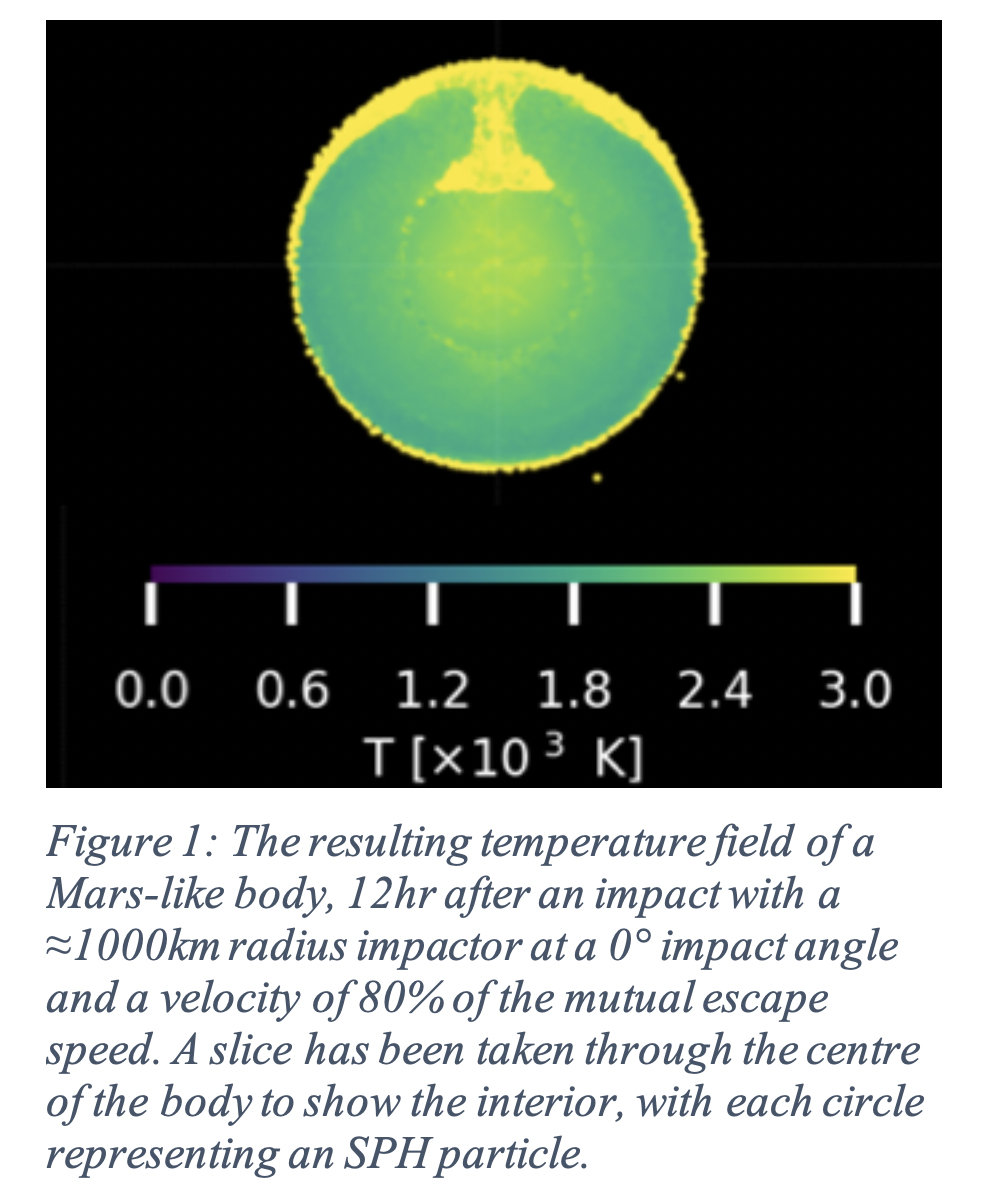
In all of these studies, both Mars and the impactor are treated as differentiated bodies composed of an iron core and a silicate mantle. An example result of one of these simulations can be seen in Figure 1.

Preliminary Results

The SPH kernel interpolation is used to convert the data of the simulations into high resolution, uniformly-spaced spherical grids. For each grid cell point we calculate a melt fraction using a simple linear relation involving the temperature, solidus temperature and liquidus temperature for the given pressure [7]. The Mars-specific solidus mentioned earlier is used for this purpose, along with a pressure-dependent peridotite liquidus [3,8] that has been modified to include the latent heat of melting. This then gives us a distribution of melt fraction throughout the entire mantle of our Mars-like body, as can be seen in Figure 2.

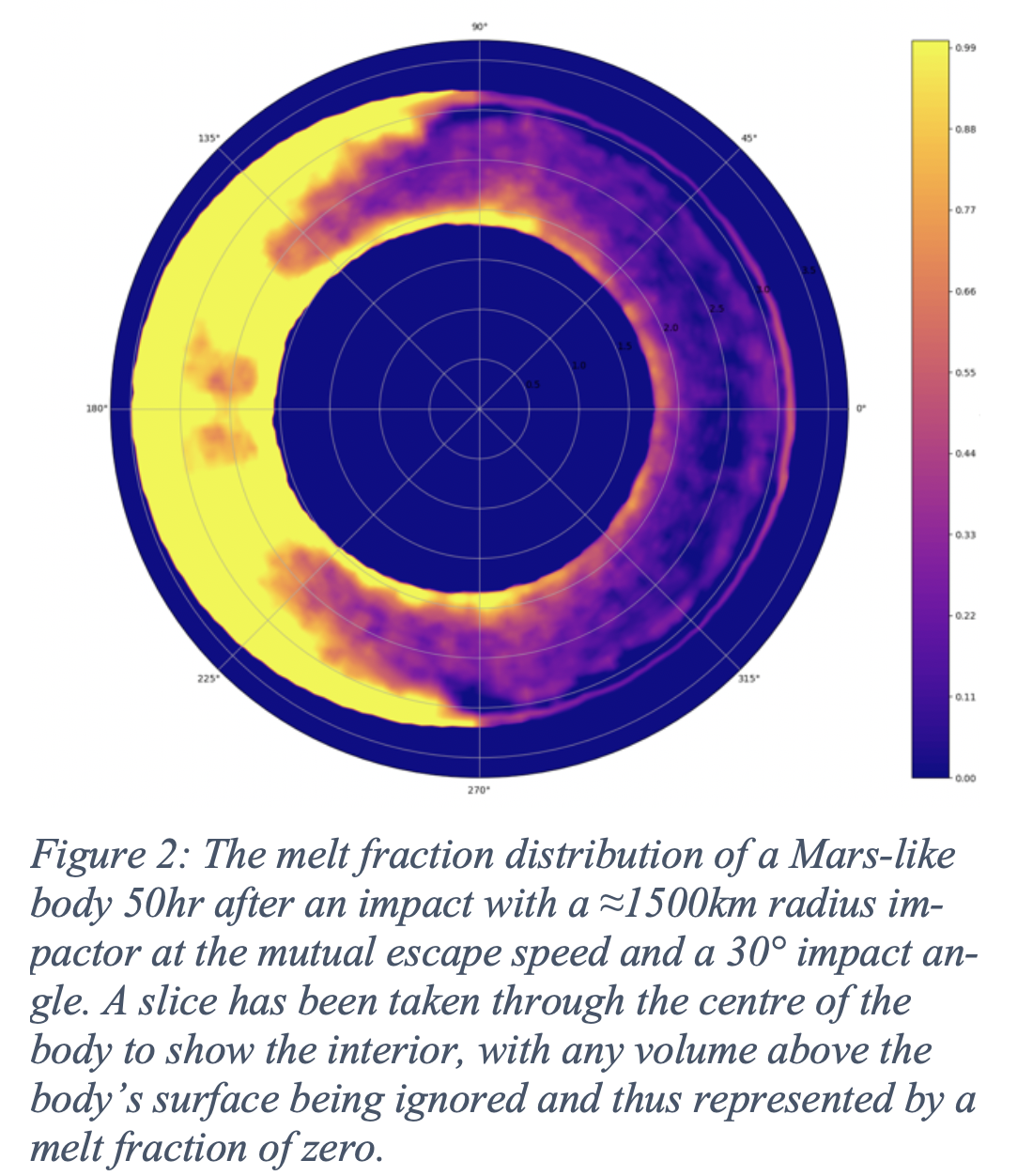
In order to estimate what fraction of this melt crystallises into basaltic to andesitic crust we use the pyroxene fraction of a fertile mantle: roughly 20% by mass [9]. In addition, any melt at pressures greater than approximately 7.4 GPa (equivalent to a neutral buoyancy depth of around 600km) [10] should become negatively buoyant and is therefore ignored in our crustal calculations. For each latitude and longitude coordinate on the grid, we can now find a total crustal mass and convert this to a thickness using a current estimate on the density of the martian crust [11]. This allows us to create maps of crustal thickness for each of our SPH simulations, an example of which can be seen in Figure 3.

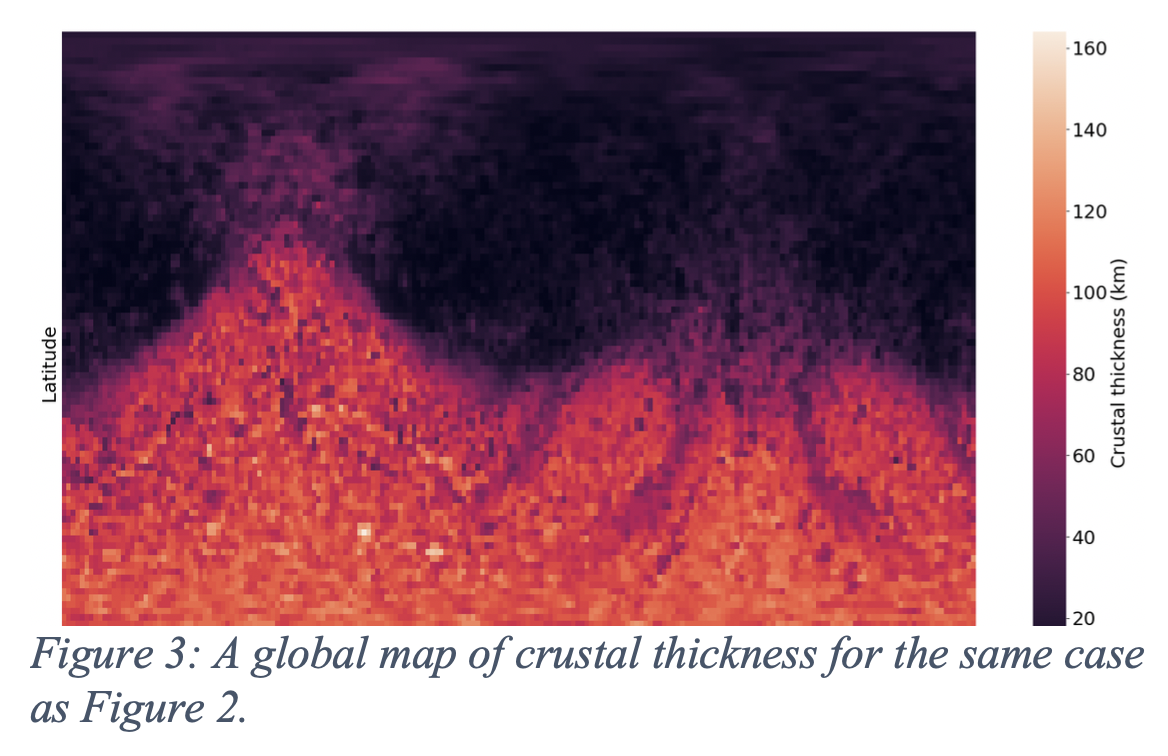
The initial results of this study have revealed promising hemispherical features in certain cases, with further analysis being made in an attempt to compare the results to those of the observational data in a quantitative manner (e.g. through bimodal fitting of crustal thickness histograms and spherical harmonics power spectra). In addition, the effects of a uniform, primordial crust being present on Mars before the dichotomy-forming event are being studied, as well as an investigation into the final distribution of the impactor material as this could be chemically distinct from the primordial martian composition.

Of notable interest are the results of the grazing impact angles, as some of the initial kinetic energy of the impactor is converted into rotational energy of Mars, allowing for subsequent merging events of decreased impact velocity. In addition, the effects of material strength have been found to be non-negligible, in contrast to previous beliefs that such aspects can be ignored on the length-scales involved in planetary collisions.

Acknowledgements

This project is supported by the Swiss National Science Foundation under grant 200021_175630.  We gratefully acknowledge the developers of the SPHLATCH code, including A. Reufer and A. Emsenhuber.

References

[1] Keller, T. and Tackley, P. J. (2009) Icarus, 202(2):429–443. [2] Marinova, M. M., Aharonson, O., and Asphaug, E. (2008) Nature, 453(7199):1216–1219. [3] Golabek, G. J., Emsenhuber, A., Jutzi, M., Asphaug, E. I., and Gerya, T. V. (2018) Icarus, 301:235–246. [4] Emsenhuber, A., Jutzi, M., and Benz, W. (2018) Icarus, 301:247–257.  [5] Jutzi, M. and Asphaug, E. (2011) Nature, 476(7358):69-72. [6] Duncan, M. S., Schmerr, N. C., Bertka, C. M., and Fei, Y. (2018) Geophysical Research Letters, 45:10, 211–10,220. [7] Burg, J.-P., Gerya, T.V., (2005) J. Metamorp. Geol., 23:75–95.  [8] Wade, J. , Wood, B.J. (2005) Sci. Lett., 236:78–95. [9] McKenzie, D., Bickle, M.J. (1988) J. Petrol., 29:625–679. [10] Breuer, D., Spohn, T. (2006) Planet. Space Sci., 54:153–169. [11] Goossens, S. et al. (2017) Geophys. Res. Lett., 44:7686–7694.

How to cite: Ballantyne, H., Jutzi, M., and Golabek, G. J.: Identifying the Sweet Spot for an Impact-Induced Martian Dichotomy, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-765, https://doi.org/10.5194/epsc2021-765, 2021.

The thermal evolution of a planet is heavily dependent on the concentration of heat producing elements inside of its mantle. Since heat producing elements like ⁴⁰K, ²³²Th, and ²³⁸U are incompatible in the solid mantle, melting processes trigger a redistribution of these elements from the solid towards the melt. Because the melt has a lower density than the surrounding material, it rises towards the surface and takes the incompatible trace elements with it. This causes the mantle to be depleted and the surface to be enriched with heat producing elements, which has a big impact on the overall thermal evolution of a terrestrial planet.

With the help of partition coefficients, the redistribution of trace elements can be calculated. In the past, mantle evolution models relied on fixed experimental data to model the redistribution of trace elements, but since partition coefficients are heavily dependent on pressure, temperature, and composition (Fig. 1), calculating them for each P-T-X condition would generate much more exact results. Previous partitioning models from Blundy et al. (1995) [1] were able to parameterize a partitioning model up to approximately 4 GPa, but for mantle evolution models a partitioning model up to 12 GPa would be preferable. This is why, based on Blundy et al. (1995) [1], we created a new parameterization for sodium partitioning which is applicable between 4-12 GPa [2]. Based on Blundy et al. (2003) [3], we based a broader approach for trace element partitioning between clinopyroxene/melt on the sodium partitioning model. By inserting the partition coefficient calculations into a mantle evolution model (Fig. 2), it is now possible to trace the redistribution of heat producing elements based on pressure, temperature, and melt composition. With this, we are now able to model the thermal evolution (or more specifically the cooling) of the mantles and crust formation of Earth and Mars in much more detail than before.

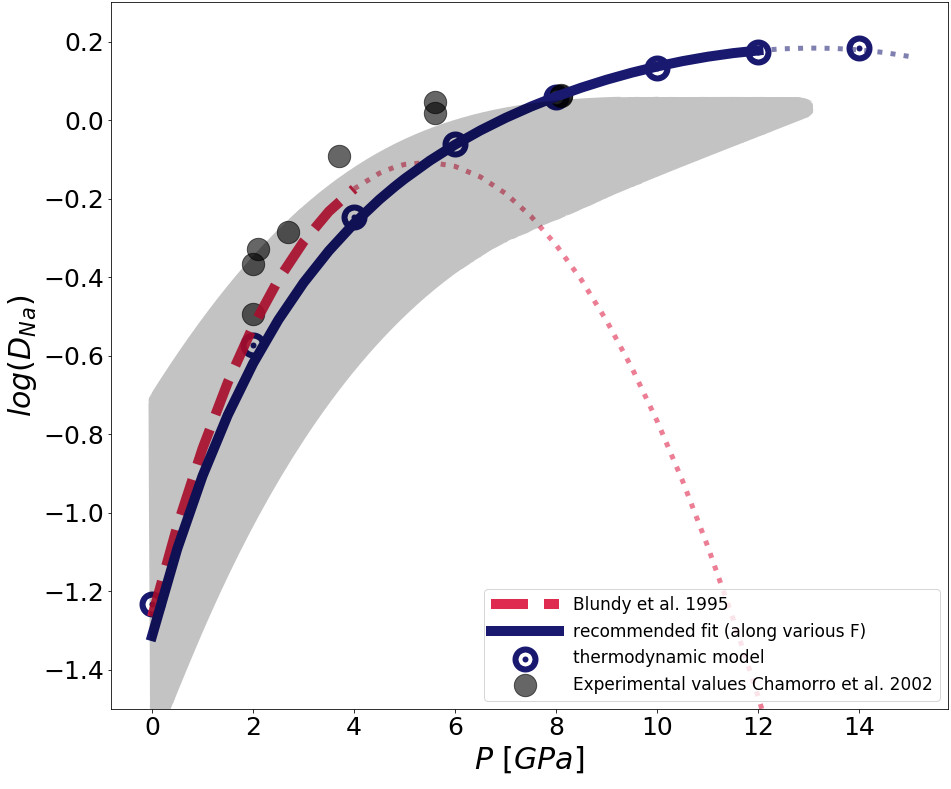
Fig. 1: The clinopyroxene/melt partition coefficient of Na parameterized to higher pressures. With increasing pressures, partition coefficients increase (see experimental data [4] (dots and shaded area). The model of Blundy et al. 1995 is applicable up to 4 GPa, while our model works best from 4 – 12 GPa (Schmidt and Noack, submitted).

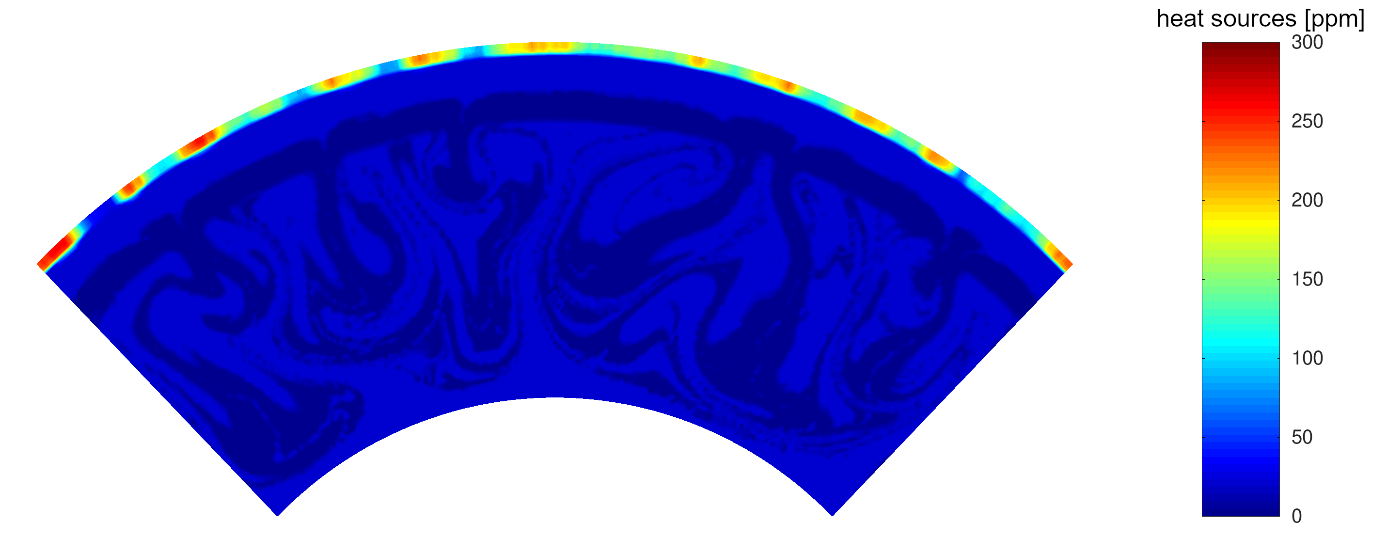
Fig. 2: Redistributed amount of the joint heat sources ⁴⁰K, ²³²Th, and ²³⁸U on Mars after 600 Myrs.

[1] Blundy, J.D., Falloon, T.J., Wood, B.J., and Dalton, J.A. (1995), J. Geophys. Res., 100, 15501-15515.

[2] Schmidt, J., Lena, N. (2021), IARIA, (submitted)

[3] Blundy, J.D. and Wood, B.J. (2003), RiMG, 52 (1), 59–123.

[4] Chamorro, E., Brooker, R., Wartho, J.-A., Wood, B., Kelley, S., Blundy, J. (2002), Geochimica et Cosmochimica Acta, 66 (3), 507-519.

How to cite: Schmidt, J. and Noack, L.: Thermal evolution and redistribution of trace elements inside the mantles of Earth and Mars, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-757, https://doi.org/10.5194/epsc2021-757, 2021.

The recent discovery of a terrestrial planet orbiting Proxima Centauri, our closest neighbor (an M5.5V star of 0.1 M_Sun mass and only 1.3 pc distance to the Sun), offers an excellent planet laboratory to study the most important theories of planet evolution and composition. The planet (Proxima b) is orbiting the star in its habitable zone at a separation of only ~0.05 AU and an orbital period of ~11 days, and most recent studies suggest a non-zero eccentricity of about 0.17. With a mass of >=1.2 M_Earth, Proxima b is expected to have a rocky composition, which might resemble the Earth. It is therefore an excellent target to characterize terrestrial planets similar to Earth, avoiding the inherent biases of only studying the terrestrial planets of the solar system.

Due to its close orbit and expected eccentricity, Proxima b most likely suffers from severe tidal heating, which can have an extreme incidence in the planet's habitability and the survival of an atmosphere. In this work, we perform a comprehensive analysis of the incidence that different distribution patterns of tidal heating can have on Proxima b's interior and thermal evolution. To accomplish this goal, we consider various possible geometries of the planet, from the simplest case, homogeneous distribution of the generated heat, to the more complicated cases, with an inhomogeneous distribution pattern that depends on the planet's interior structure (a stratified sphere, an incompressible homogeneous planet, or a two-layer structure with a differentiated core). The different models considered alter how tidal heat is distributed throughout the planet's interior, which can highly affect its overall thermal evolution.

Furthermore, due to its proximity to the central star, Proxima b may as well be in synchronous rotation with Proxima Centauri. This can cause an extreme surface temperature variation between the hemisphere that permanently faces the star and the opposite hemisphere. In this work, the effect that synchronous rotation may have on Proxima b's interior is also thoroughly investigated.

How to cite: Sanchis, E. and Noack, L.: Effects of tidal heating in Proxima Centauri b's thermal evolution, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-745, https://doi.org/10.5194/epsc2021-745, 2021.

Since the first exoplanet detection in 1992, the study of exoplanets has received considerable attention. It is becoming apparent that the diversity of the general exoplanet population extends beyond that of the Solar System and includes a variety of structures and compositions. For instance, recent research suggests that if a terrestrial planet forms with substantially more Al and Ca than Earth, it may be entirely rocky and lack a metallic core. Two such planets have been tentatively identified (Dorn et al., 2018).

Small-core and coreless planets are expected to differ significantly from Earth. Small cores may have fundamentally different dynamics compared to larger cores, which can affect the heat flow inside the planet and the generation and retention of a magnetic dynamo. Additionally, core size has been shown to affect the development of plate tectonics in numerical models (Osterloo et al. 2021; O'Neill et al., 2017), as well as carbon cycling on a planet. Investigating small-core and coreless planets therefore illustrates the potential diversity of exoplanets and offers insight into different regimes of mantle dynamics and plate tectonics.

In this study, we use the code StagYY (Tackley, 2008, 2013) to model the evolution of planets with core mass fractions ranging from 10^-1 to 10^-6 and compare them to an Earth-like reference model. We use mantle reference viscosities of 10²⁰, 10²¹, and 10²² Pa·s and crustal yield stresses of 30, 100, and 300 MPa. The planets are set to evolve for 4.5 Gyr.

In planets with smaller cores, hot plumes rising from the core-mantle boundary (CMB) are reduced in number and develop slowly compared to large-core planets. In the models with a reference viscosity of 10²¹ Pa·s and a crustal yield stress of 30 MPa, all planets show subduction and plate tectonic-like behavior. The onset of subduction is delayed in small-core planets compared to the Earth-like reference model. Basalt-enriched material accumulates at the CMB and forms a continuous layer in all planet models; this layer is thicker in small-core planets. Due to insulation by the basalt layer, CMB temperature is significantly higher in small-core planets at the end of the 4.5 Gyr evolution period.

For a lower reference viscosity of 10²⁰ Pa·s, subduction is initiated earlier and the basalt layer surrounding the CMB is thicker, while the reverse is true for the higher reference viscosity of 10²² Pa·s.

At higher yield stresses, some of the planet models undergo subduction and later transition to a stagnant-lid state. However, for a reference viscosity of 10²¹ Pa·s and a yield stress of 100 MPa, there is no consistent trend regarding this transition. For a yield stress of 300 MPa, planets with core fractions of 10^-3 and larger do not show any subduction, but remain in stagnant-lid state throughout the evolution period. In planets with smaller core fractions, subduction events occur starting at 2.5 Gyr. This agrees with previous research suggesting that a small core size can favor the initiation of plate tectonics (Osterloo et al. 2021; O'Neill et al., 2017). In such cases, core size may crucially influence a planet's habitability, since a large-core planet may lack the plate tectonics that are sometimes considered essential to efficient carbon cycling, while a small-core planet may lack the gravity or magnetic dynamo necessary to sustain life.

We conclude that core size influences the onset of subduction and plate tectonics on terrestrial planets, as well as their thermal evolution. Small-core planets tend to initiate subduction later than their large-core counterparts and can also be subject to interior heating due to the hot basalt layers insulating the core. For high crustal yield stresses, small-core planets are more likely to develop plate tectonics, while large-core planets remain in a stagnant-lid state. However, this tendency is not evident at yield stresses below 300 MPa. 

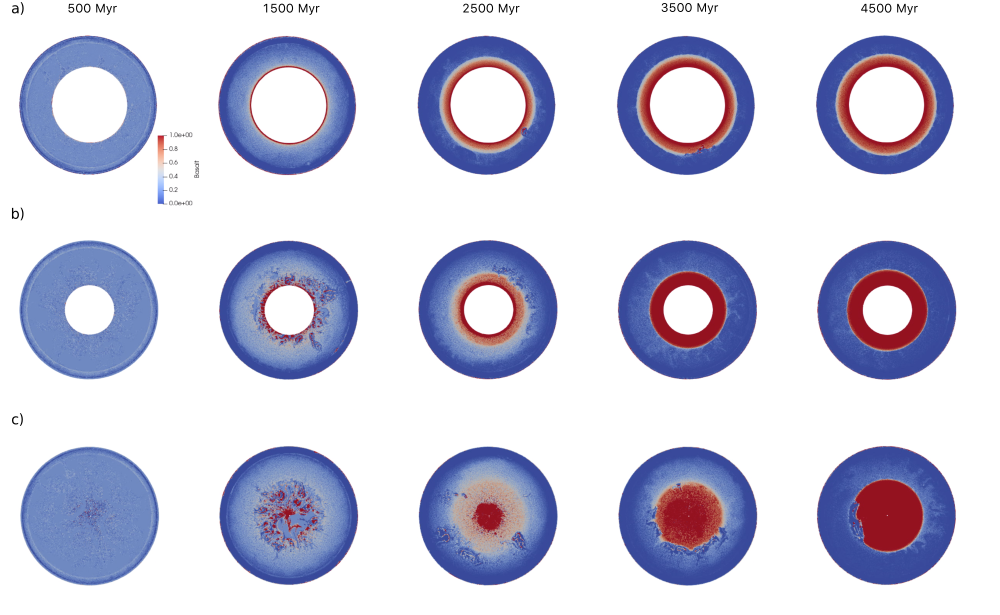
Figure 1: Interior differentiation of planets with a) Earth-like core size b) core mass fraction of 10^-1 c) core mass fraction of 10^-6 for a reference viscosity of 10²¹ Pa·s and crustal yield stress of 100 MPa.

References:

Dorn, C., Harrison, J. H. D., Bonsor, A. and Hands, T.O. A new class of Super-Earths formed from high-temperature condensates: HD219134 b,55 Cnc e, WASP-47 e, MNRAS, 484 (1), 712–727,  doi:10.1093/mnras/sty3435.url:http://dx.doi.org/10.1093/mnras/sty3435, 2018.

O'Neill, C., Lowman, J., Wasiliev, J. The effect of galactic chemical evolution on terrestrial exoplanet composition and tectonics, Icarus, 352, 114025, doi: 10.1016/j.icarus.2020.114025, 2020.

Oosterloo, M., Höning, D., Kamp, I. E. E., van der Tak, F. F. S. The role of planetary interior in the long-term evolution of atmospheric CO₂ on  Earth-like  exoplanets, A&A,  2021, doi:10.1051/0004-6361/202039664, 2021.

Tackley, P. J. Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid, Phys. Earth Planet. Inter, 171 (1-4), 7-18, doi: 10.1016/j.pepi.2008.08.005, 2008.

Tackley, P. J., Ammann, M., Brodholt, J. P., Dobson, D. P. and Valencia, D. Mantle dynamics in super-Earths: Post-perovskite rheology and self-regulation of viscosity, Icarus 225 (1), 50-61, doi:10.1016/j.icarus.2013.03.013, 2013. 

How to cite: Hasler, C. and Tackley, P.: Interior dynamics of small-core and coreless exoplanets, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-502, https://doi.org/10.5194/epsc2021-502, 2021.