Dynamic strength, fragmentation, and the impact cratering process

Introduction:  During impact cratering, target materials are subjected to extreme deformation conditions. Brittle deformation under these conditions, where strain rates can exceed 10¹ to 10² s^­­-1, is rate-sensitive. Typically, rocks are stronger when deformed at high strain-rate conditions [1]. This occurs because fracture propagation has a limited velocity; at high loading rates, the weakest flaws in a material are not able to cause failure before other, increasingly strong flaws are activated. This results in significant changes to mechanical properties and causes fragmentation of the target material [2, 3]. Dynamic compressive strength and fragmentation in brittle materials is not currently implemented in numerical impact simulations.

In this study, we present results of high strain rate mechanical tests to determine the characteristic strain rate for rate-dependent brittle failure and dynamic strength increase, and the fragment size and shape distributions that result from failure at these conditions. We investigated a variety of rock types and considered whether the fragment characteristics can be used as diagnostic indicators of loading conditions during brittle failure. In addition, we use numerical impact simulations to assess the significance of dynamic strength increase and compressive fragmentation during impact cratering at a variety of scales.

Methods: Mechanical data and samples were obtained using a hydraulic loading frame and a Split-Hopkinson Pressure Bar (SHPB). The hydraulic loading frame achieves strain rates from 10^-6 s^-1 to 10^-4 s^-1, while the SHPB achieves strain rates from 10¹ s^-1 to 10³ s^-1. As sample materials, we chose a variety of igneous, metamorphic, and sedimentary rocks in order to investigate differences between target types and material properties. From the mechanical experiments, the strain-rate dependency of strength was calculated and samples were generated for microstructural analysis. We focussed our microanalysis on the distributions of fragment size and fragment shape as functions of strain rate. Numerical impact simulations in this study were conducted using the iSALE shock physics code [4 and refs. therein].

Results:  We find that the characteristic strain rates of rocks, where the dynamic strength is twice the quasi-static strength, ranges between ~150 and ~350 s^-1 depending on lithology (Figure 1). Fragment size analysis demonstrates an inverse power-law relationship between fragment size and strain rate for dynamic failure under uniaxial compression. Unlike fragment size, we find that fragment shape is independent of strain rate under dynamic uniaxial loading (Figure 3).

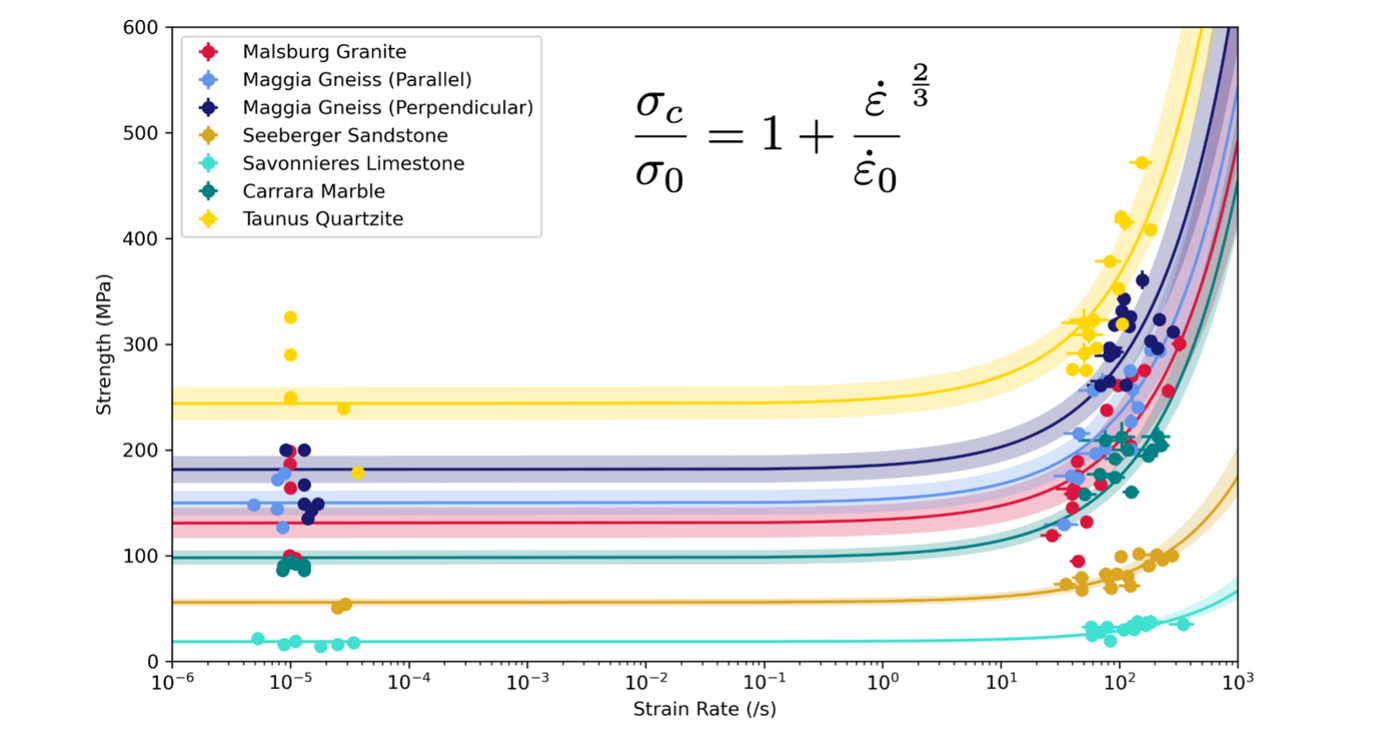
Figure 1. Rock strengths from quasi-static and dynamic testing. Each lithology follows the universal scaling relation (inset) of [1], where each material possesses a unique characteristic strength and characteristic strain rate. In all tested lithologies, strength dramatically increases at strain rates > ~10¹ s^-1. Data from [2, 3].

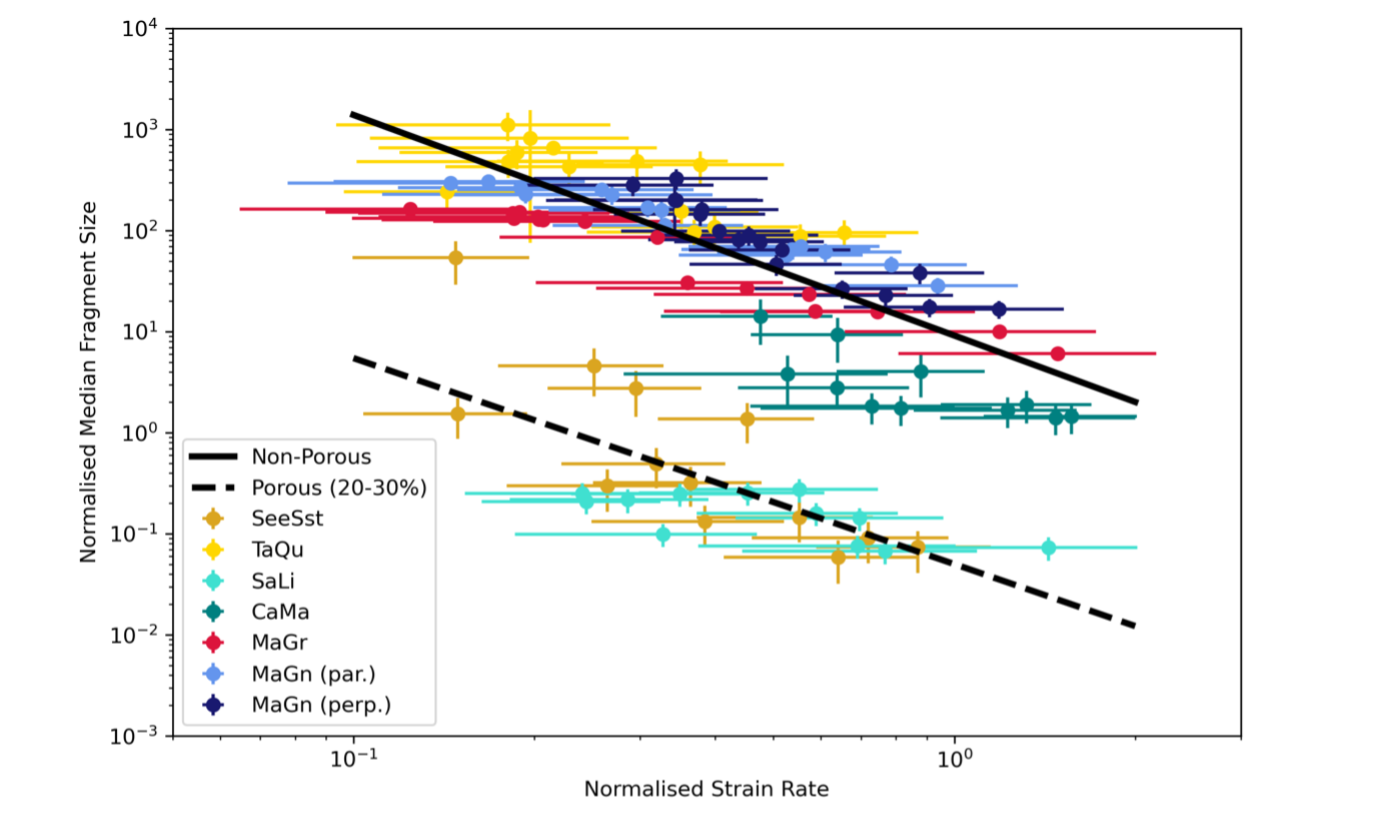
Figure 2. Scaled empirical fragmentation relationship for uniaxial compressive failure. The exponent of the relationship remains the same, while the constant varies between porous and non-porous rocks. From [3].

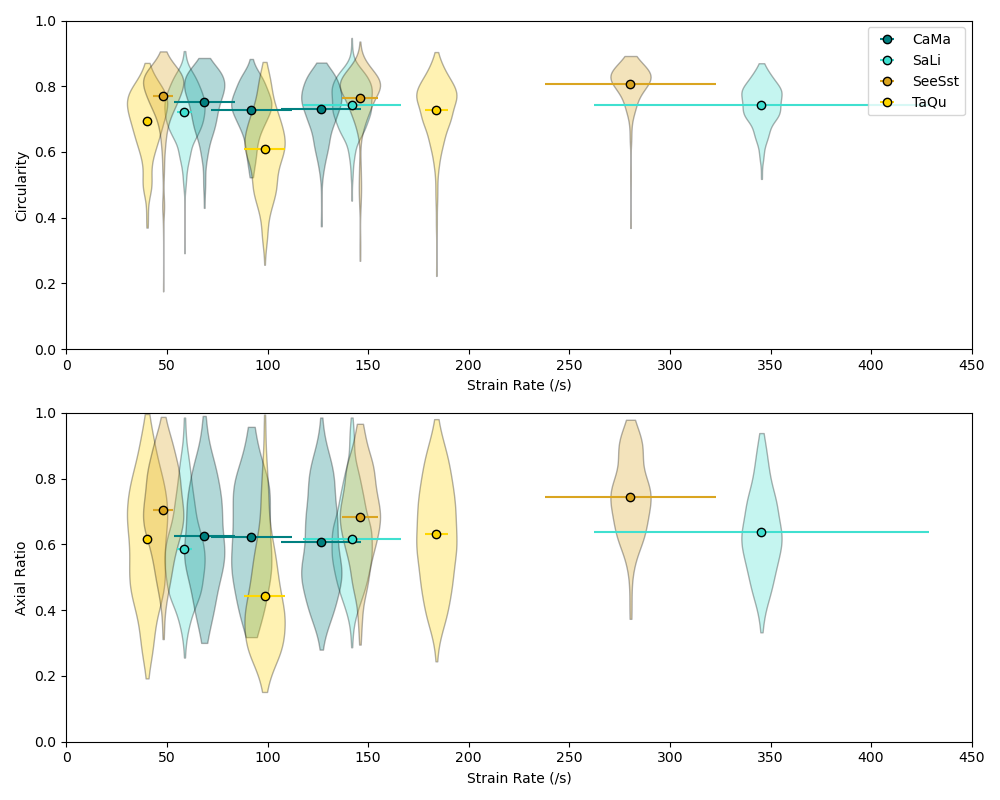
Figure 3. Fragment shape distributions for fragments > 2 mm as a function of strain rate. Distributions of fragment shape (circularity and axial ratio) for each sample are shown as kernel density estimates. Each point shows the mean shape parameter plotted against the strain rate, where the x-error bar shows the uncertainty in the strain rate. From [3].

Discussion: Numerical impact simulations demonstrate that strain rates are sufficiently high to produce rate-dependent effects in planetary impacts (v_i > ~5 km/s) where impactor diameters are ~100 m or smaller (Figure 4). Thus, rate-dependent strength and fragmentation plays an important role in small planetary impacts and laboratory impact experiments. Based on the results of this study, we are developing a semi-empirical approach to account for rate-dependent shear strength in numerical impact simulations (Figure 5); an important development due to the need to accurately ground-truth numerical impact models against laboratory scale experiments. Additionally, this study demonstrates that fragment size may be used as a diagnostic indicator of the strain rate at failure during impact loading while fragment shape cannot be used. However, our experiments only used uniaxial compressive loads, it is uncertain how truly triaxial stress states may affect fragmentation behaviour.

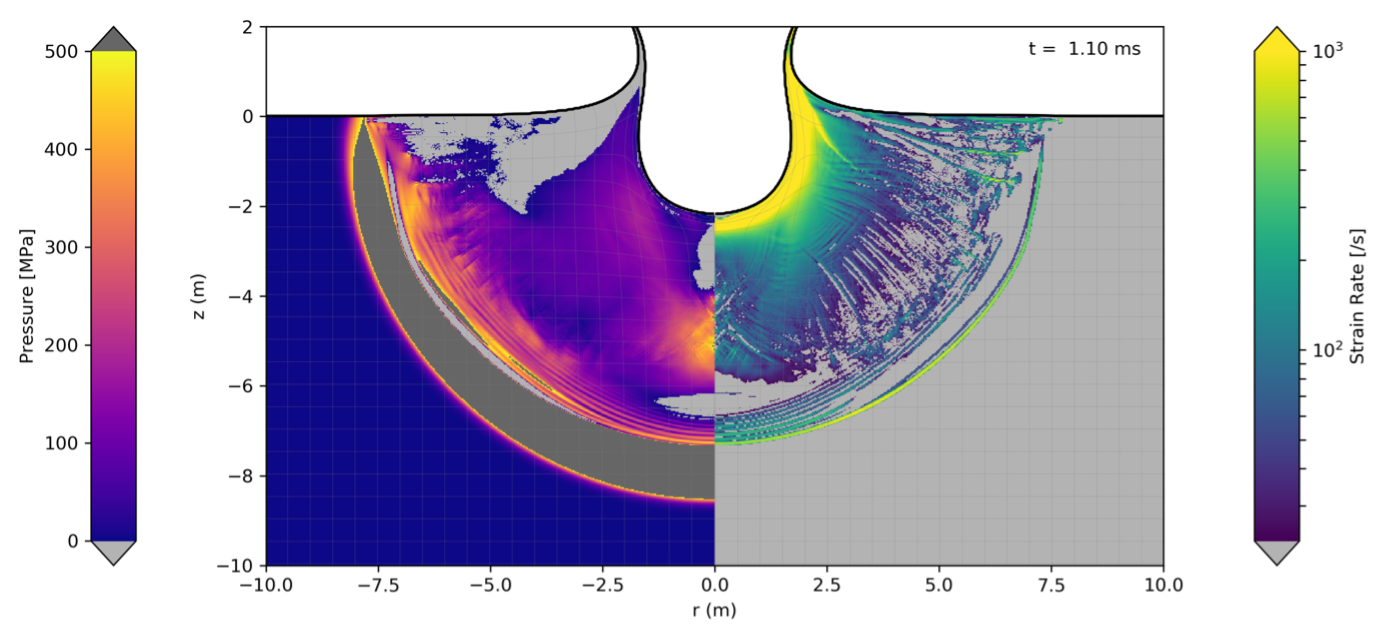
Figure 4. Crater excavation in an iSALE simulation of the impact of a 1 m diameter sphere at 15 km s^-1. Left) Coloured regions indicate pressures between 0 and 500 MPa, regions of tension are coloured light grey while regions of high confining pressure (e.g. within the shock wave) are coloured dark grey. Right) Coloured regions indicate strain rates greater than 22.5 s^-1, regions with lower strain rates are coloured light grey. Regions that are coloured in both panels are undergoing deformation in a regime where strength and fragmentation should be strongly controlled by strain rate. From [2].

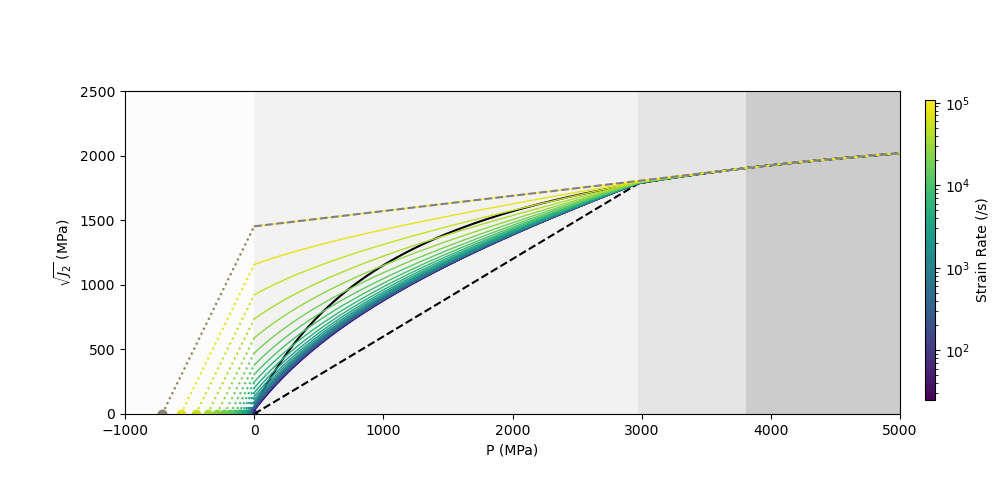
Figure 5. Implementation of dynamic strength as a modification of the ROCK strength model [5] (black). Uniaxial compressive and tensile strength follows the scaling law of [1]. In the high-pressure ductile regime (dark grey background shading), rock strength is not controlled by the behaviour of fractures, providing an upper limit for dynamic strength at ~10⁵ s^-1 [6] (grey).

Acknowledgments: H. Ickler and G. Mette are thanked for sample preparation. L. Müller, M. Dörffler, and T. Kern are thanked for lab assistance. The developers of iSALE are gratefully acknowledged. This work was funded by DFG Project KE 732/27-1.

References: [1] Kimberley, J. et al. (2013) Acta Materialia, 61:9, 3509-3521. [2] Rae, A. S. P. et al. (2020) JGR: Planets, 125:10. [3] Rae, A. S. P. et al. (2022) Tectonophysics, 824, 229221. [4] Wünnemann, K. et al. (2006) Icarus, 180:2, 514-527. [5] Collins, G. S. et al. (2004) MAPS, 39:2, 217-231. [6] Grady, D. E. (1998) Mechanics of Materials, 29:3-4, 181-203.