The crater-induced YORP effect

1. Introduction

The Yarkovsky–O'Keefe–Radzievskii–Paddack effect, or YORP effect, has influence on the rotational state and evolution of asteroids [1]. Depending on several parameters, it can either increase or decrease the spin rate as well as change the spin obliquity of an asteroid, on timescales that also depend on the physical and dynamical properties of the considered asteroid. 

The current YORP model reads

T_YORP = T_NYORP + T_TYORP,

where T_NYORP stands for the YORP effect on the whole asteroid and T_TYORP stands for the tangential YORP effect, which is related to the presence of boulders and surface roughness. 

Figure 1. The components on asteroids that contribute to the YORP effect.

The current model still faces difficulties calculating the YORP torque because of the extreme sensitivity of the YORP effect to the surface topology. Here, we consider the YORP effect of the crater, which has not been considered so far. We show that the crater-induced YORP (called CYORP hereafter) might contribute the total YORP torque as well, which adds a "CYORP" term into the Equation (1):

T_YORP = T_NYORP + T_TYORP + T_CYORP

with

T_CYORP = Σ_iT_CYORP,I

as a summation for a whole set of craters or concave structures on the asteroid (see Figure 1). The CYORP torque is the difference of the torque caused by the presence of the crater and the torque by the ground before the birth of the crater (dashed curves in Figure 1)

T_CYORP = T_crater - T_ground.

Using these calculations, we find that a single crater with a size equal to one-third of the asteroid size would produce a torque that is comparable to the normal YORP torque. The smaller craters also contribute to the total torque due to their large amount. Therefore, the CYORP should be considered in the future study of the YORP. The derived CYORP torque can be applied both for craters and for any concave structures on the surface of an asteroid, although a modification accounting for the geometry is needed. Since craters arise from collisions, this study builds a link between the rotational evolution and collisional history of asteroids.

 

2. Heat model

As a first step, we simply assume a non-thermal conductivity regime, which leads to a recoil thermal force on the surface element dS

f = -(2Φα/3c)dS.

where Φ and c are solar flux and light speed, respectively. Here α is the cosine of the angle between the surface normal vector and the light ray. 

 

3. Shape model for the crater

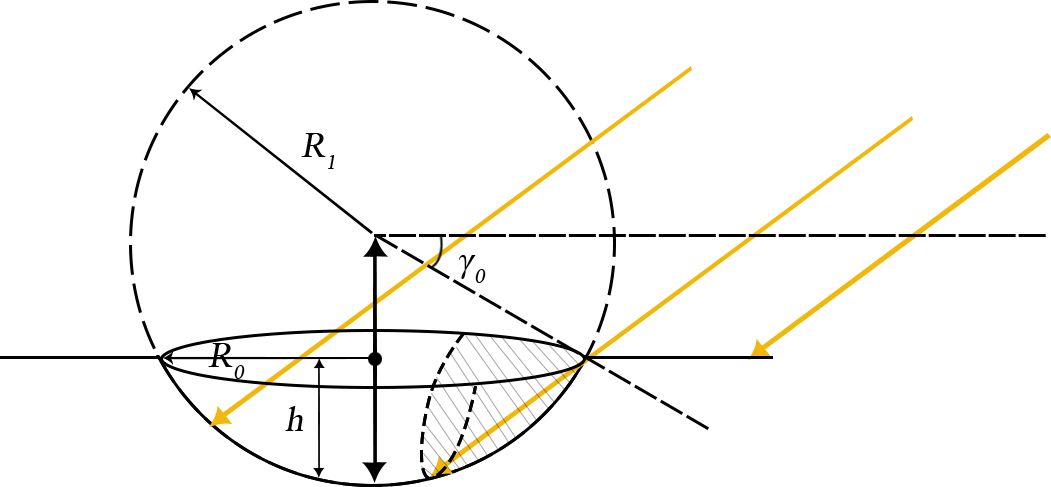
Figure 2. The shape model for the crater.

We consider a simple crater shape model, which is represented by a full or a portion of a semi-sphere with crater radius R₁ and depth h (see Figure 2). The widely used parameter depth d-diameter D₀ ratio expresses:

h/D₀ = (1-sinγ₀)/2.

Space mission data from real asteroids show that the average h/D₀ for fresh craters covers a range that goes from 0.11 (for Ceres) to 0.19 (for Eros), depending on many parameters and the considered crater diameter range [2].

 

4. Calculation of the torque

For a concave geometry such as a crater, the self-shadowing has a significant influence on the YORP effect. There are two major effects of self-shadowing. (1) During the rotational cycle, only a fraction of the crater is illuminated, depending on where it lies on the asteroid. (2) The effective recoil force is not normal due to the shelter. Considering non-zero thermal inertia and a given asteroid shape requires a numerical model and will be the topic of the next study.

The recoil force must be integrated over the whole illuminated area of the crater

F = ∫fdS.

The total torque of the crater is

T = ∫r×fdS ≈r₀×F.

Here r and r₀ are the position vector of the surface element on the crater and the sphere center of the crater, respectively. To understand this effect on the secular spin evolution of the asteroid, we need to average the torque over the orbital and spin motion.

In general, T_CYORP takes the form of the following scaling rule with the radius of the crater R₀ and of the asteroid R:
T_CYORP = gΦR₀² R/c,

where g is a function of the properties of the crater and asteroid, Φ is the solar flux and c is light speed.

 

5. Results and implications

We find that a single crater with a size equal to one-third of the asteroid size would produce a torque that is comparable to the normal YORP torque. This torque decreases with the crater as R₀². Since the cumulative size distribution of craters typically follows a power law of the form N(R ≥ R₀) ∝ R₀^-b, the larger number of smaller craters contributes also to the total YORP torque, although each of them causes a small torque. Moreover, since an asteroid experiences a lot of impacts leading to a crater during its evolution, the resulting CYORP torques may cause a random walk of the spin rate and obliquity of the asteroid, which may either slow down or even prevent the YORP spin up to occur. This can have strong implications on the formation of top shapes and binary systems based on this process [3], and on the resulting timescale, which will be assessed in future work.

 

Acknowledgment

We acknowledge support from the Universite Cote d'Azur. W.Z. and X.Y. acknowledge funding support from Chinese Scholarship Council. W.Z. acknowledge funding support from Origin Space Company. P.M. acknowledges funding support from the French space agency CNES and from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 870377 (project NEO-MAPP). 

 

[1] Rubincam, D (2000) Icarus 148, 2;

[2] Noguchi, R et al (2021) Icarus 354, 114016;

[3] Walsh, K and Jacobson, S (2015), in Asteroids IV (Michel et al., eds), UAP, 375.