Maximum dust-to-gas mass flux ratio in spherically expanding dusty-gas flow.

Maximum dust-to-gas mass flux ratio in spherically expanding dusty-gas flow.

In the context of an increasing number of complex multiparametric dusty-gas coma models it is convenient to address the analysis of complex physical phenomena in a step-by-step manner. We construct a set of elementary models with a minimum number of parameters selected to represent the key processes acting in a dusty gas coma. Such kind of models enables studies of generic processes occurring in variety of particular cases in order to reveal their characteristic features.

In many models of dusty-gas atmosphere of comets the dust-to-gas mass flux ratio is a free parameter. In order to constraint the range of possible values of this parameter, in the present work we propose an estimate of its maximum value. We consider a “pedagogic” case which assumes a homogeneous spherical nucleus and spherical expansion of dusty-gas (as an elementary model of the coma). The dust grains are assumed to be homogeneous spheres with size distribution given by a power law n(a_d) ∝ a_d^-β.

After ejection from the surface dust grain is accelerated by the gas flow in the gravitational field of the nucleus. In the present consideration we assume that the radiation pressure due to solar illumination of the grain is negligibly small. With increasing distance to the nucleus the gas drag and the nucleus gravitational attraction decrease and decoupling of gas and dust flows occurs at some distance. In absence of other forces, the dust grains continue motion with constant “terminal velocity”. As was shown in [1], the dust grains reach 90% of the terminal velocity at cometocentric distance about 6 comet radii.

The numerical integrated terminal velocity of dust grains in a spherically expanding flow is given in [1] for a wide range of conditions. The terminal velocity (v_d) can be approximated as:

v_d(a_d)/v_max=A_i Iv^Bi, i=1,2,3,

where Iv is a dimensionless parameter characterizing the efficiency of entrainment of the particle within the gas flow (see [1]), v_max is the theoretical maximal velocity of gas expansion, and A_i, B_i are coefficients of approximation defined for three non-overlapping ranges of parameter Iv variation.

To escape the gravitational attraction of the nucleus terminal velocity of the dust particles should exceed the escape velocity v_esc. This condition combined with the approximation for the terminal velocity allows us to derive the maximum size of the grains that reach escape velocity.

The dust mass loss rate q_d of grain size a_d and the gas production rate q_g are related via:

q_d(a_d)=χf_md(a_d) q_g da_d,

where χ=Q_d/q_g is the dust-to-gas mass loss rate, Q_d is the dust mass loss rate integrated over all grain sizes, and f_md is the normalized mass distribution of dust grains.  

Considering the foregoing, for the cometocentric distances greater than 6 comet radii it is easy to derive the energy fluxes of gas and dust flows.

The dust flow gets energy from the gas flow. Therefore, the maximum dust-to-gas mass loss rate corresponds a certain fraction of gas flow energy (κ<<1) being transferred in the dust flow energy.

In simplified form the expression for the maximum dust-to-gas mass loss rate is:

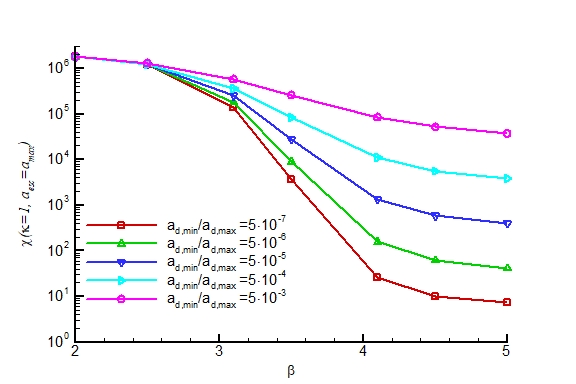
χ=κ(v_max/v_esc)² (a_max/a_esc)^4-β (3-β)/(4-β) [1-(a_min/a_max)^4-β]/[1-( a_min/a_esc)^3-β].

Fig.1 shows dust-to-gas mass flux ratio χ as a function of size distribution (β) for the case of a comet with nucleus radius R_n=1 km, mass M_n=10¹² kg, v_max=1 km/s, and κ=1. Note, that complete transfer of gas energy to the dust (κ=1) is not physically possible. In addition, in our reasoning it was assumed that the dust does not affect the gas flow, therefore the values of κ should be rather small. The Fig.1 shows that if the ejected dust has a broad range of sizes a_d,min/a_d,max (e.g. 5-6 orders of magnitude) and β>3.5, the maximum possible dust-to-gas loss rate is rather restricted. 

In our presentation, we show an extension of this approach to the more realistic multidimensional case as well. 

Acknowledgments

The work of N.Y.Bykov and A.V.Rodionov was supported by the Russian Science Foundation (grant No. 24-12-00299).

The work of A.Rotundi and V.Della Corte was supported by the Italian Space Agency (ASI) within the ASI-INAF agreements I/032/05/0, I/024/12/0 and 2020-4-HH.0. 

References

1. V.V. Zakharov, S.L. Ivanovski, J.-F. Crifo, V. Della Corte, A. Rotundi, M. Fulle. Asymptotics for spherical particle motion in a spherically expanding flow. Icarus 312 (2018)