Structure-dependent impact response propagation in residual rubble-pile asteroids after ejecta

Introduction: Kinetic impact deflection is one of the strategies for addressing the threat of near-Earth small body impacts. The DART mission has confirmed the effectiveness of deflection and demonstrated the generation and morphological evolution of ejecta. However, what happens to the remaining asteroid shortly after the impact remains a blind spot for in-situ detection. The propagation of residual kinetic energy within the remaining rubble-pile asteroid, and the possible internal structural damage, are crucial for understanding the subsequent evolution of the remaining asteroid. Using a proof-of-principle numerical model, we simulated the response within rubble-pile asteroids to residual impacts and found that the propagation strongly depends on the inherent internal stress chains. Such chains occur in three- and two-dimensional aggregates and we mainly study this phenomenon in 2D.

Methods: We first establish the 2D granular aggregate model and show the existence of initial stress chains based on the particle-scale stress tensor calculation^1–3. Velocity perturbations are applied in the form of pulses to particles in strong stress chains or weak stress regions, and then we observe the propagation of particle speeds, normal and shear stresses, and contact failure events. The dependences of propagation patterns on the magnitude and direction of perturbation velocity, the location of perturbed particles, and the particle size distribution of aggregates are investigated. All the numerical simulations are employed using discrete element code DEMBody^4–6.

Results: In bi-disperse granular aggregates (Fig. 1a), we observed that particle speed response preferentially propagates along the initial (pre-impact) stress chains than in the direction of perturbation velocity (Fig. 1b). The dynamic normal and shear stresses propagate faster and are higher along the inherent stress chain structure (Fig.1c). According to the probability scatter map in Fig.1d, particles under high dynamic shear stress are highly likely to have initially high stress levels, which means that they belong to initial stress chain structures. The heterogeneity of the initial stress chain structure causes anisotropy in the propagation of impact responses, as demonstrated by the D (it characterizes the mean propagating distance of particle speed response) evolution in the 8 sectors around disturbed particle I (Fig. 2).

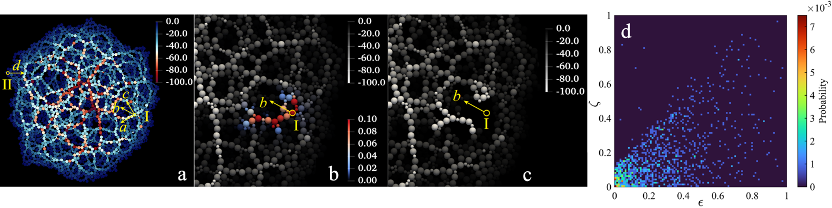
Figure 1. (a) Initial stress distribution of the bi-disperse aggregate. Particles are colored by the trace of stress tensor Tr(σ₀) and the negative sign means the compressed state. The redder the color, the larger the stress. Yellow circles and arrows denote the disturbed particles and directions of perturbation velocities respectively. (b) The particle speed (blue-red) at  τ=6.6×10^-4 superpose on the initial stress Tr(σ₀) in grey. Particles with u≤0.01 are invisible. (c) The post-impact particle stress trace Tr(σ). (d) The bi-variate probability scatter map in the ε-ζ plane at τ=6.6×10^-4.  ε=Tr(σ₀)-Tr(σ₀)_med and ζ=σ₁₂-σ_12med with (•)_med  denoting the median value. All the quantities are non-dimensional.

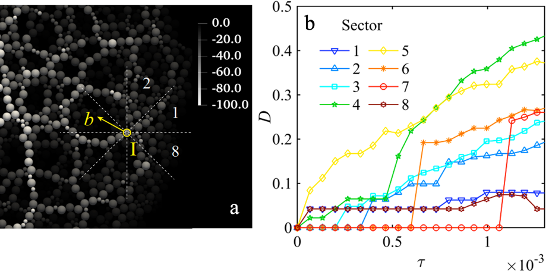
Figure 2. (a) A zoom on Tr(σ₀) around the location I, with the region divided into 8 sectors. (b) The evolution of D in the 8 sectors under impact perturbation b. All the quantities are presented in dimensionless form.

We also noticed that sliding and rolling failure events frequently occur in weak stress particles that are in contact with particles in the initial stress chains (Fig. 3a and 3b). When the magnitude of the perturbation velocity is large, the preference for response propagation remains unchanged, but particles near the disturbed particle exhibit significant displacement, and the particles scattered by the impact (coordinate number = 0) are predominantly distributed in the cavities formed by the initial stress chain structure (Fig. 3c).

Figure 3. Impact perturbation is applied on particle II along the direction d, as shown in Fig. 1a. (a) Particles that undergo sliding failure (yellow) superpose on the initial stress chains. u_impact=1.0, τ=6.6×10^-3. (b) Particles that undergo rolling failure (green). The same condition and moment as panel (a). (c) Particles with coordinate number = 0 (red). u_impact=100.0, τ=6.6×10^-3.

Impact perturbation simulations conducted in bi-disperse aggregates with surface boulders and power-law-distribution aggregates exhibit the same response propagation patterns. All the quantities are presented in dimensionless form.

Conclusion and Discussion: To conclude, the response to impact perturbations propagates preferentially along the initial stress chains, which bear the majority of the load induced by the residual impact kinetic energy. It suggests the impact disturbance may travel further than expected along these invisible paths, rather than dissipated uniformly in all directions from the impact crater. Particles in the weak stress regions enclosed by the initial stress chains are more easily scattered by impacts. Downstream of this work, we will focus on the extent and patterns of structural damage in the remaining rubble-pile asteroids and their dependency on impact perturbations.

Acknowledgments: C.H. is grateful for the hospitality of Imperial College London, where this work was carried out. C.H. is supported by the international joint doctoral education fund of Beihang University. Y.Y. acknowledges the financial support provided by the National Natural Science Foundation of China Grants No. 12272018.

Reference:

1. Ball, R. C. & Blumenfeld, R. Stress Field in Granular Systems: Loop Forces and Potential Formulation. Phys. Rev. Lett. 88, 115505 (2002).

2. Blumenfeld, R. Stresses in Isostatic Granular Systems and Emergence of Force Chains. Phys. Rev. Lett. 93, 108301 (2004).

3. Nicot, F., Hadda, N., Guessasma, M., Fortin, J. & Millet, O. On the definition of the stress tensor in granular media. Int. J. Solids Struct. 50, 2508–2517 (2013).

4. Cheng, B., Yu, Y. & Baoyin, H. Collision-based understanding of the force law in granular impact dynamics. Phys. Rev. E 98, 012901 (2018).

5. Cheng, B., Yu, Y. & Baoyin, H. Numerical simulations of the controlled motion of a hopping asteroid lander on the regolith surface. Mon. Not. R. Astron. Soc. 485, 3088–3096 (2019).

6. Cheng, B. et al. Reconstructing the formation history of top-shaped asteroids from the surface boulder distribution. Nat. Astron. 5, 134–138 (2021).