Modelling radar polarimetry of planetary surfaces

Introduction

Planetary surfaces are typically composed of particles from micrometer scale up to decimeter-to-meter scale. Particle morphology plays a key role in the polarimetric properties of planetary surfaces with wavelength-scale particles and thus, in understanding polarimetric observations of planetary bodies. Laboratory-characterised dust particles provide a pool of realistic compact particle shapes applicable for boulders as well; however, the morphological properties of the laboratory-characterised shapes can be challenging to parameterise analytically. Due to the sensitivity of the polarimetric properties on the shape of the scatterer,  the role of specific shape features in the polarimetric properties can be difficult to assess. Ensemble-averaged scattering properties are needed for modelling, but exact laboratory measurements are slow and challenging. Therefore, it is useful to find a geometrically parameterizable shape, which is also consistent with the scattering properties of the laboratory-characterised particles. Various studies have been published on the modelling of scattering properties of atmospheric mineral dust, planetary regolith, or coma particles with a number of methods for the generation of compact particles with more morphological complexity than spheroids: some examples include Gaussian particles [1,2], concave-hull transformations [2], Poisson-Voronoi tessellation [3], and various compact agglomerates [4]. Recent decades have also provided various opportunities for in-situ investigations of planetary regolith, and thus, for improved morphological characterisation of regolith, which can be useful for finding the key morphological parameters [e.g., 5,6].

In this work, we utilise polyhedrons with surface roughness and investigate their polarimetric properties as well as macroscopic interfaces with rough interfaces composed of sub-wavelength particles. The long-term goal is to understand the polarimetric observations of planetary bodies at optical wavelengths as well as the microwave domain. Due to the large parameter space in multiwavelength studies including diverse shapes, here we focus on radar polarimetry at and near the backscattering direction and a few selected particle properties. Radar observations provide disk-resolved images of planetary bodies illuminated by fully polarised incident waves, which enables intriguing scattering scenarios that are not typically observable in optical polarimetry.

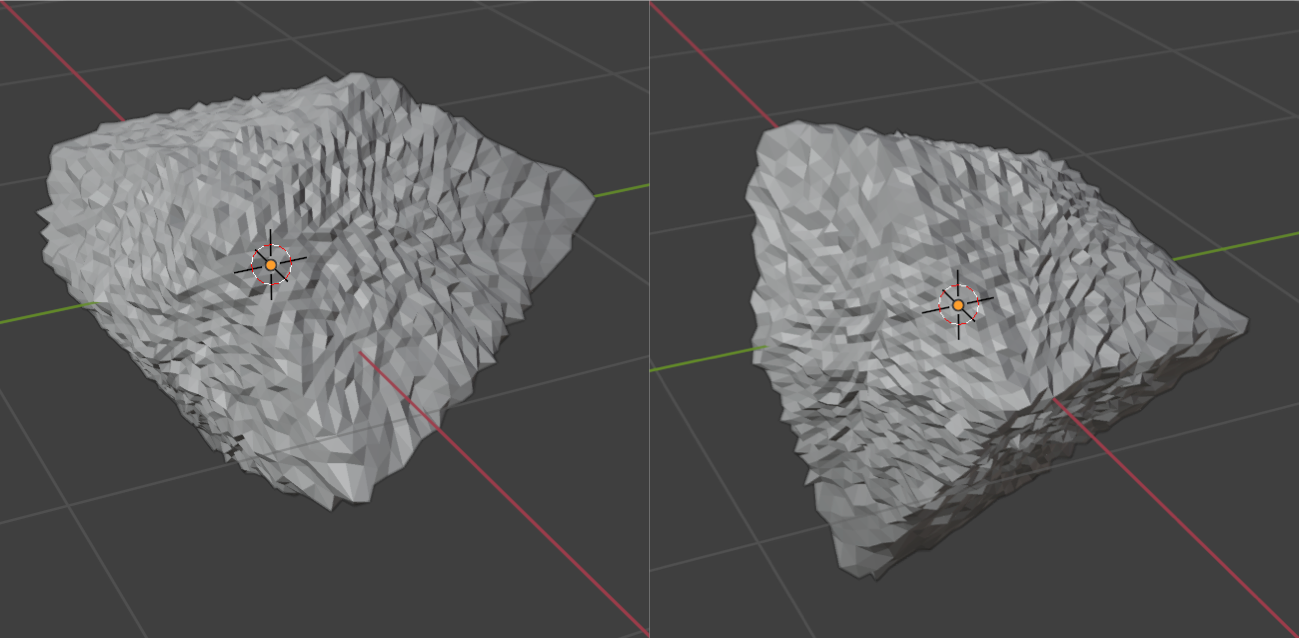
Figure 1. A polyhedral particle with 12 faces and a surface roughness standard deviation of 2% of the local vertex length, displayed in different orientations.

 

Particle morphology and numerical methods

The polyhedral particles with surface roughness are parameterised using any number of polygonal faces and small-scale surface roughness. The number of faces defines the sphericity statistically, as a sphere has essentially an infinite number of faces, whereas for example a hexahedron would have six faces. The particle is generated by Delaunay-triangularizing a unit sphere, then selecting a desired number of faces (here, 12-20) defined by randomly selected vertices (“seed vertices”), and scaling the length of the vertices based on their distance to the nearest seed vertex so that a flat face is formed. Finally, the surface roughness is applied using a Gaussian height distribution with a specified standard deviation. Figure 1 shows an example of one realisation of a rough polyhedral particle with 12 faces. We generated 20 realisations for each case to account for the stochasticity. The role of the particle sizes is investigated for size parameters (x=2πr_V/λ, where r_V is the radius of a volume-equivalent sphere and λ is the wavelength) from x=1 to at least x=10 or more depending on the refractive index; the computations are more time-intensive for greater refractive indices. In terms of the real part of the refractive indices, we considered values from 1.4 to 1.8 most relevant for the applications considered here, whereas for the imaginary part up to 0.01 was considered. The single-scattering properties were computed using the discrete-dipole approximation software ADDA [7].

Also polarimetric properties of rough interfaces are considered as in microwave applications the surface is composed primarily of densely-packed subwavelength-scale particles. For computations, we used an Improved Integral Equation Method Python code based on a Matlab code presented in [8].  

 

Preliminary results and discussion

We investigated the roles of particle size, shape, orientation, and material on the single-scattering properties. Also a variety of particle-size frequency distributions were applied as relevant for planetary remote-sensing applications. Due to the large parameter space, evaluating the role of specific particle properties on the polarimetric properties is challenging; however, we could observe that the size parameter, refractive index, and the shape and orientation play their own roles in an ambiguous way. The diagonal scattering matrix elements are extremely sensitive to the orientation, that is, the projected shape, but strongly correlate with each other for ensembles of particles at backscattering, as expected based on literature: P_1,1 – 2P_2,2 = P_4,4 [9], while P_2,2 = -P_3,3 [10], where P_i,j are scattering matrix elements at backscattering direction. 

The particle size is directly proportional to the polarisation ratios up to a certain size; however, the limiting size was found to vary based on other particle properties. The number of faces is a significant factor in determining how round the particles are statistically, and the roundness of the particles affects the amplitude of the fluctuations of the scattering matrix elements as a function of the scattering angle. For the case of 20 faces, two particles that were among the most elongated with a sharp edge on one side produced significantly different polarimetric properties more comparable to those produced by 12-face particles than the other 20-face particles. However, the role of the axis ratio was not self-evident, i.e., the axis ratio is only one factor among others. 

The presented scattering computations will be used for further computations to model scenarios where the individual particles form larger macroscopic structures and multiple scattering takes place.

References

[1] Muinonen et al. 1996, JQSRT 55(5):577; [2] Lindqvist et al. 2009, JQSRT 110:1398; [3] Ishimoto et al. 2010, JQSRT 111:2434; [4] Zubko et al. 2015, JQSRT 150:42; [5] Miyazaki et al. 2023, EPaS 75:171; [6] Wilkerson et al. 2024, Icarus 412, id. 115963; [7] Yurkin and Hoekstra, 2011, JQSRT 112:2234; [8] Ulaby and Long, 2014, Microwave Radar and Radiometric Remote Sensing, Artech House; [9] Mishchenko and Hovenier, 1996, Opt. Lett. 20:1356; [10] Van de Hulst, 1957, Light Scattering by Small Particles, Wiley.