Rapid technique for follow-up and precovery of asteroids

Introduction 

The knowledge of the current dynamic of Near Earth Asteroids (NEAs) is essential. Accurate astrometric measurements acquired over a large time span are important to provide reliable orbits and impact probability. With growing number of observations and a large number of already existing data, a rapid and accurate algorithm for follow-up and precovery of NEAs is required.

In this work we focus on precovery of asteroids. The New Astrometric Reduction of Old Observations (NAROO) program is dedicated to the measurement of astrophotographic plates and the analysis of old observations [1]. It has access to a collection of more than ten thousand plates from 1949 to 2000. Photographic plates consist of a substantial source of old observations of NEAs but they can be difficult to retrieve,  as positions predicted back in time from orbit propagation can be highly imprecise and the objects are generally faint.

Basic principles

The orbits of most of the NEAs, and in particular newly discovered ones, are not precise, therefore the accurate positions of these asteroids are unknown. In the majority of cases the trajectory itself is quite well defined, but there is an uncertainty in the position along the orbit. Over time, this uncertainty grows and can reach even the whole orbit (the mean anomaly is undefined). Because of that, our nominal prediction of the spherical coordinates of an asteroid on a photographic plate can be far from the real one. It is also possible that the nominal orbital solution tells us that the object is not on the plate, however, a significant part of the uncertainty region is, and, hence, there is still a probability that the object can be found on the plate.

Partial banana mapping method

In order to find if a Near-Earth Object can be on the photographic plate, we use a modification of a Partial Banana Mapping method [2]. In Fig. 1 one can see a schematic illustration of the method. The idea is that we take a covariance matrix of the asteroid in equinoctial orbital elements and consider the largest eigen vector of the matrix (which corresponds to the main axis of the curvilinear uncertainty region). Then we take several samples on this line (virtual asteroids) and project them onto celestial sphere with their uncertainties. This approach will give us the uncertainty region of the asteroid on the celestial sphere. If the region intersects with the plate, it means there is a chance of the object being on the plate and we can even provide the probability. We also estimate the length of the uncertainty region as well as visual magnitudes of the virtual asteroids.

Fig. 1. The scheme of the banana shaped uncertainty region of the asteroid. Point A is the nominal position of the asteroid. The bold line is the nominal asteroid’s orbit.

 

Computations

We tested the method with asteroid 2015 UM67 (506074) Svarog. In the test we simulated the scenario that it is the end of 2015 year, so we only have 3 months arc observations of the object. The result can be found in Fig. 2.

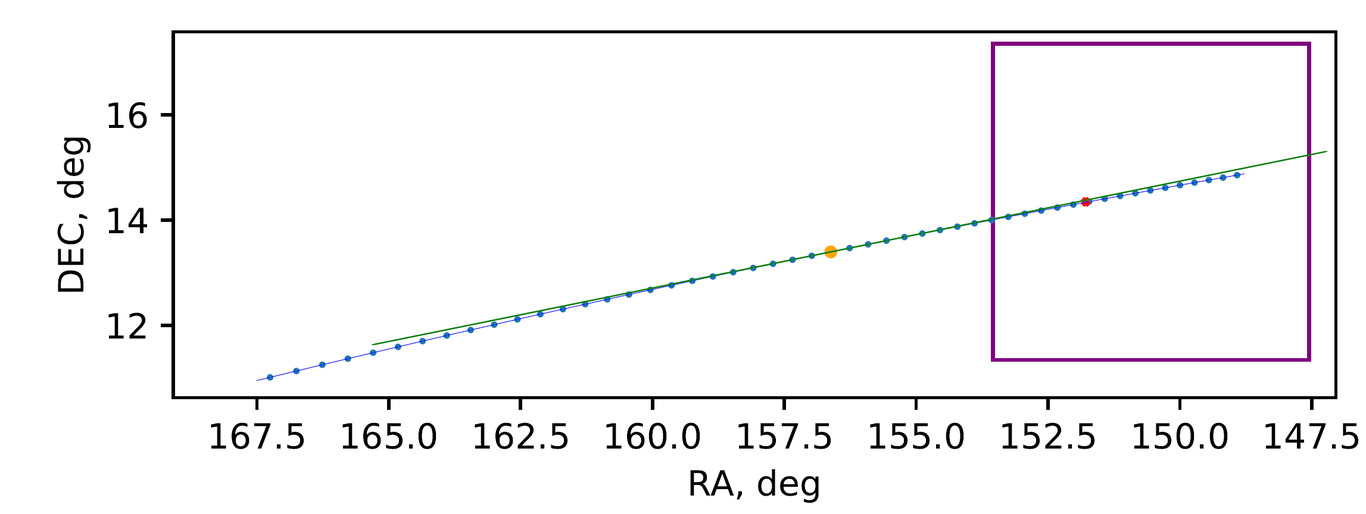
Fig. 2. Possible position (blue dots) of asteroid (506074) Svarog on 1990/03/01 06:00:00. The purple square represents the photographic plate. The orange dot is the nominal position of the object. The red dot in the plate is the position where the object was actually found. The green line is the uncertainty region of the nominal position constructed only from the covariance matrix in right ascension and declination.

 

As one can see the method could successfully predict the possible positions of the object and the actual observation is exactly in the 5 uncertainty region. This region is indeed curved, as one can compare it to the straight green line, directly obtained from the local covariance matrix. On the other hand, we can not get accurate predictions of the asteroid position using only the nominal position with its covariance matrix.

It took approximately 0.359 seconds to compute these results for asteroid Svarog on a PC with 12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz processor. On the contrary the Monte Carlo approach is required to integrate at least 1000 orbits of virtual asteroids and it takes 109.51 seconds (305 times longer!). This proves that our method is an efficient technique for asteroid follow-up and precovery.

To crossmatch all the NEAs with about 9000 photographic plates, available at Paris observatory, it takes only 1 day of computation.

Acknowledgments

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 101068341 “NEOForCE”. This study shows outcomes from the NAROO program which was supported by the DIM-ACAV of Ile-de-France region, PSL Research University, the Programme National GRAM and the Programme National de Planétologie (PNP) of CNRS/INSU with INP and IN2P3, co-funded by CNES.

References:

[1] Robert, V., Desmars, J., Lainey, V., et al. 2021, A&A, 652, A3.

[2] Vavilov D. E. (2020) MNRAS, 492, 4546–4552.