Revised analytic theory of the Yarkovsky force

1. Introduction

The Yarkovsky effect is a recoil force from the emitted thermal radiation that causes a slow change of asteroids’ orbits [1]. Its evolutionary significance includes spreading asteroid families and delivery of asteroids to the Kirkwood gaps thus re-supplying the population of near-Earth asteroids by the new members from the main belt, whereas its practical applications range from asteroid mass determination to prediction of asteroid hazard. Ordinarily the Yarkovsky effect is either estimated from an oversimplified linearized thermal model of a spherical asteroid or simulated fully numerically. The former path compromises the accuracy, whereas the latter conceals the physics. We choose the middle path between the spherical Scylla and the numerical Charybdis, and create a compromise theory that is simple for understanding and parametric analysis, sufficiently precise for practical use, and thoroughly verified at each step by comparison with numerical simulations.

2. Thermal model

For each surface element of the asteroid express the mean Yarkovsky force F_Y as

Here, A is the asteroid’s Bond albedo, L_Θ is the solar luminosity, S is the area of the surface element, r is the asteroid’s distance from the Sun, c is the speed of light, and p is what we call the dimensionless Yarkovsky pressure. This pressure is computed from the solution of the 1D heat equation under a surface element of a convex asteroid with zero obliquity. Under such assumptions, the solution of the non-dimensional heat equation depends on only two free parameters, namely the latitude ψ of the asteroid surface element and the thermal parameter θ, defined as in [2]. In addition to the commonly used analytic solution of the linearized heat equation valid for θ>>1, we also apply the approach of [3] to construct the opposite approximation θ<<1, and then proceed to the next iteration beyond the formalism of [3]. Then we sew together the two asymptotic solutions valid for the cases θ>>1 and θ<<1, thus obtaining a unified solution approximately valid for all θ:

Figure 1 illustrates this equation as a function of both θ and ψ, whereas Figure 2 compares different analytical and numerical calculations of p. 

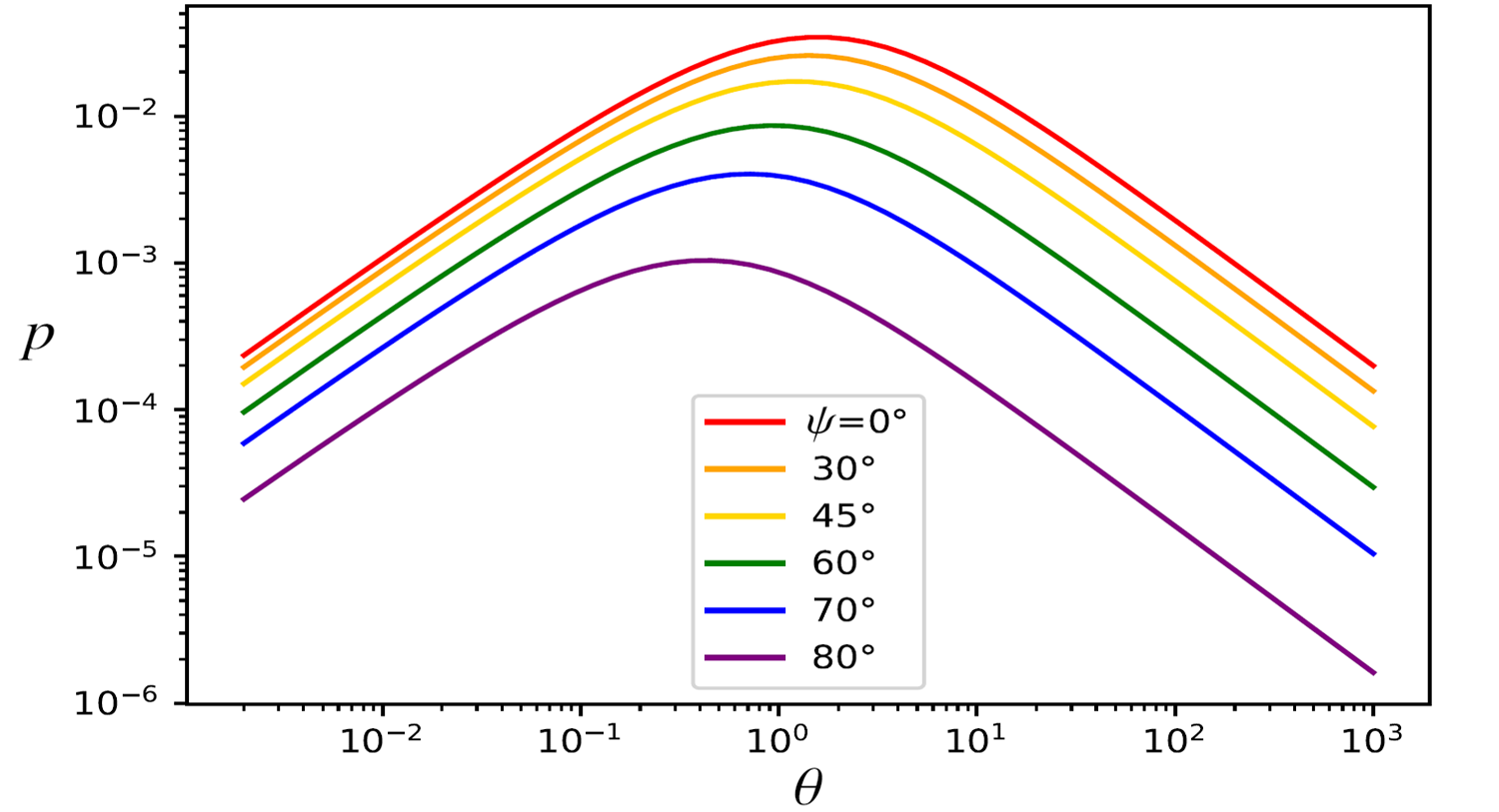
Figure 1. Dependence of the non-dimensional Yarkovsky pressure p on the thermal parameter θ and the latitude ψ. All the curves in the plot are self-similar.

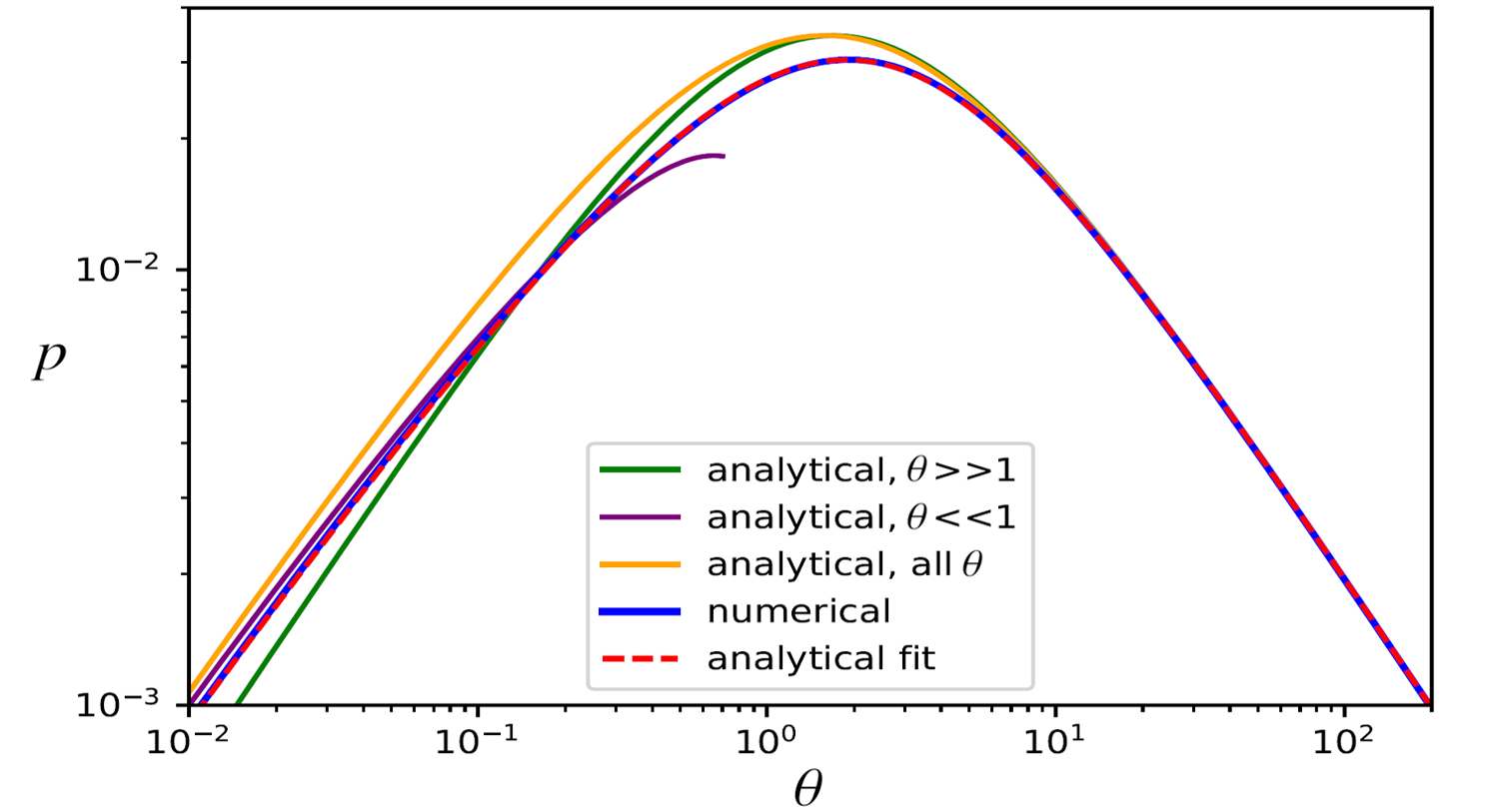
Figure 2. Comparison of p (ψ=0°) for the two analytic asymptotics, the sewed approximate solution, the numeric simulation, and an analytic fit.

The accuracy of the abovementioned analytic solution can be further improved by adding more free parameters to the expression and fitting them to the numerical solution, resulting in several different analytic fits with the accuracy ~1% each, that are virtually indistinguishable from the numerical simulation, one of them shown in Figure 2. In the left-hand side of Figure 2 we see that the linear thermal model (orange line) widely used for all θ [1] is wrong for θ<<1 (asymptotically by the factor of approximately 2).

3. Integration of the force over the asteroid’s surface

Next, several opportunities arize to integrate the Yarkovsky force over the asteroid surface: to integrate the approximate analytic expression for the force over a spherical or ellipsoidal asteroid, integrate it over a complex shape of a real asteroid, use the precise numerical expression for the Yarkovsky force… We explore all these possibilities, obtaining a set of expressions for the Yarkovsky effect of varying accuracy and complexity. One of such expressions is shown in Figure 3 in comparison with the Yarkovsky effect calculations for real asteroid shapes. It represents the factor f, by which the Yarkovsky effect of a spherical asteroid should be multiplied.

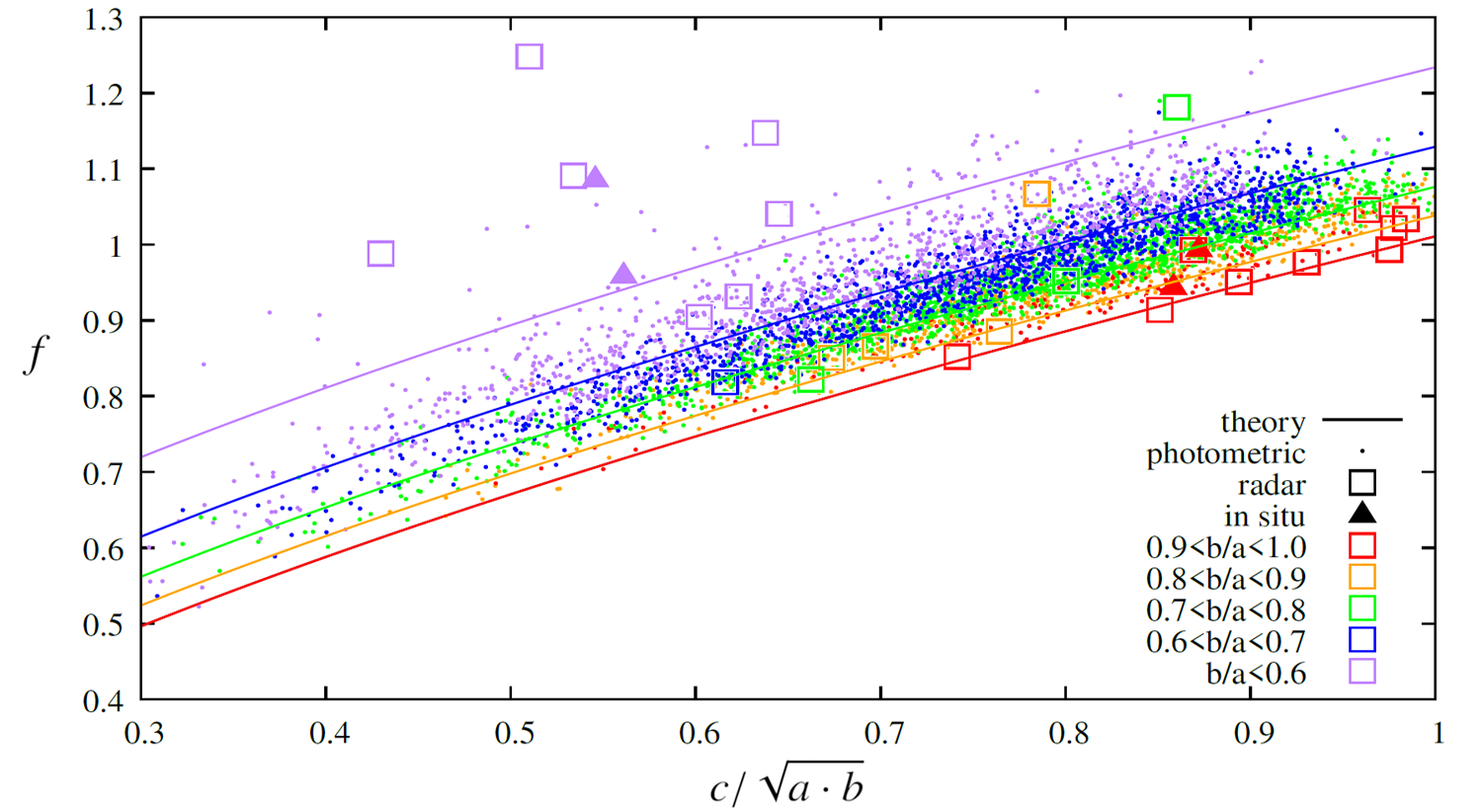
Figure 3. The shape factor  f  of the Yarkovsky effect plotted  as  a  function of asteroid  flattening  c/(ab)^1/2 and color-coded as a function of the asteroid’s equatorial axes ratio b/a. (With a, b, and c being the asteroid’s axes, longest to shortest.) Different shape datasets are represented with different types of symbols, and the theory for different axes ratios is shown with solid lines of corresponding colors.

4. Conclusion

As a part of a larger problem of improving the accuracy of the expression for the Yarkovsky drift rate, we revised the expression for the Yarkovsky pressure as a function of the thermal parameter and investigated the dependence of the Yarkovsky effect on the asteroid shape. The commonly used linearized thermal model of the Yarkovsky effect differs from our revised expression by the factor of approximately 2 for thermal parameters θ much less than or equivalent to 1, producing big errors in the Yarkovsky effect estimation for most of the studied asteroids. Fitting asteroids with 3-axial ellipsoids gives a good approximation to the Yarkovsky effect. These two corrections (on the thermal model and on the asteroid shape) dramatically increase the accuracy of the Yarkovsky effect prediction, but further refinements are needed to precisely account for the asteroid obliquity, orbit eccentricity, and the seasonal Yarkovsky effect.

Acknowledgements. This work was partially funded by the National Research Foundation of Ukraine, project N2020.02/0371 “Metallic asteroids: search for parent bodies of iron meteorites, sources of extraterrestrial resources”. OG is grateful to the European Federation of Academies of Sciences and Humanities (ALLEA EFDS-FL-16). VL acknowledges financial support from the German Excellence Strategy via the Heidelberg Cluster of Excellence (EXC 2181 - 390900948) “STRUCTURES”'. She also thanks for computing resources provided by the Ministry of Science, Research and the Arts (MWK) of the State of Baden-Württemberg through bwHPC and the German Science Foundation (DFG) through grants INST 35/1134-1 FUGG and 35/1597-1 FUGG, and also for data storage at SDS@hd funded through grants INST 35/1314-1 FUGG and INST 35/1503-1 FUGG.

References

[1] Vokrouhlický D. et al. (2015), in Asteroids IV (Tucson, AZ: Univ. Arizona Press), p.509-531; [2] Lagerros J. S. V. (1996), Astron. Astrophys., 310, p.1011-1020; [3] Golubov O. et al. (2016), Mon. Not. R. Astron. Soc., 458 (4), p.3977-3989.