Dynamical and photometrical model of Saturn’s A and B ring

Observational data have revealed an overwhelming amount of structure in Saturn's rings while indirectly inferring other structures. Most of the finest density variations are likely to have some internal origin. Two mechanisms have been proposed to explain the sub-kilometer scale structures observed in Saturn's inner-A and B rings: viscous overstability manifested as spontaneous growth of axisymmetric oscillations (Schmit & Tscharnuter, 1995) and self-gravity causing the emergence of transient tilted filamentary density-enhancements (Salo, 1992). Numerical experiments have indicated that both structures, overstable oscillations and self-gravity wakes, can coexist for certain ring physical and collisional properties (Salo et al., 2001). In particular, the importance of self-gravity relative to the disrupting tidal force of the planet, characterized by the r_h parameter, requires to be moderately weak for overstability to occur. However, the exact nature of the relationship between these two mechanisms is still poorly understood. Ballouz et al. (2017) have revealed that friction may mediate this interplay and, therefore, play a role in defining the final structure of the ring by allowing overstability to tolerate substantially stronger self-gravity, surviving in simulations with increased r_h.

As a first step towards a better understanding of the interplay between self-gravity and viscous overstability, we have investigated in a recent study the onset of viscous overstability in self-gravitating rings (Mondino-Llermanos & Salo, 2023, hereafter MS2023). The study involved performing an extensive survey of N-body simulations, covering a wide range of dynamical parameters. Dynamical simulations carried out using SoftIS code (Mondino-Llermanos & Salo, 2022) were restricted to the case of identical particles, leaving the cases of particle size distribution unexplored.

Salo et al. (2001) showed that overstability develops in simulations with a broad particle size distribution, albeit under more stringent conditions. Size distribution increases stability, presumably due to the increased velocity dispersion achieved by small particles. However, with an increase in dissipation, overstability is again achieved, even with size distribution. Therefore, we have extended our recent survey by performing particle size distributed simulations.

Figure 1: Examples of highly dissipative (ε=0.1) simulations with different particle size distribution widths. Left frame: Monte Carlo ray tracing image of a typical snapshot, seen from B=90° viewing direction and illuminated from B'=25°. Middle frame: Slice of the same snapshot through the equatorial plane. Label indicates the computed A₄₀ asymmetry amplitude (for definition see French et al., 2007). Right frame: Time-averaged surface density autocorrelation function. Label and red line indicate the effective wake pitch angle calculated from the longitude of minimum I/F brightness. Contour levels correspond to 10-50% overdensities.

 

We investigate the effect of size distribution on the viscous properties of the ring. The results support that measured total viscosity in Saturn's A-ring with a prominent wake structure should be a proxy for the contribution of gravitational torques. On the other hand, in agreement with results from MS2023, the presence of viscous overstability in the B-ring indicates that the non-local contribution is dominant in this region.

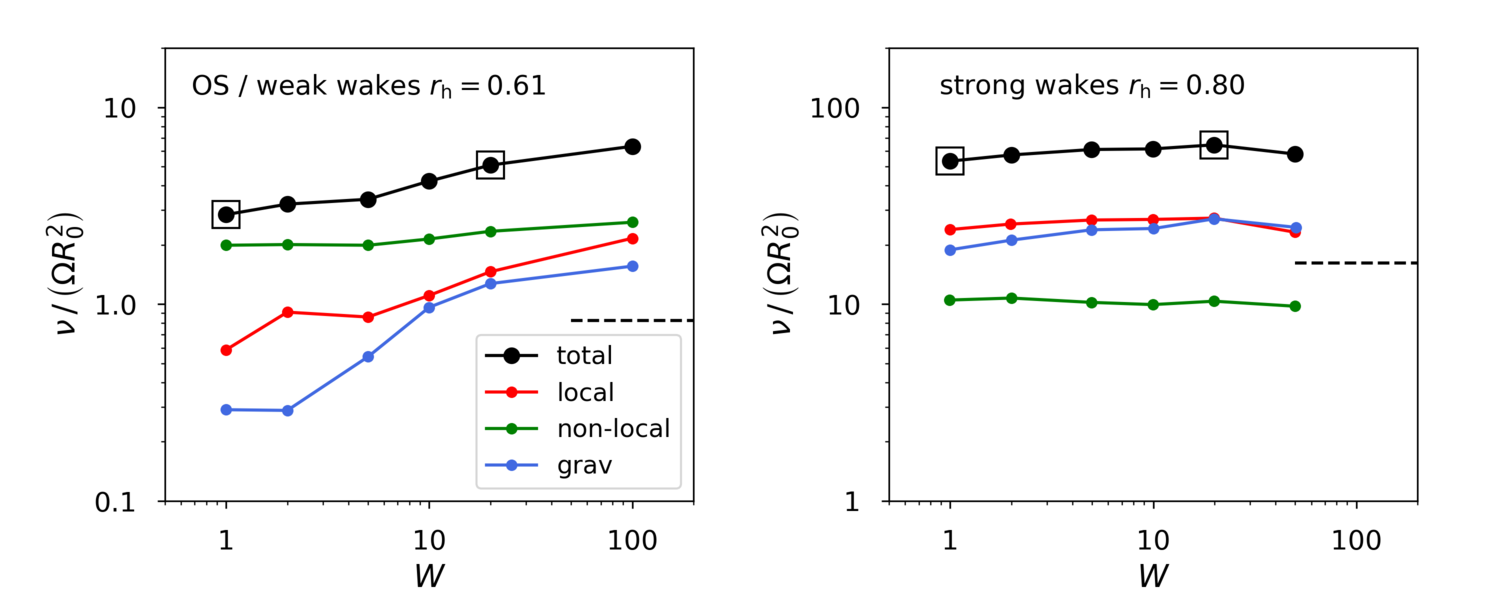
Figure 2: Comparison of the various contributions to total viscosity as a function of size distribution width for weak (left) and strong (right) self-gravity. The quantity R₀ in the normalization corresponds to the identical particle size that yields the same optical depth and surface density. Dashed lines indicate the gravity contribution estimated from Daisaka et al. (2001) viscosity formula. In all simulations, τ=1 and ε=0.1. Surface density is fixed in each frame.

 

We present the main consequences of incorporating this additional dimension in the parameter space together with a review of the factors determining the threshold density required for triggering viscous overstability and its subsequent suppression.

Figure 3: Examples of how size distribution affects the ring structure (simulations marked in Fig.2). 

 

Small-scale, systematically oriented density inhomogeneities covering a wide fraction of the ring area lead to a longitude-dependent brightness of the rings. The coexistence of overstable axisymmetric oscillations with inclined wake structures can lead to even more complicated photometric behavior as a function of illumination and viewing geometries.

We then present a detailed survey of the effects of the main dynamical parameters on the expected properties of self-gravitating planetary rings. Such an analysis employs our newly extended set of simulations in combination with the photometric simulation method in French et al. (2007). Figure 4 illustrates the consequences of self-gravity wakes and overstable oscillations on the ring brightness variations as a function of W, the width of the particle size distribution.

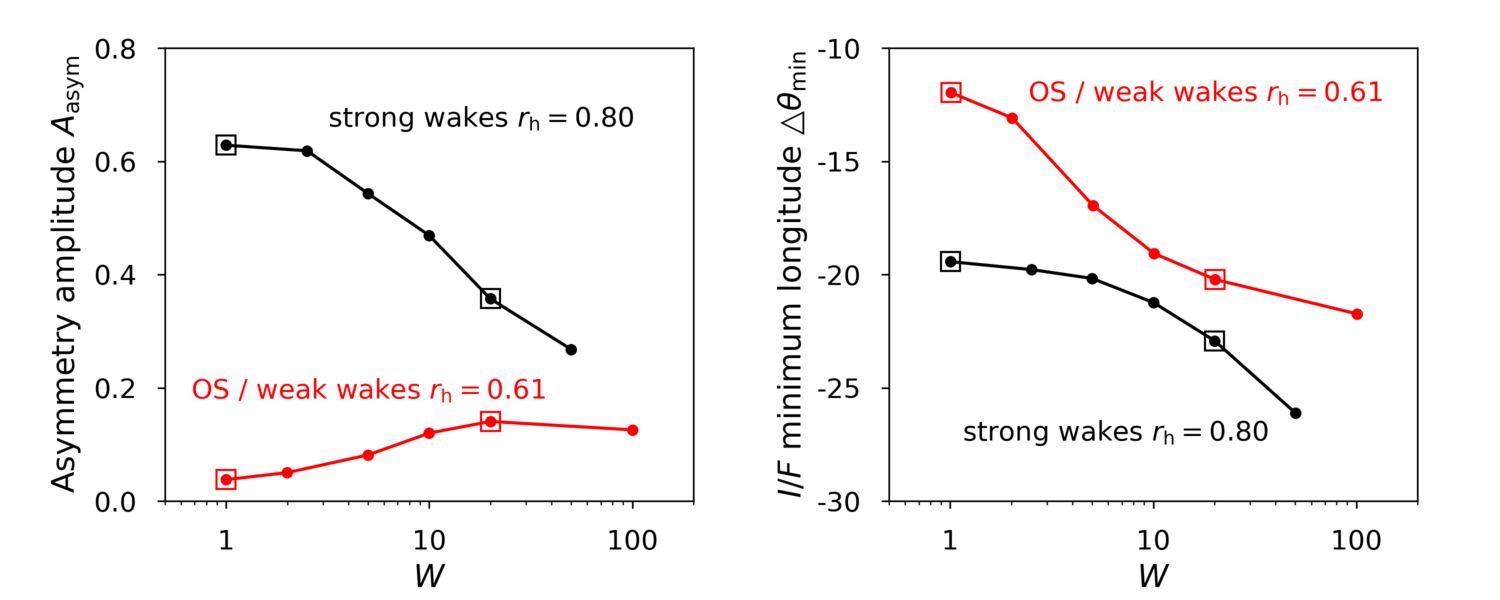
Figure 4: Effects of size distribution in the amplitude and longitude of minimum brightness with respect to ring ansa for simulations in Fig.2.

 

Our models emphasize the importance of size distribution in tandem with the strength of self-gravity. In a weak-gravity regime, increasing W can shift an overstable system to a wake-dominated system due to the increased strength of self-gravity resulting from increased filling factor inside the wakes (Fig.3). In the case of strong-gravity, size distribution reduces the asymmetry amplitude, although wakes remain dynamically strong (Figs. 2 and 4).

Finally, we apply the modeling tool to Saturn's rings to constrain the physical parameters of the ring particles based on the comparison with Hubble Space Telescope observations of the azimuthal asymmetry of the ring brightness. Constraints provided by opacity and viscosity measurements of B and A rings are also analyzed.

The models can match the constraints imposed by the azimuthal asymmetry and reproduce well the A and B ring opacity profiles. Moreover, the inclusion of size distribution significantly improves the match to observations. However, analysis of the HST asymmetry observations suggests very low internal densities ρ∼250kg/m3. Although this is a robust result, to be consistent with the measured A-ring viscosities, the possibility remains that particles are strongly affected by adhesion forces, in which case the particles could have significantly higher densities. This possibility is preliminarily addressed using hybrid models (see MS2023) that mimic these forces by leading to more vertically flattened self-gravitating wake structures.