Thermal stresses in small bodies approaching the Sun

Thermal stresses in small bodies approaching the Sun

Modern agglomeration models describe cometary nuclei as porous bodies with low
densities ( 0.1 g/cm³), yet observations of comets Halley and Shoemaker–Levy 9 indi-
cate significantly higher densities ( 0.6 g/cm³), suggesting a need to revise these models.
Thermal stress has emerged as a plausible mechanism for fragmentation, capable of op-
erating far from the Sun and without requiring tidal forces. Studies (Tauber and Kuhrt,
1987; Shestakova and Tambovtseva, 1997; Tambovtseva and Shestakova, 1999; ˇCapek
and Vokrouhlick´y, 2010) show that thermal stresses can exceed the tensile strength of
terrestrial materials.
This mechanism is also relevant to the origin of meteorites and near-Earth ob-
jects (NEOs). Research (Broˇz, M. et al., 2024) highlights the role of asteroid families
like Karin, Koronis, and Massalia in generating NEOs and ordinary chondrites. Car-
bonaceous chondrites are linked to bodies such as 3200 Phaethon, which may undergo
thermal disruption near the Sun.
We apply both analytical and numerical solutions of the heat diffusion equation
with one initial and two boundary conditions (Shestakova and Tambovtseva, 1997).
The analytical approach assumes constant thermal diffusivity and is restricted to ide-
alized parabolic orbits with zero perihelion, whereas the numerical model accounts
for temperature-dependent thermal diffusivity and realistic orbital configurations with
non-zero perihelion distance.
Spherical bodies made of crystalline ice, basalt, and chondrites are modeled along
parabolic orbits. Initial uniform temperatures are set at Tbb ≈ 150 K (3.45 AU) for
silicates and Tbb ≈ 30 K (86 AU) for ice, with final distances of 0.0345 AU (Tbb ≈
1500 K) and 4.95 AU (Tbb ≈ 125 K), respectively. Results show rapid internal heating
for small bodies, while larger ones retain cold interiors (see Fig. 1).
Comparison with strength lines (see Fig. 2) suggests that bodies with radii of 30 m
to 5 km may undergo fragmentation, even at distances from 10 AU to 40 AU.Smaller
fragments (with radii less than 30 meters) are unlikely to undergo thermal destruc-
tion, as they experience nearly uniform heating throughout their volume, resulting in
negligible internal temperature gradients and stress accumulation. Nevertheless, such
bodies are subject to active sublimation(Shestakova and Serebryanskiy, 2023) as they
approach the Sun. In contrast, larger nuclei (more than 1 km) retain a cooler interior and exhibit critical thermal stresses in the near-surface layers, which is consistent with the observed onset of coma formation during solar approach. The breakup of comet
Shoemaker–Levy 9 was likely initiated by this mechanism, with thermal fracturing
possibly preceding the tidal disruption (Shestakova et al., 2025).
According to Fig. 3, destructive internal stresses arise in basaltic, carbonaceous, and
ordinary chondritic bodies at heliocentric distances of approximately 2.5 AU, 2 AU,
and 1 AU, respectively. These stresses affect bodies with radii not exceeding 10 meters,
whose fragmentation is unlikely to produce observable dust clouds unless they pass
close to Earth such as ordinary chondrites with radii around 10 m. Near Earth’s
orbit, carbonaceous chondrites (40 m) and basaltic bodies (80 m) may also undergo
fragmentation ( ˇCapek and Vokrouhlick´y, 2010).Larger objects tend to break up closer
to the Sun, initiating a cascade of fragmentation. The resulting smaller fragments
continue to disintegrate, forming clouds of fine dust that may reach the sublimation
zone and become detectable via optical or infrared observations.

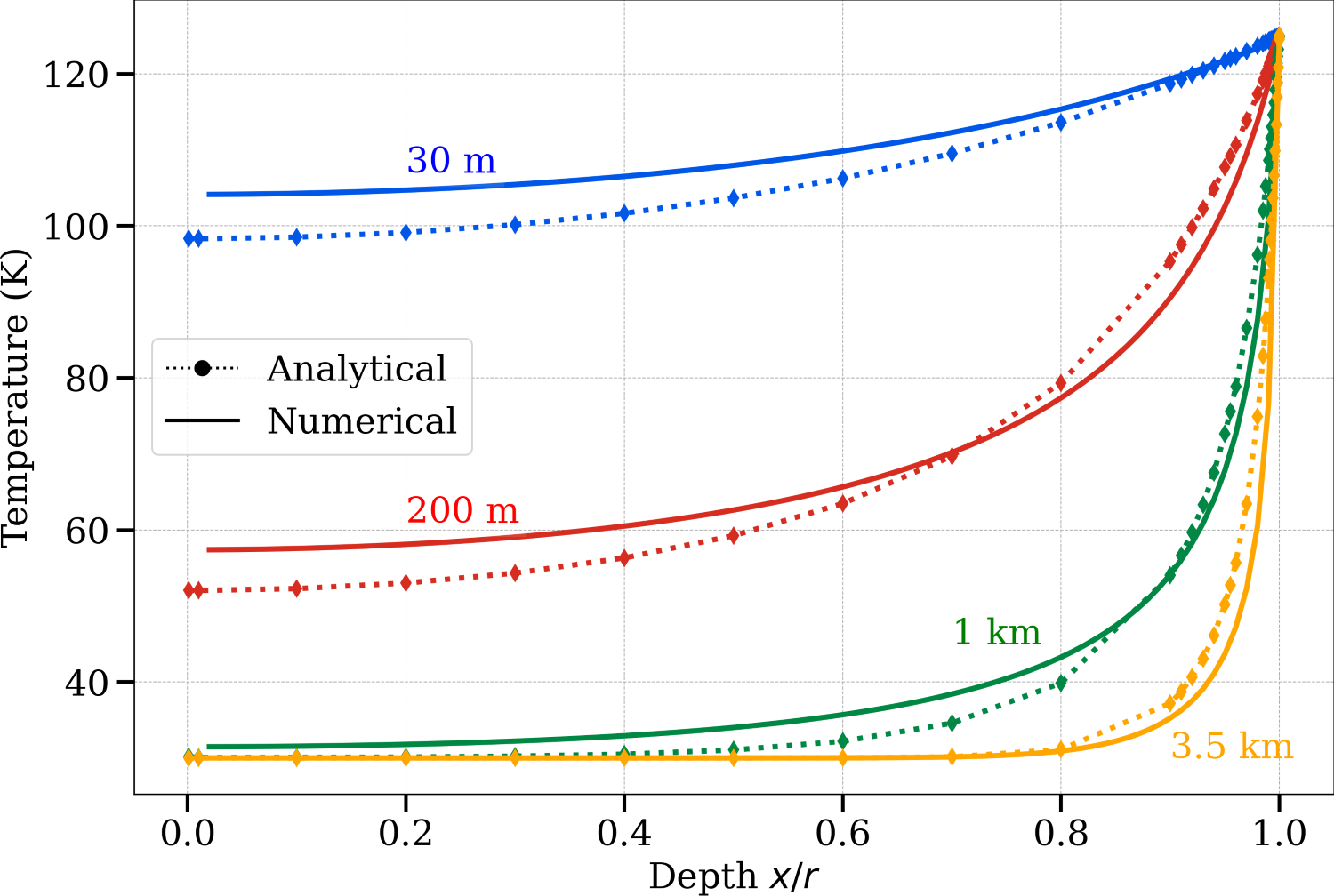
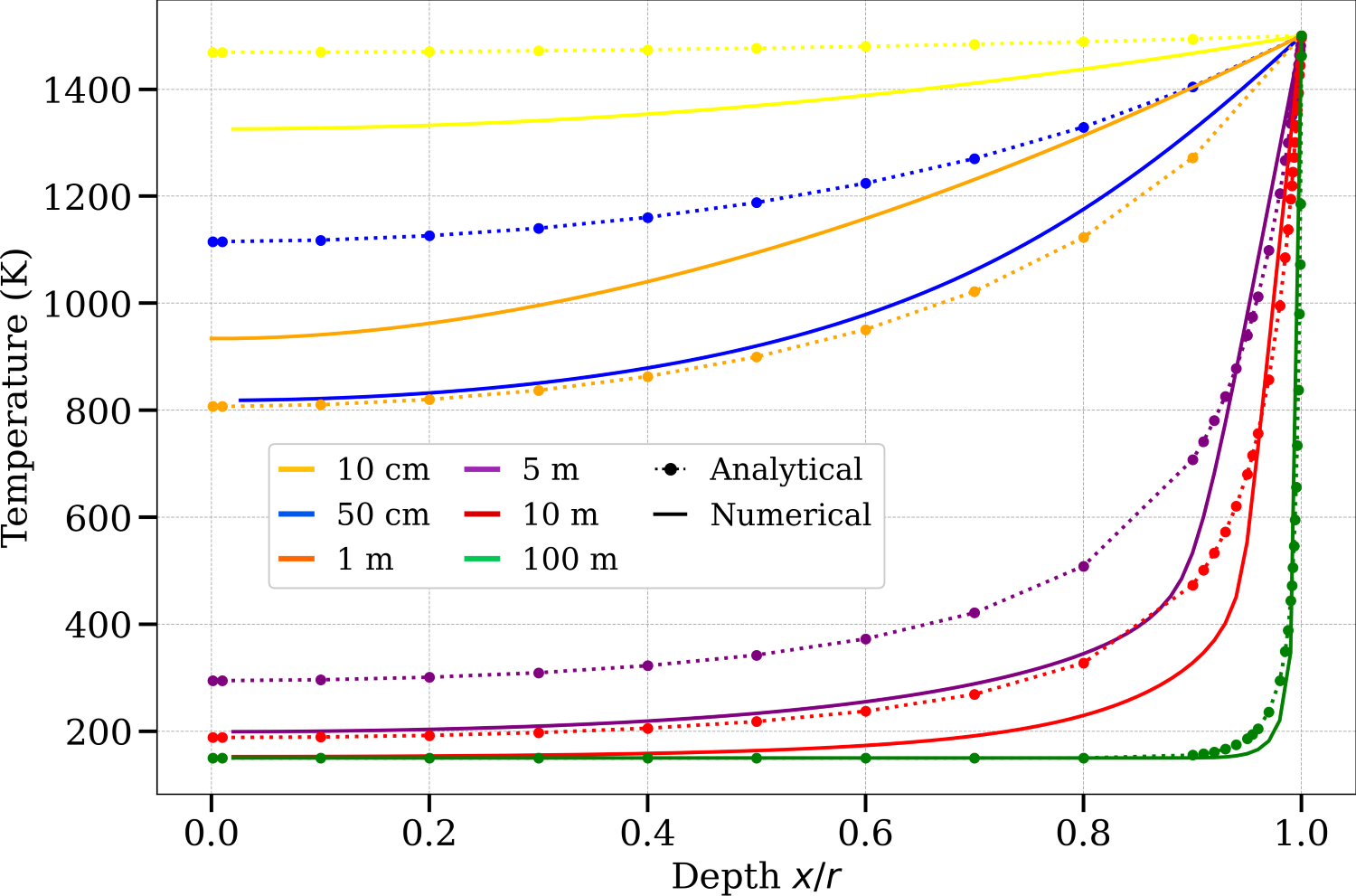
Figure 1: Temperature profiles from the center (x/r = 0) to the surface (x/r = 1) inside
bodies of various sizes at the final heliocentric distances of 0.0345 AU (7.42 R⊙) and 4.95 AU,
for chondritic material (left) and crystalline ice (right), respectively.

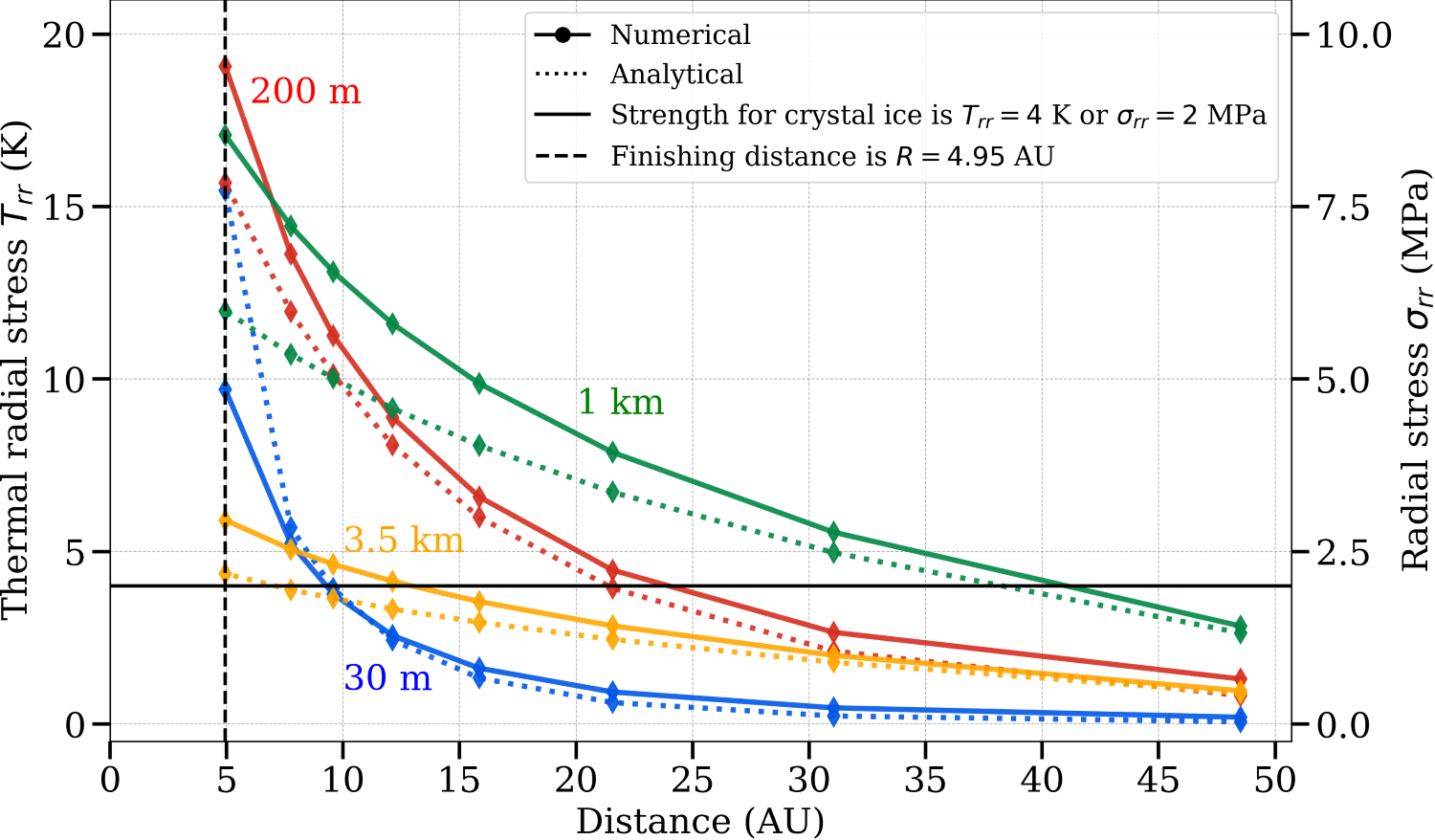
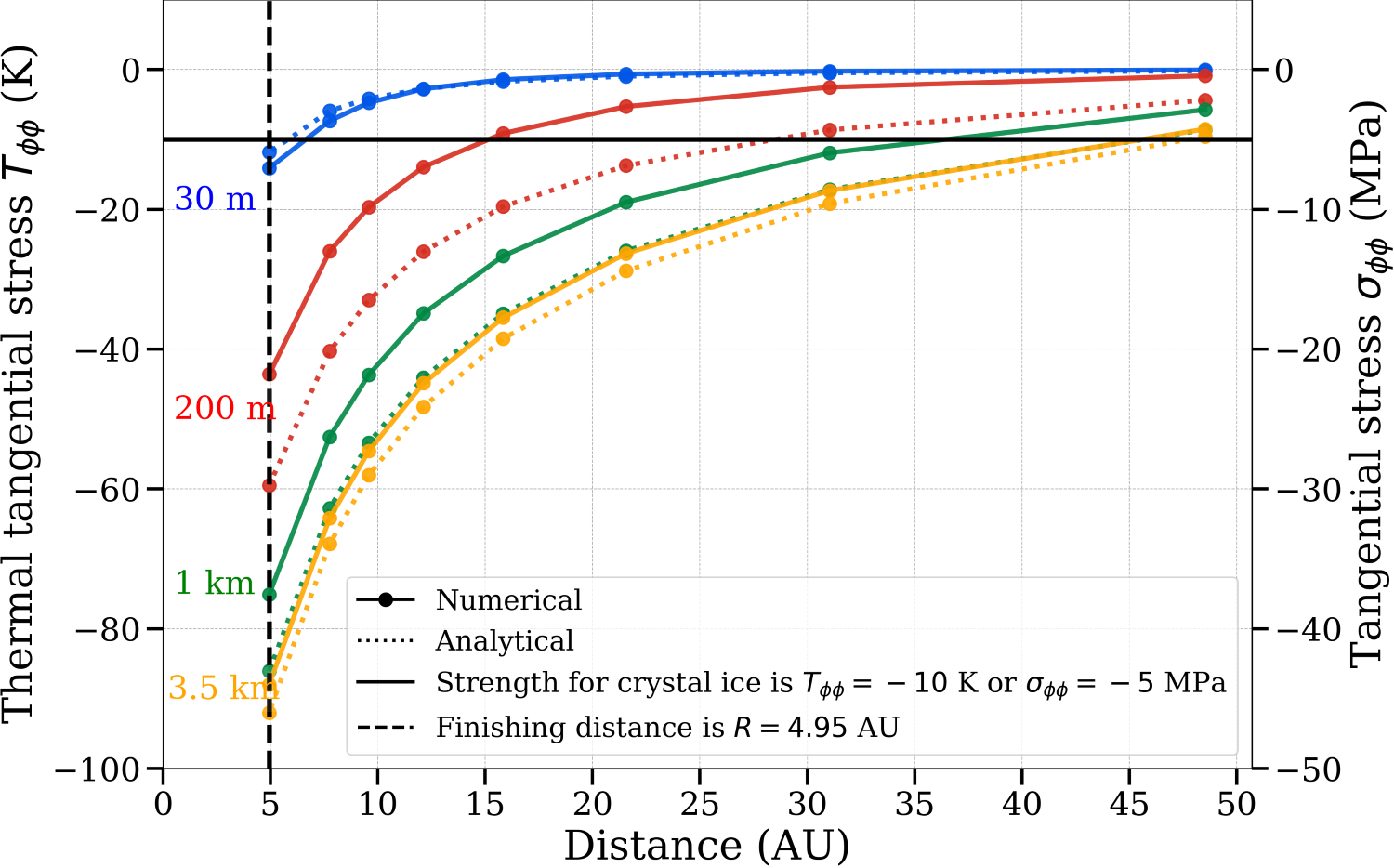
Figure 2: Thermal stresses at the center (x/r → 0, left) for the radial component and at the
surface (x/r = 1, right) for the tangential component, computed analytical and numerical at
various heliocentric distances from the initial position at 86 AU to the final point at 4.95 AU
for ice bodies.

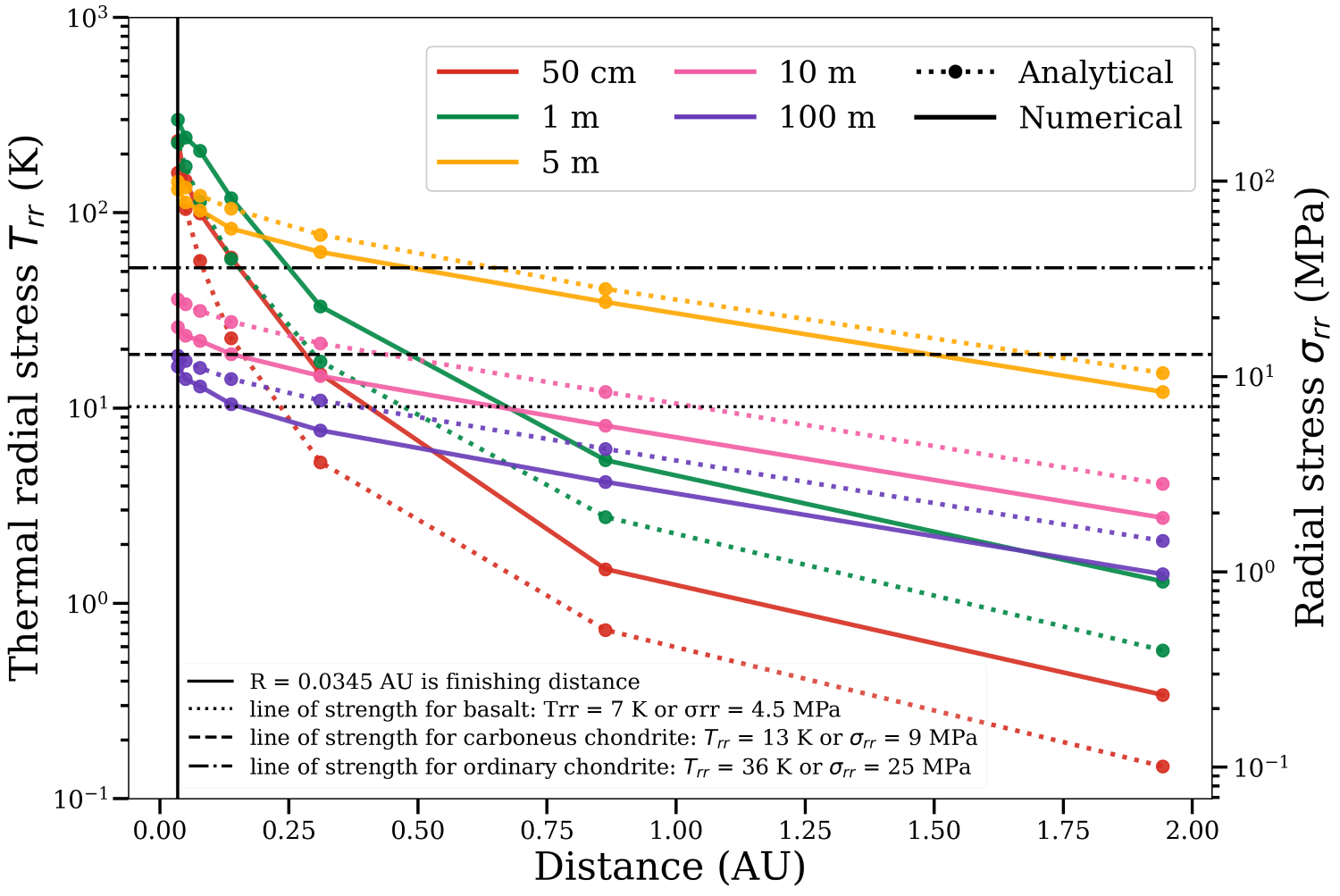
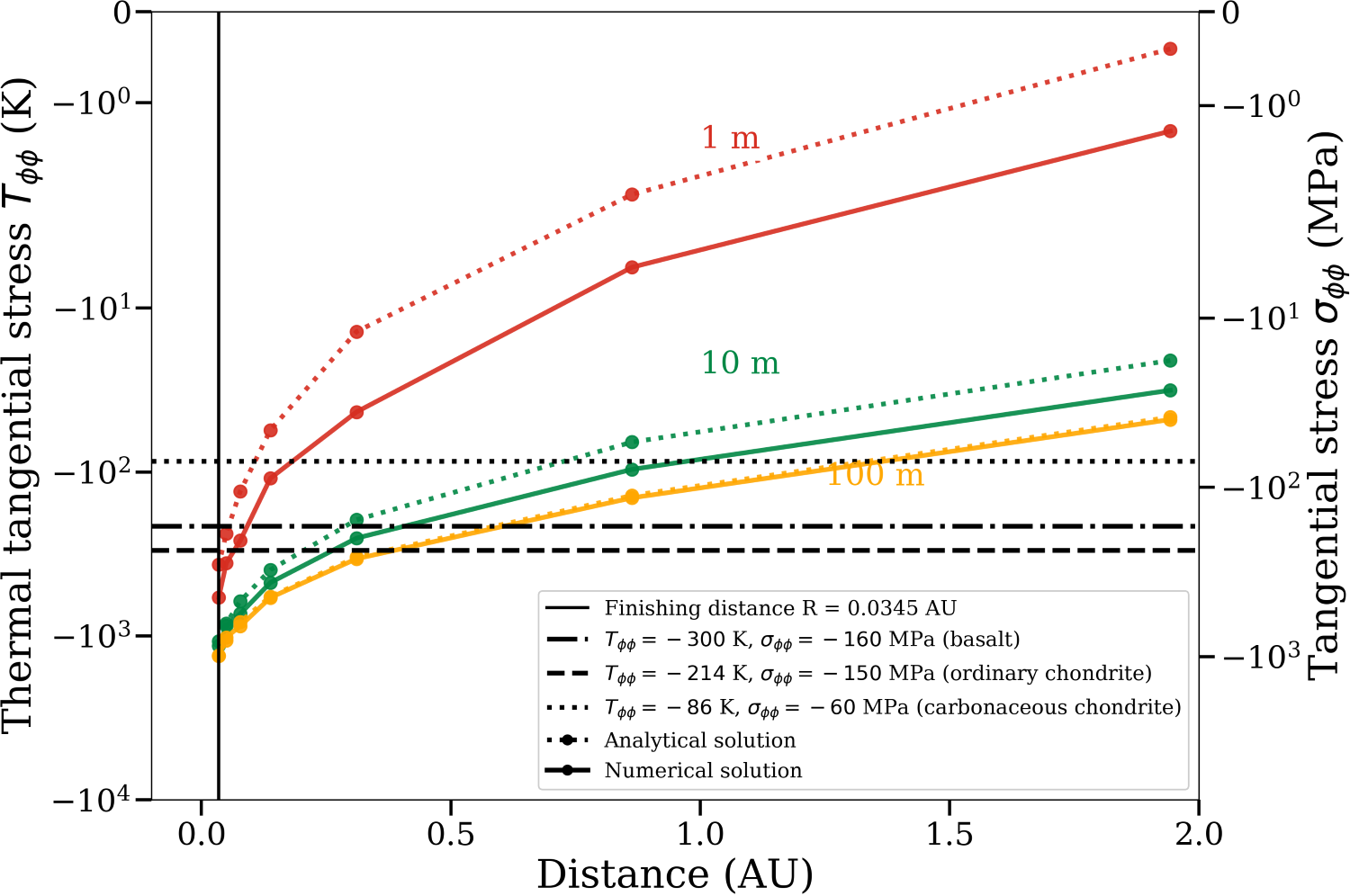
Figure 3: Thermal stresses at the center (x/r → 0, left) for the radial component and
at the surface (x/r = 1, right) for the tangential component, computed analytically and
numerically at various heliocentric distances from the initial position at 3.45 AU to the final
point at 0.0345 AU (≈ 7.42 R⊙) for chondritic and basalt bodies.

Acknowledgements: Our research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (programme no. BR20381077).

References
Broˇz, M., Vernazza, P., Marsset, M., Binzel, R. P., DeMeo, F., Birlan, M., Colas, F., Anghel,
S., Bouley, S., Blanpain, C., Gattacceca, J., Jeanne, S., Jorda, L., Lecubin, J., Malgoyre,
A., Steinhausser, A., Vaubaillon, J., and Zanda, B. (2024). Source regions of carbonaceous
meteorites and near-earth objects. AA, 689:A183.
Shestakova, L. I. and Serebryanskiy, A. V. (2023). On the new mechanism of planetary long-
period debris formation around white dwarfs. Monthly Notices of the Royal Astronomical
Society, 524(3):4506–4520

Shestakova, L. I., Spassyuk, R., and Omarov, C. (2025). Thermal stresses as a possible
mechanism for initiating the destruction of comet shoemaker–levy 9. Monthly Notices of
the Royal Astronomical Society, 537(2):2151–2159.
Shestakova, L. I. and Tambovtseva, L. V. (1997). The thermal destruction of solids near the
sun. Earth, Moon, and Planets, 76(1):19–45.
Tambovtseva, L. and Shestakova, L. (1999). Cometary splitting due to thermal stresses.
Planetary and Space Science, 47(3):319–326.
Tauber, F. and Kuhrt, E. (1987). Thermal stresses in cometary nuclei. Icarus, 69:83–90.
ˇCapek, D. and Vokrouhlick´y, D. (2010). Thermal stresses in meteoroids. i. implications for
small-scale splitting of meteoroids. Astronomy & Astrophysics, 519:A75.