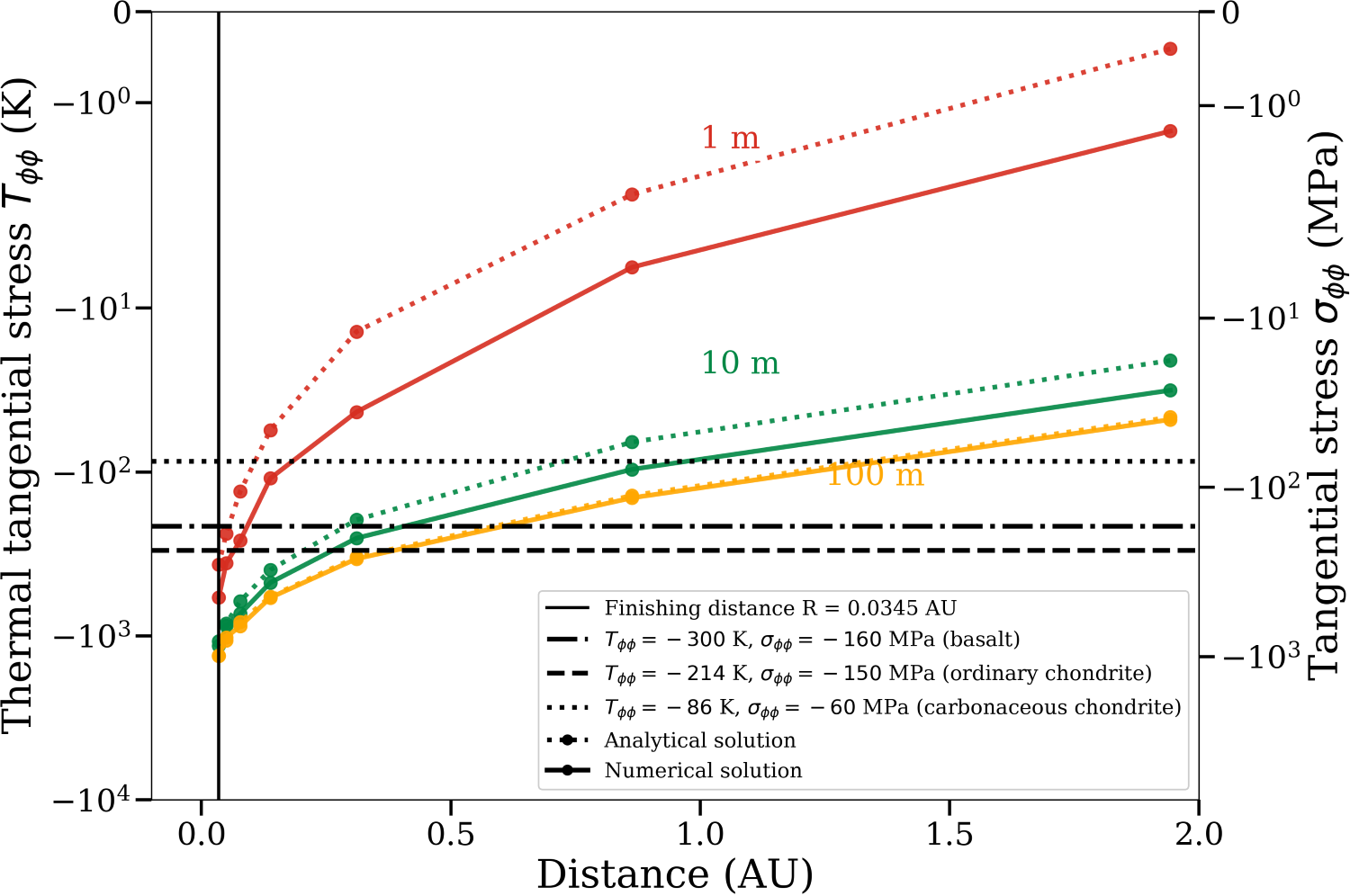
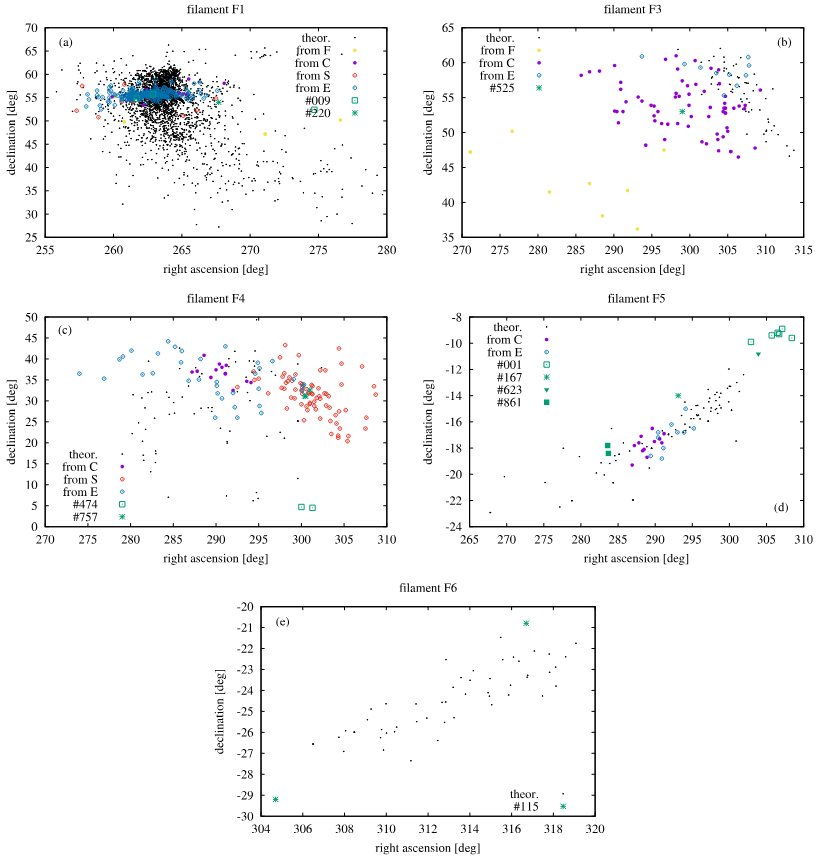
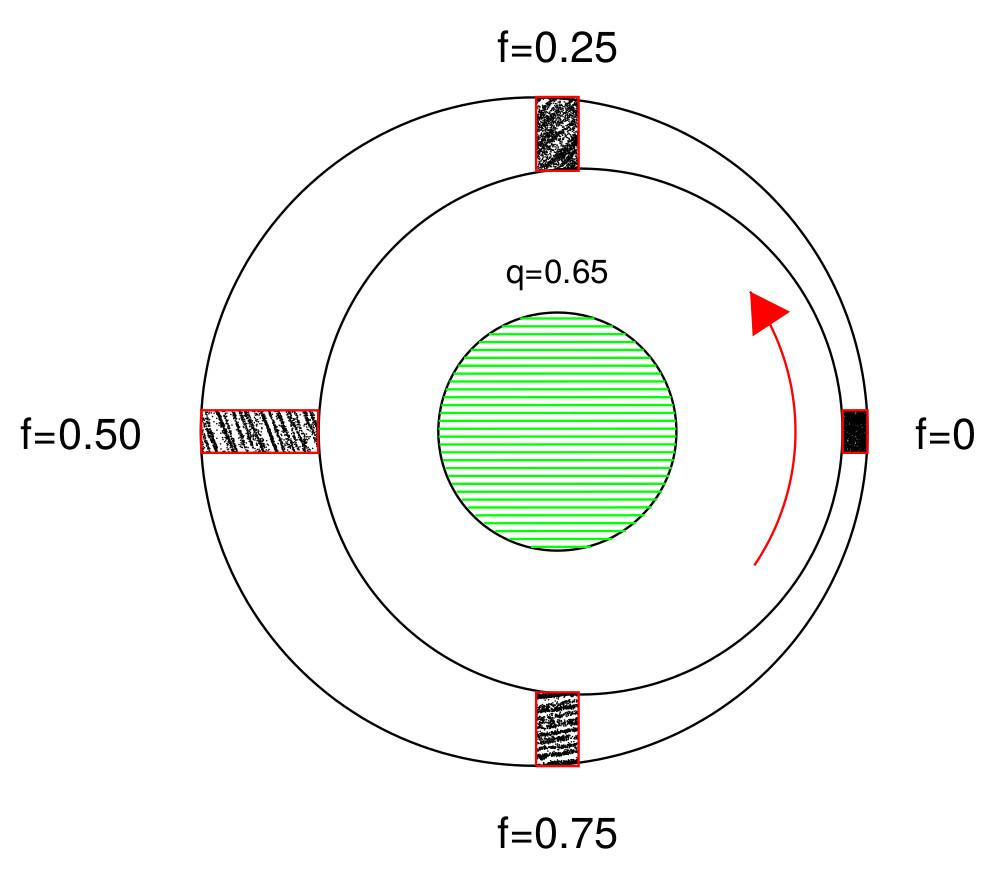
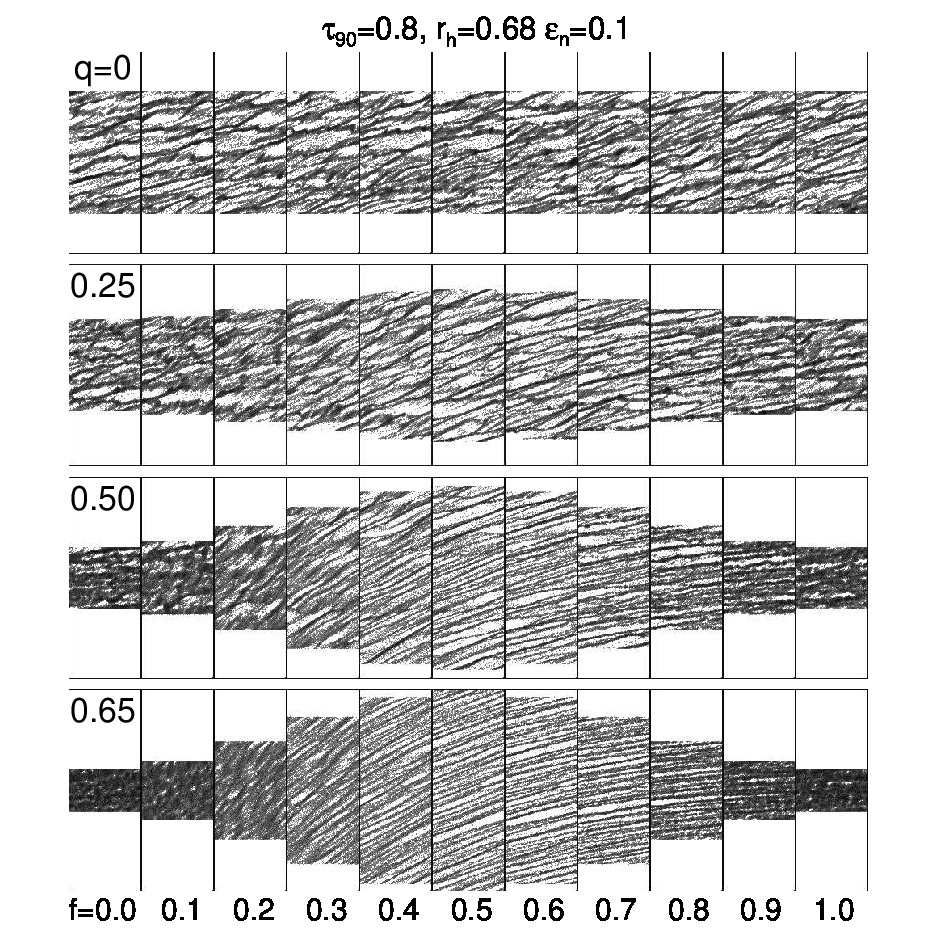
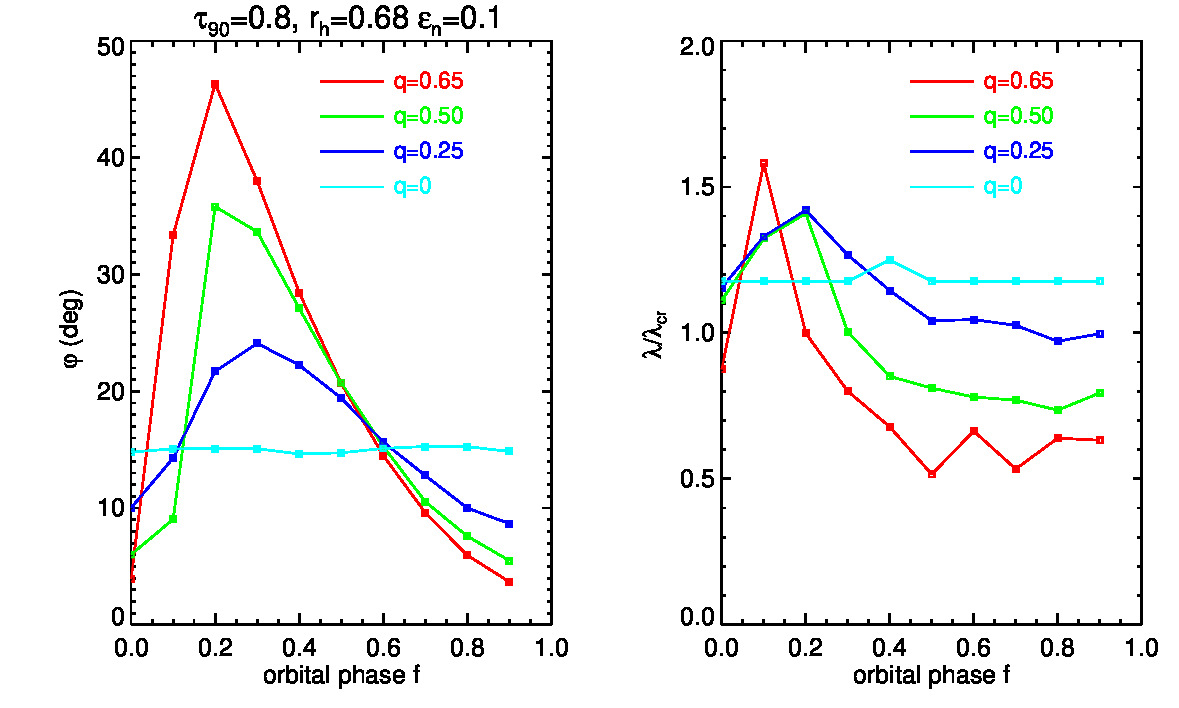
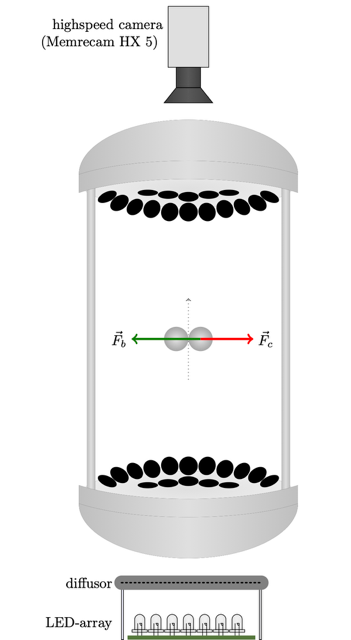
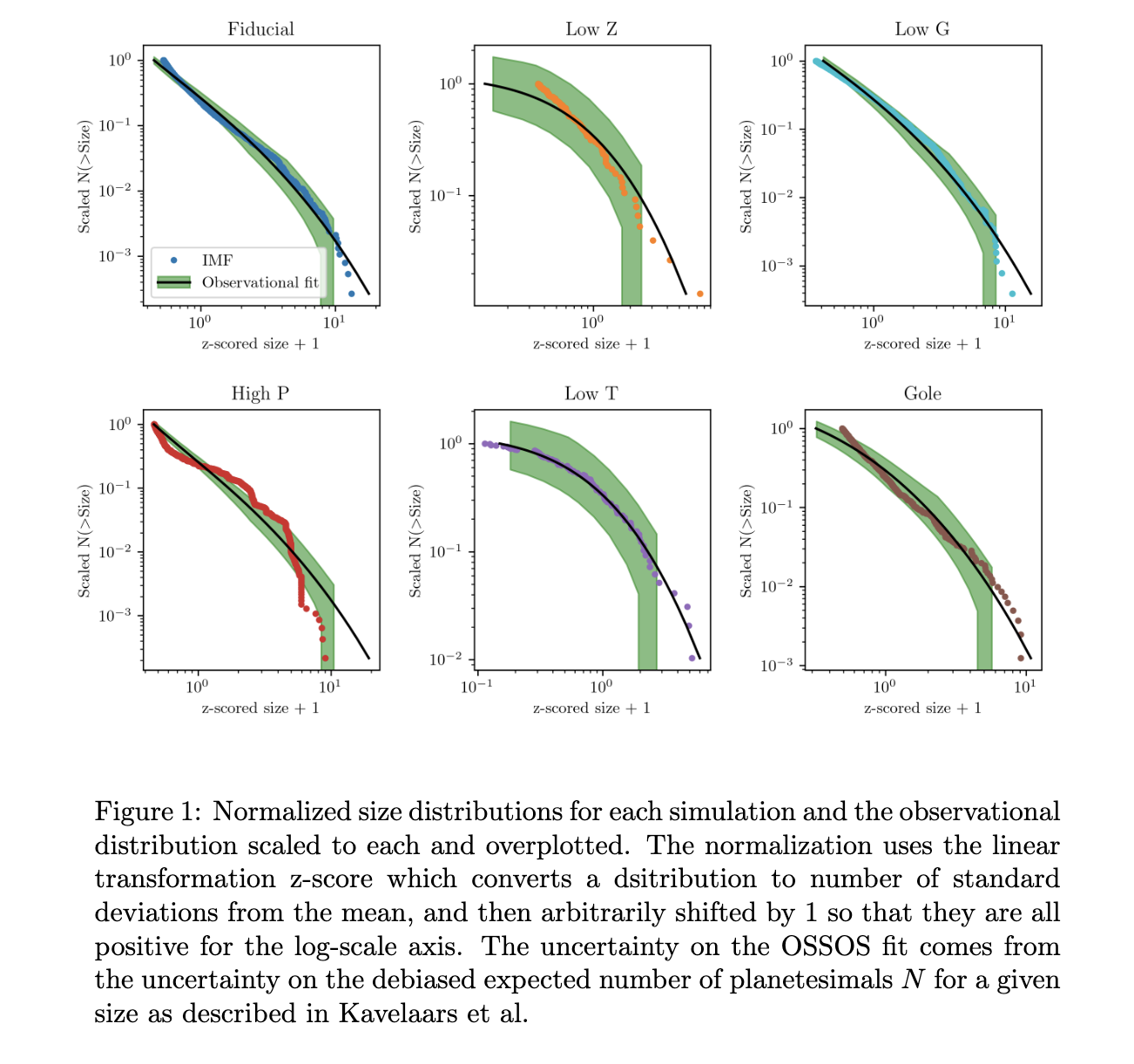
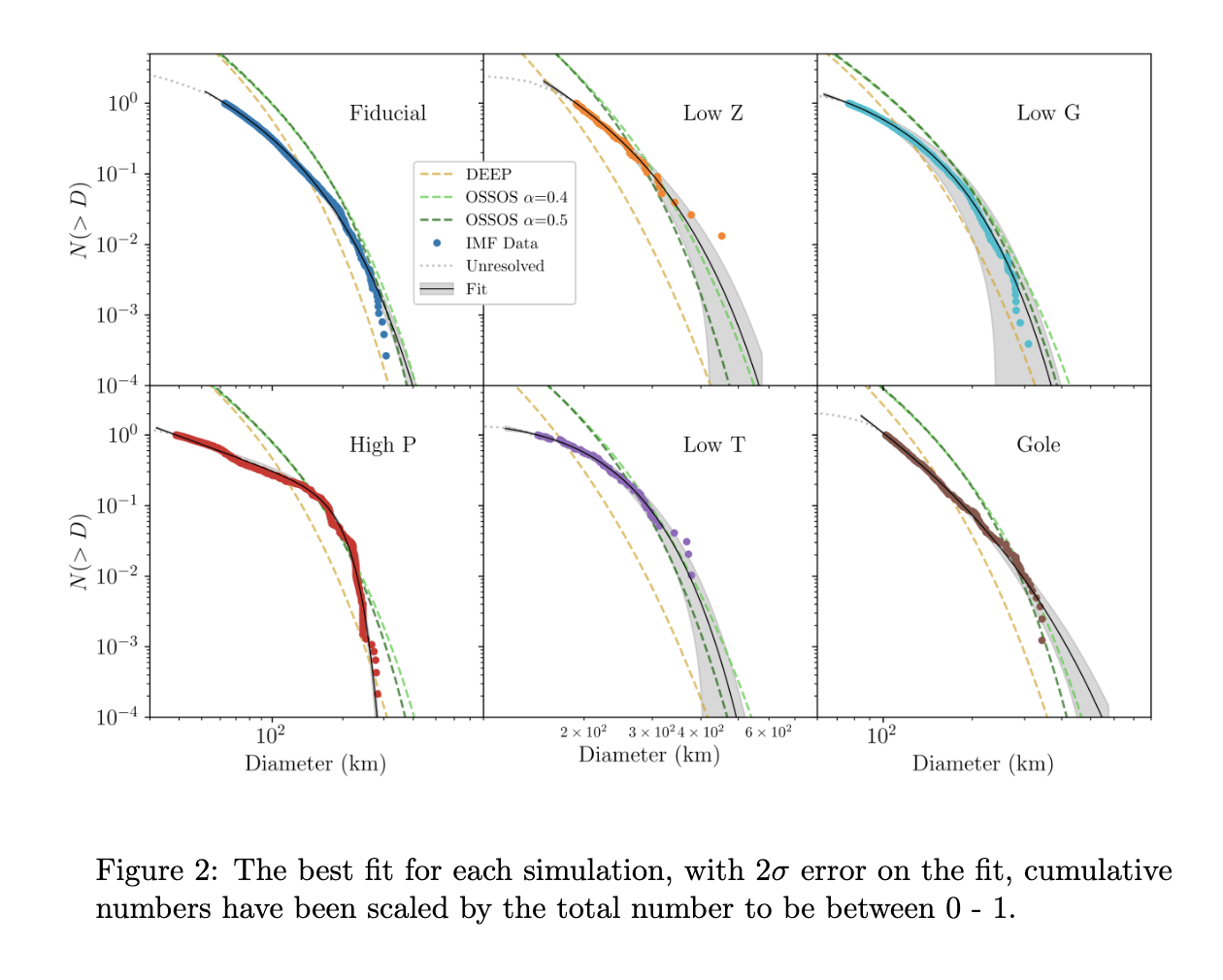
SB15
Computational and experimental astrophysics of small bodies and planets
Convener:
Vladimir Zakharov
|
Co-conveners:
Stavro Lambrov Ivanovski,
Ivano Bertini,
Raphael Marschall,
Nicholas Attree,
Nikolay Bykov
Orals MON-OB4
|
Mon, 08 Sep, 14:00–16:00 (EEST) Room Earth (Veranda 2)
Orals WED-OB6
|
Wed, 10 Sep, 16:30–18:30 (EEST) Room Mercury (Veranda 4)
Posters MON-POS
|
Attendance Mon, 08 Sep, 18:00–19:30 (EEST) | Display Mon, 08 Sep, 08:30–19:30 Finlandia Hall foyer, F170–186
This session will include an introduction and discussion of new and/or existing laboratory studies in simulated space-like environments and models, experimental techniques, computational methods that can address the results of analytical, experimental and numerical analysis (with respect to computational methods and algorithms of solution) on the above described studies.
Abstracts on thermophysical evolution models of small bodies interiors as well as on the modeling of atmosphere and exosphere are welcome.
Session assets
Comets&Asteroids
14:00–14:12
|
EPSC-DPS2025-195
|
On-site presentation
14:12–14:24
|
EPSC-DPS2025-522
|
ECP
|
On-site presentation
14:24–14:36
|
EPSC-DPS2025-466
|
ECP
|
On-site presentation
14:36–14:48
|
EPSC-DPS2025-19
|
On-site presentation
14:48–15:00
|
EPSC-DPS2025-868
|
ECP
|
On-site presentation
15:00–15:12
|
EPSC-DPS2025-825
|
On-site presentation
15:12–15:24
|
EPSC-DPS2025-1940
|
On-site presentation
15:24–15:36
|
EPSC-DPS2025-1599
|
ECP
|
On-site presentation
15:36–15:48
|
EPSC-DPS2025-790
|
ECP
|
On-site presentation
15:48–16:00
|
EPSC-DPS2025-1560
|
ECP
|
On-site presentation
Planetesimals, Small Bodies & Rings
16:30–16:42
|
EPSC-DPS2025-11
|
On-site presentation
16:42–16:54
|
EPSC-DPS2025-111
|
On-site presentation
16:54–17:06
|
EPSC-DPS2025-1426
|
ECP
|
On-site presentation
17:06–17:18
|
EPSC-DPS2025-282
|
ECP
|
On-site presentation
17:18–17:30
|
EPSC-DPS2025-355
|
ECP
|
On-site presentation
17:30–17:42
|
EPSC-DPS2025-247
|
ECP
|
On-site presentation
17:42–17:54
|
EPSC-DPS2025-519
|
ECP
|
On-site presentation
17:54–18:06
|
EPSC-DPS2025-497
|
On-site presentation
18:06–18:18
|
EPSC-DPS2025-130
|
On-site presentation
18:18–18:30
|
EPSC-DPS2025-929
|
ECP
|
On-site presentation
Dust, Planetesimals, Comets, Asteroids, Rings
F170
|
EPSC-DPS2025-1103
|
ECP
|
Virtual presentation
F171
|
EPSC-DPS2025-332
|
ECP
|
On-site presentation
F172
|
EPSC-DPS2025-457
|
On-site presentation
F176
|
EPSC-DPS2025-1832
|
On-site presentation
F177
|
EPSC-DPS2025-1493
|
ECP
|
On-site presentation
F178
|
EPSC-DPS2025-391
|
On-site presentation
F179
|
EPSC-DPS2025-1335
|
ECP
|
On-site presentation
F180
|
EPSC-DPS2025-726
|
ECP
|
On-site presentation
F181
|
EPSC-DPS2025-1812
|
On-site presentation
F182
|
EPSC-DPS2025-321
|
On-site presentation
F183
|
EPSC-DPS2025-1440
|
ECP
|
On-site presentation
F184
|
EPSC-DPS2025-783
|
On-site presentation
F185
|
EPSC-DPS2025-1558
|
ECP
|
On-site presentation
F186
|
EPSC-DPS2025-559
|
ECP
|
Virtual presentation
Investigating dynamically linked near-Earth asteroids: Orbital evolution and possible separation mechanisms
(withdrawn)