Resonant Dynamics and Particle Trapping Around Non-Symmetric Asteroids

Asteroids exhibit intricate dynamical environments due to their irregular, nonspherical shapes, which give rise to complex gravitational fields capable of inducing chaotic motion in surrounding particles. Despite this apparent disorder, regions of periodic and resonant motion can emerge. These periodic and resonant structures, shaped by the gravitational asymmetry of the central body, are particularly evident in the body-fixed reference frame. In particular, resonant dynamics can provide valuable insight into the long-term evolution of ejecta, dust particles, and debris, as it can lead to their temporary or permanent trapping around small bodies. These mechanisms can drive the redistribution of material, with implications for regolith transport, debris retention, and the transition from transient to bound orbits [1]. In recent years, these dynamics have gained growing interest, especially for their relevance to early satellite formation, binary asteroid development, and the formation of rings or secondary bodies. Examples such as the rings observed around Chariklo and Haumea, suggesting  that these irregular bodies can host coherent structures maintained by resonant mechanisms [2].

Several studies have explored the influence of non-spherical gravitational potentials on resonant dynamics near small bodies [2][3], often relying on simplified representations such as ellipsoids, localized mass anomalies, or low-degree spherical harmonic models.

In this work, we model the deviation from spherical symmetry using a higher-order spherical harmonics expansion up to degree and order six, which proves sufficient to resolve resonant features close to the body. The approach is applied to the primary of the Didymos system, the binary asteroid targeted by ESA’s Hera mission, whose binary nature makes it an ideal case for investigating capture processes and the potential formation of secondary bodies.

An object is said to be in a p₁ : p₂ gravitational resonance when its orbital period and the rotational period of the central body satisfy the commensurability condition p₁Ω = p₂ n, where n denotes the mean motion of the particle (related to its orbital period in the inertial frame), and Ω is the rotational rate of the central body.

Near irregularly shaped bodies, it is more effective to adopt a body-fixed, co-rotating frame, in which the gravitational potential becomes time-invariant, and so problem autonomous, making it suitable for identifying resonance islands and stable regions through techniques such as Poincaré surface of section analysis. To provide a more intuitive and geometrically meaningful interpretation of resonances in the body-fixed frame, an alternative definition can be employed [6]. By defining the radial (epicyclic) frequency κ, which describes how frequently the particle returns to periapsis, and the synodic frequency, n−Ω, which indicates how often the particle returns to the same spatial location in the co-rotating frame, the resonance condition can be reformulated as: κ = k( n−Ω), which corresponds to a k : (k − j) resonance: n/Ω∼k/(k-j).

Here, j represents the number of distinct types of sectors traced by the resonant orbit, while k indicates the number of identical sectors. Moreover, j also corresponds to the number of intersections on the Poincaré surface of section, offering a direct link between orbital resonances and visual structures in phase-space.

The phase-space structure around Didymos has been initially explored through Poincaré sections, revealing the emergence of resonant features and periodic orbit islands.  The resonances identified through these maps are then examined in using a Hamiltonian formalism. Through this approach, it becomes possible to construct portraits of the resonant phase-space, providing insights into the location of equilibrium points, the amplitude of libration and circulation zones, and the overall stability and dynamical features associated with a specific resonance.

This analysis is complemented through the use of a dynamical indicator: the Finite-Time Lyapunov Exponent (FTLE). This chaos indicator highlights the sensitivity of trajectories to initial conditions and is effective in capturing a broader picture of the system’s behavior. FTLE maps offer a useful benchmark for comparing results obtained via the classical Hamiltonian framework.

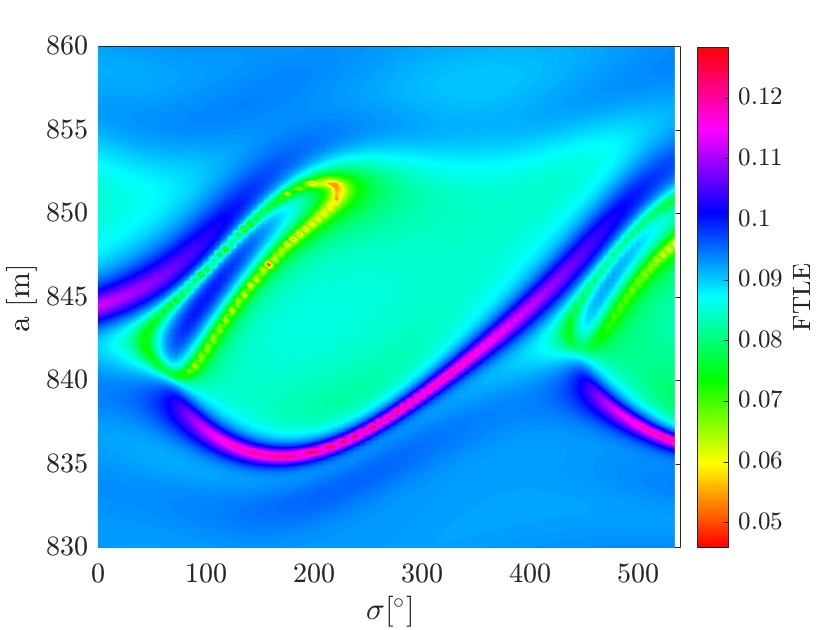
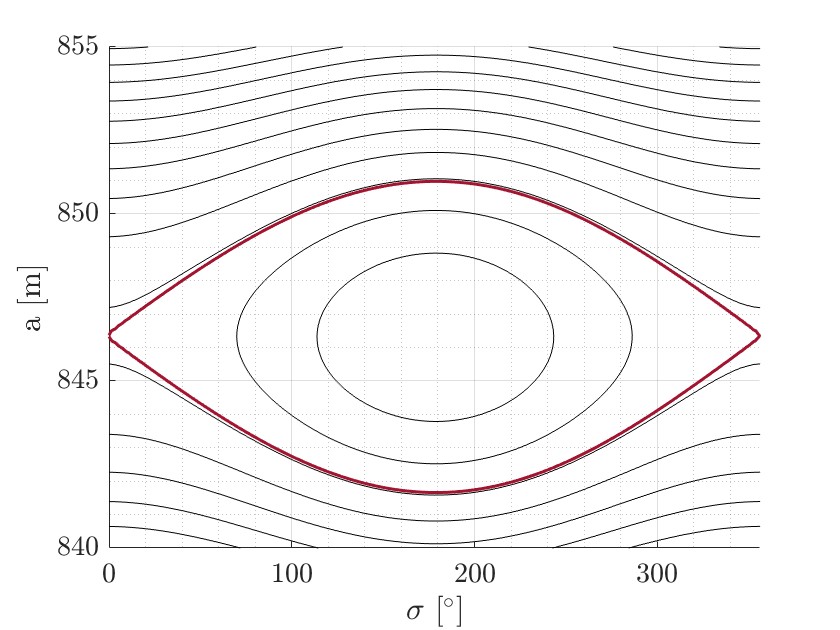
Fig. 1: Comparison between FTLE map (left) and phase-space portrait (right) for the 1:3 p₁ : p₂ resonance.

To investigate how resonances can facilitate the temporary or long-term trapping of particles, this study considers capture mechanisms influenced by perturbations relevant to natural ejecta, such as solar radiation pressure and energy-dissipating effects arising from particle collisions, extending the analysis beyond the typical resonance capture analysis applied to controlled spacecraft trajectories under low-thrust propulsion [5].  Inter-particle interactions are preliminarily modeled via a Stokes-like drag term, used as a simplified proxy for energy loss from mutual collisions.

A Monte Carlo approach is employed to statistically assess the probability of particles becoming trapped within previously identified resonant regions.

The examination of features such as the stabilization of the semi-major axis over time, energy variations near separatrices in the Hamiltonian phase-space, and the behavior of stability indicators, are used to distinguish transient from longer-lived trapping.

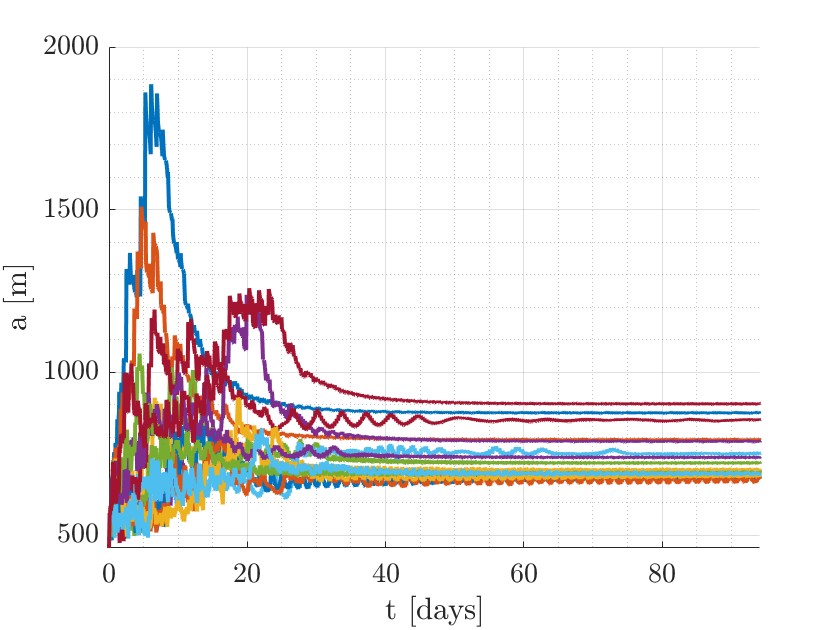
Fig. 2: Evolution of semi-major axis for particle captured in a Monte Carlo simulation with drag-like perturbation. 

Preliminary expectations indicate that collisional dissipation and low-thrust-like forces can facilitate trapping, while SRP, due to its varying direction, likely causes short-lived resonance locking. Further analysis will clarify the timescales and conditions for feasible capture. To complement the analysis, an N-body code designed for granular materials is used to simulate realistic particle collisions and investigate their role in resonant capture. While theoretical models offer insight into the dynamics around non-spherical bodies, collision simulations can provide a valuable counterpart by testing how these processes may lead to capture and possibly to binary system formation.

Acknowledgments

This work is funded by the European Union (ERC, TRACES, 101077758). Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.

[1] D. Scheers et al. “The Fate of Asteroid Ejecta”.

[2] B. Sicardy et al. “The dynamics of rings around Centaurs and Trans-Neptunian Objects”.

[3] Nicolas Delsate. “Analytical and numerical study of the ground-track resonances of Dawn orbiting Vesta”.

[4] C. D. Murray et al. “Solar system dynamics”.

[5] W. Boumchita et al. “The capture probability of Dawn into ground-track resonances with Vesta”.