Regolith dynamics and long term surface evolution on asteroids

Introduction
Small planetary bodies, such as asteroids, have surfaces covered with loose granular material known as regolith. This regolith can flow under disturbances from impacts, tidal interactions, or spin variations caused by thermal torques. The complex gravity field, irregular shape, and potentially three-dimensional rotation of these bodies affect how the regolith flows across the surface. 

We propose a framework to investigate regolith dynamics on small planetary bodies, such as asteroids, over long timescales, focusing on their impact on the body's spin and shape evolution. We begin by examining the idealized case of axisymmetric regolith motion, followed by a generalization to the more complex non-axisymmetric scenario.

Methodology

We assume that the regolith movement is triggered by impact events that induce seismic shaking on the asteroid's surface. To simulate the stochastic history of these collisions, we employ the size frequency distribution of the main asteroid belt. While the majority of the collision energy contributes to crater formation, a smaller portion is transmitted as seismic waves. We propose that regolith flow initiates when seismic waves produce stress levels that surpass the material’s cohesion and hydrostatic compression. Once movement begins, we assume the regolith remains fluidized as long as seismic shaking continues on the asteroid. Our regolith flow model incorporates a rotating frame to account for the asteroid's spin, curvilinear coordinates to capture complex topography, and  mass loss from the surface.

Asteroids typically have irregular shapes, yet top shapes are in plenty. Top shapes can be thought of as minor deviations from a sphere. With this inspiration, we envision the central body to be a sphere with shallow topographical features on its surface that evolves after each landslide. We finally augment the landslide model with the Monte-Carlo collisional history of an asteroid and stochastic thermal/YORP (Yarkovsky–O'Keefe–Radzievskii–Paddack) torque. 

Axisymmetric motion

Regolith motion is neither global nor symmetrical. However, the current section assumes axisymmetric nature of regolith motion to reduce the complexity of the mathematical equations involved.
Figure 1 illustrates the shape evolution of an initially spherical asteroid. Under the influence of a spin-increasing YORP torque, impact-induced landslides drive gradual surface reshaping, causing the asteroid to slowly transform into a top-like shape.

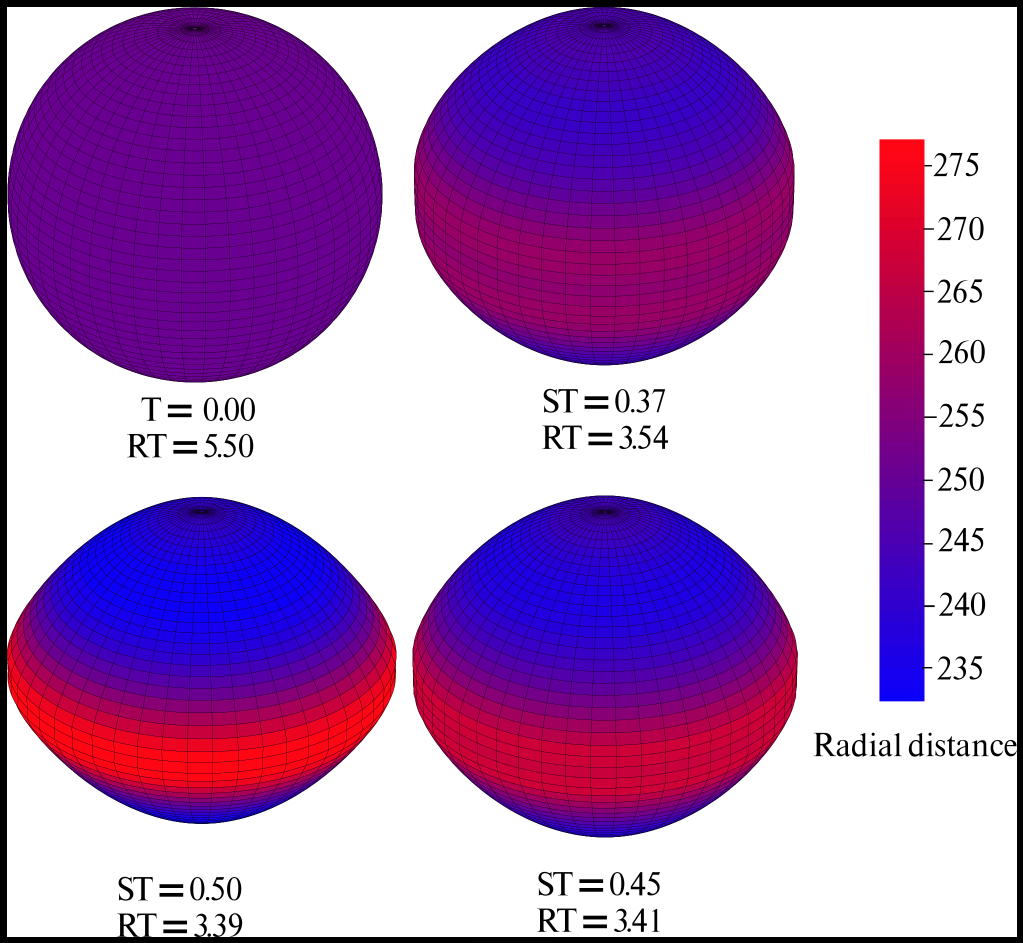
Figure 1: The evolution of shape of an initially spherical asteroid. ST is the simulation time and RT is the rotational time period. Radial distance is the distance of the point from the center of the sphere.

The effects on spin change due to various active processes are shown in Fig. 2. shows the spin change when different processes were considered such as  collision (C), YORP torque (Y) and surface landslides (L). We found that the impact induced landslides can contribute to spin change only at high rotation rates (or small rotation periods).

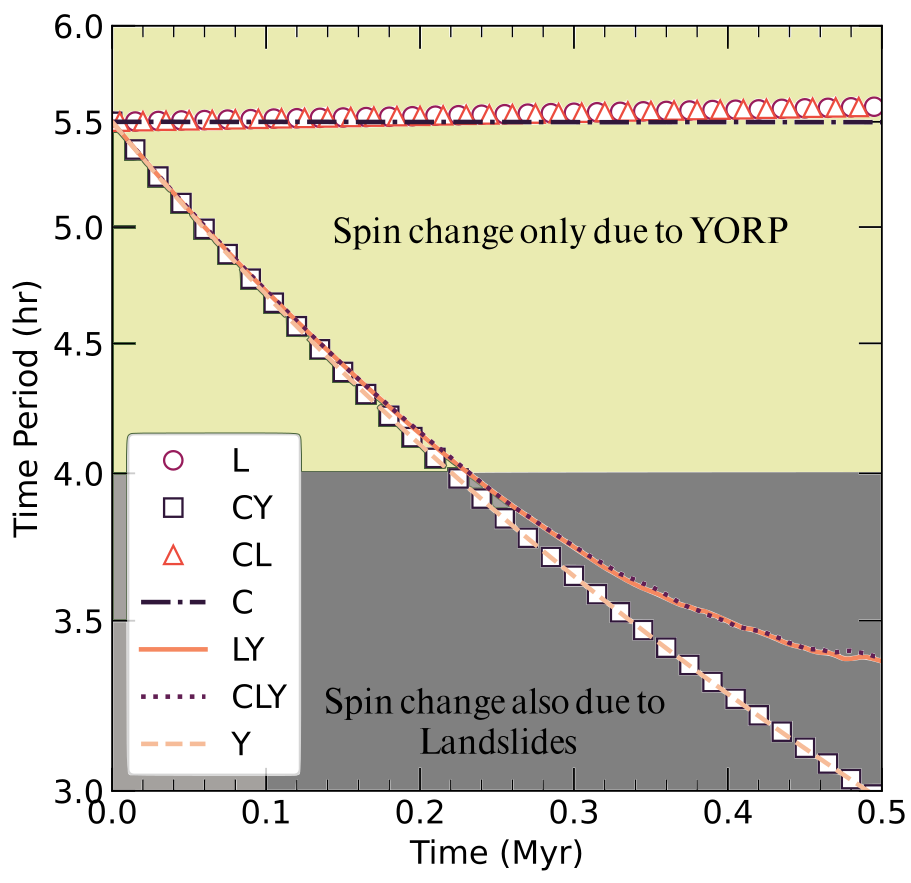
Figure 2: Spin evolution resulting from collisions (C), YORP torque (Y), and surface landslides (L), with all possible combinations of these processes illustrated

Non-axisymmetric landslides

Non-axisymmetric regional scale landslides represent a more realistic scenario. On a fast rotating asteroid, the Coriolis force will dominate the regolith migration. To illustrate this, the slumping of an idealized Gaussian dune on a frictionless spherical asteroid is shown in Fig. 3. In the absence of rotation the dune should slump gradually and its peak remains at the same spot, as gravity is normal to the surface. However, due to rotation, the centrifugal force moves the peak towards the equator while the Coriolis force moves it westward. As the dune reaches the equator, it slows down and begins spreading in the azimuthal direction.

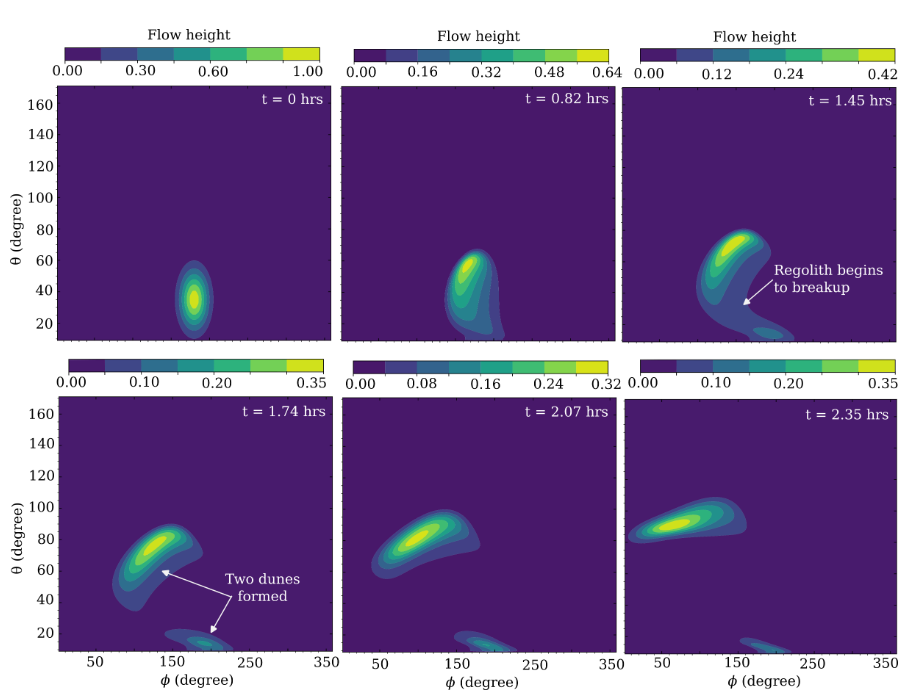
Figure 3: The slumping of a Gaussian dune on a frictionless spherical asteroid. θ is the meridional direction and Φ is the azimuthal direction.

Finally, we simulate dune slumping on a Bennu-shaped asteroid rotating with a short period of 3.4 hours, as shown in Figure 4. Our results show that the regolith does not reach the equator. The prominent equatorial bulge of Bennu acts as a barrier, hindering the material’s movement toward the equator. At such high rotation rates, some of the material begins to lift off the surface and enter orbit

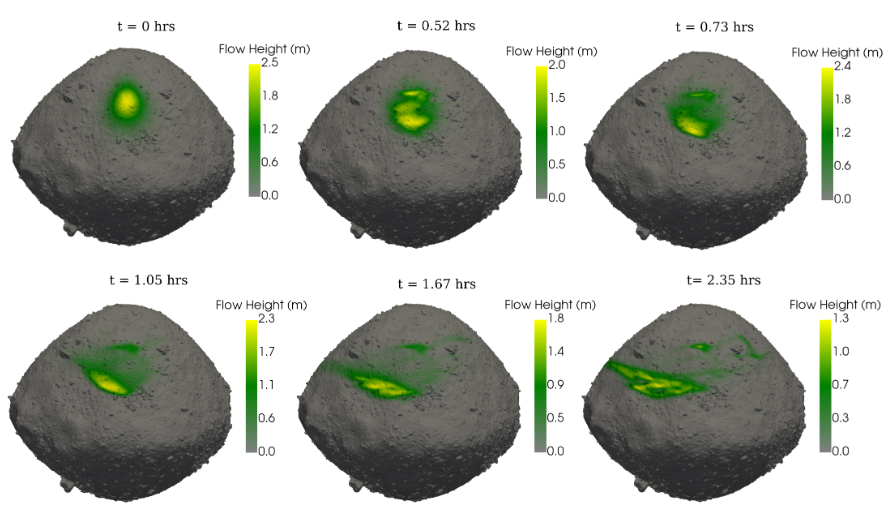
Figure 4: The slumping of a dune on a Bennu-shaped body.

Conclusion

We introduce a framework for analyzing regolith motion on asteroid surfaces, incorporating various active processes affecting the body. We demonstrate its application in an idealized scenario involving axisymmetric regolith flow and find that such motion becomes prominent at high rotation rates, significantly influencing the spin and shape of small planetary bodies. The framework is then extended to model dune slumping in non-axisymmetric cases, including asteroids with shapes similar to Bennu.