Extreme planetary resonances: Study of high eccentricity and high inclination resonances in exoplanet systems

Over the past 30 years, the number of confirmed exoplanetary systems has increased enormously, with nearly a thousand systems hosting multiple planets. The orbital architectures of these systems have challenged traditional formation models and reshaped our understanding of how planetary systems form and evolve. Notably, the observed eccentricity distribution shows that many exoplanets have highly eccentric orbits, in sharp contrast to the quasi circular orbits of the Solar System (SS) planets. Additionally, observations using the Rossiter-McLaughlin effect have shown that some exoplanets orbit in polar orbits relative to their host star’s equator, whereas all planets in the SS orbit within relatively coplanar configuration. These findings highlight the importance of studying the dynamics of inclined and eccentric planetary configurations.

Furthermore, the distribution of period ratios in multi planet systems exhibit clear concentrations near mean-motion resonances (MMRs), which can significantly influence the long-term orbital evolution of such systems. For instance, the system HD 31527 appears to be stable only within the high-order 16:3 resonance. In this configuration, resonance helps prevent close encounters between outer planets, avoiding chaotic zones. In contrast, planets in the SS lie close but out of major resonances. Numerical experiments show that forcing SS planets into resonance typically leads to instability. This could be expected, since formation models suggest that planetary migration can be stopped by resonant trapping, but raises important questions: are planetary resonances stabilizing or destabilizing systems?
The answer depends on the context, much like the case of small body populations in the SS, where some resonances appear as concentrations of objects while others are empty.

It is crucial to understand the structure and properties of individual resonances and how they influence long-term orbital evolution. Generally, classical approaches for calculating the resonant disturbing function were analytical expansions only valid for some interval of eccentricities and inclinations or for particular resonances. However, calculating the resonant function numerically is advantageous as it has no restrictions on orbital elements or type of resonance.

In this work, we apply a semi-analytical model to compute the resonant disturbing function, the Hamiltonian, and the properties of any given resonance between two planets. We are only limited by the fast evolution of eccentricity, inclination, argument of perihelia or longitude of ascending nodes as the model assumes they stay more or less constant during a libration period.The model calculates the resonance width, the location of the equilibrium points and the libration period.

Traditionally, resonances have been classically classified as symmetric if there exists one equilibrium point where the critical angle oscillates around 0° or 180°or as asymmetric if there exists two equilibrium points separated by less than 180°. Most low inclination resonances are symmetric whereas 1:1 and all other 1:N resonances are asymmetric. In this work, we present results from mapping resonance properties in the (eccentricity, inclination) and (inner eccentricity, outer eccentricity) phase spaces. These include new resonant equilibrium points, which we validated through numerical integrations and compared with observed exoplanet systems from available databases.

Finally, we explore how the long-term secular evolution within resonances is affected by high eccentricities and inclinations. Our findings indicate that the phase-space topology of resonances can change dramatically under such conditions, challenging the traditional classification and revealing more complex dynamical structures.

Figure 1: Standard deviation of the number of equilibrium points for the 2:3 resonance in the (e, i) plane varying ω.

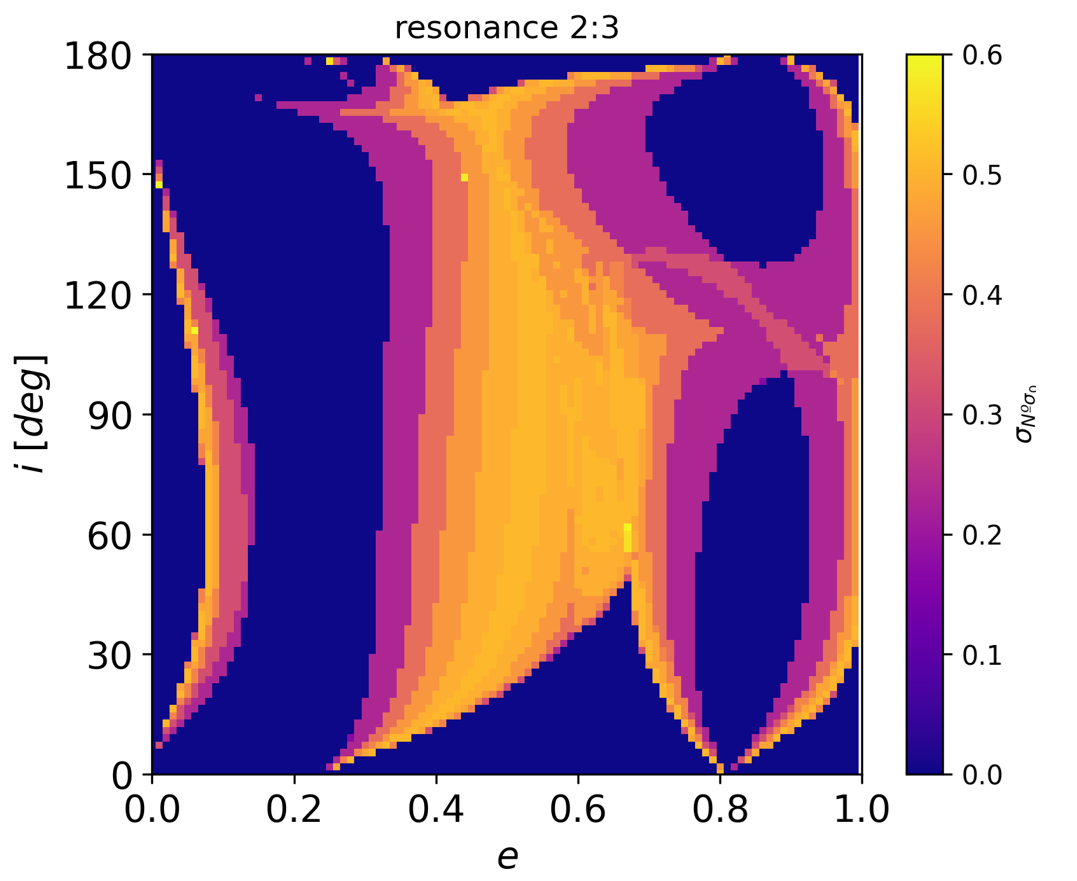
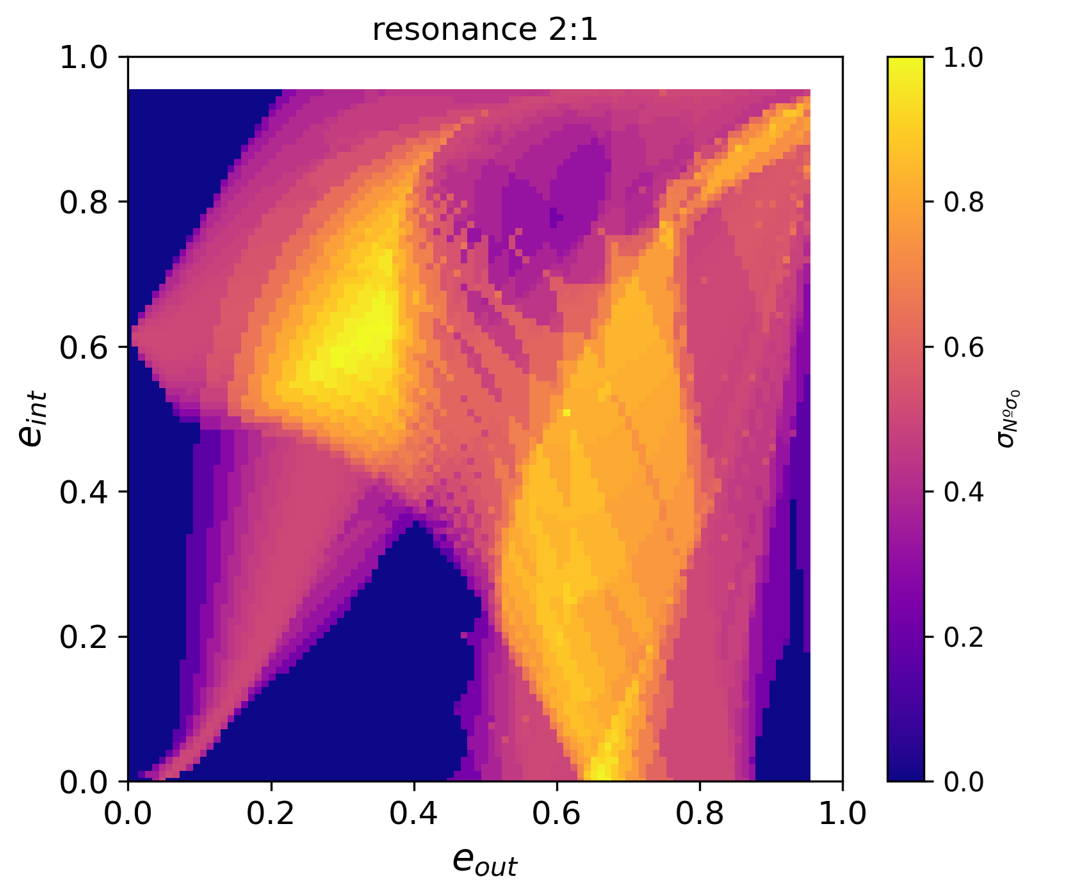
Figure 2: Standard deviation of the number of equilibrium points for the 2:1 resonance in the eccentricities plane varying ∆ω.