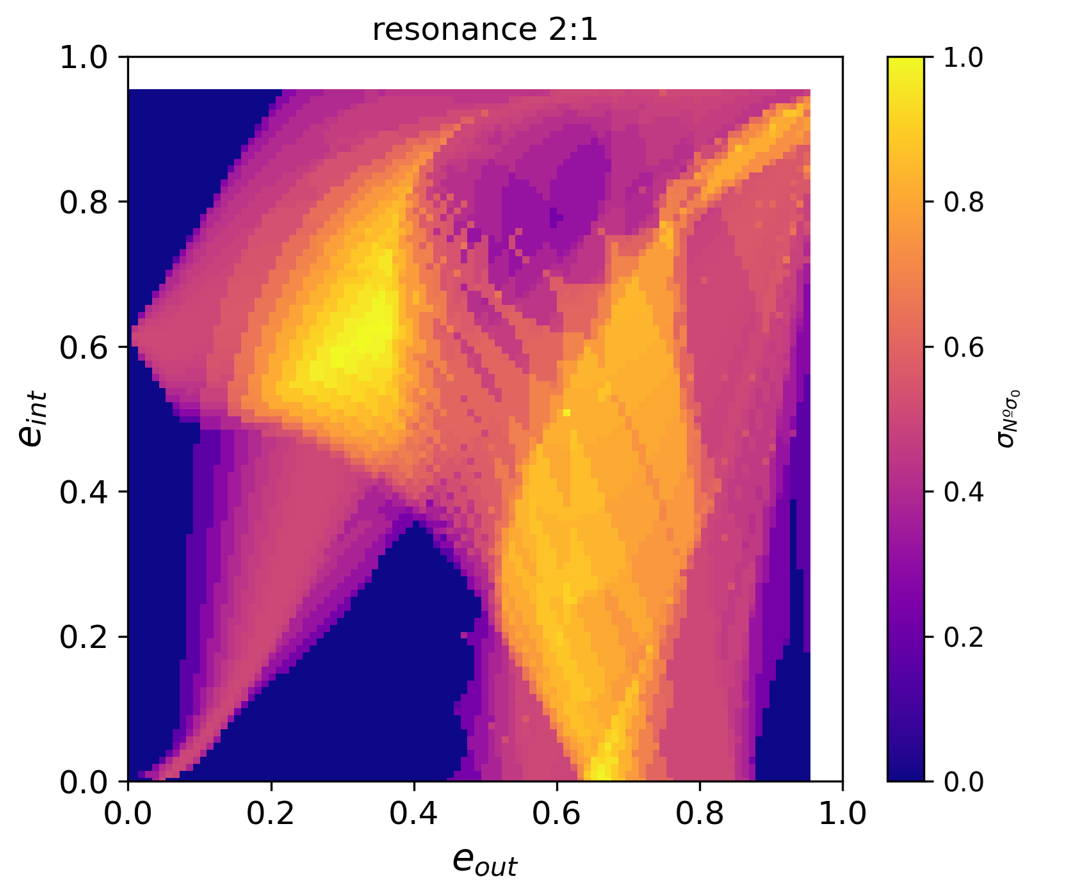
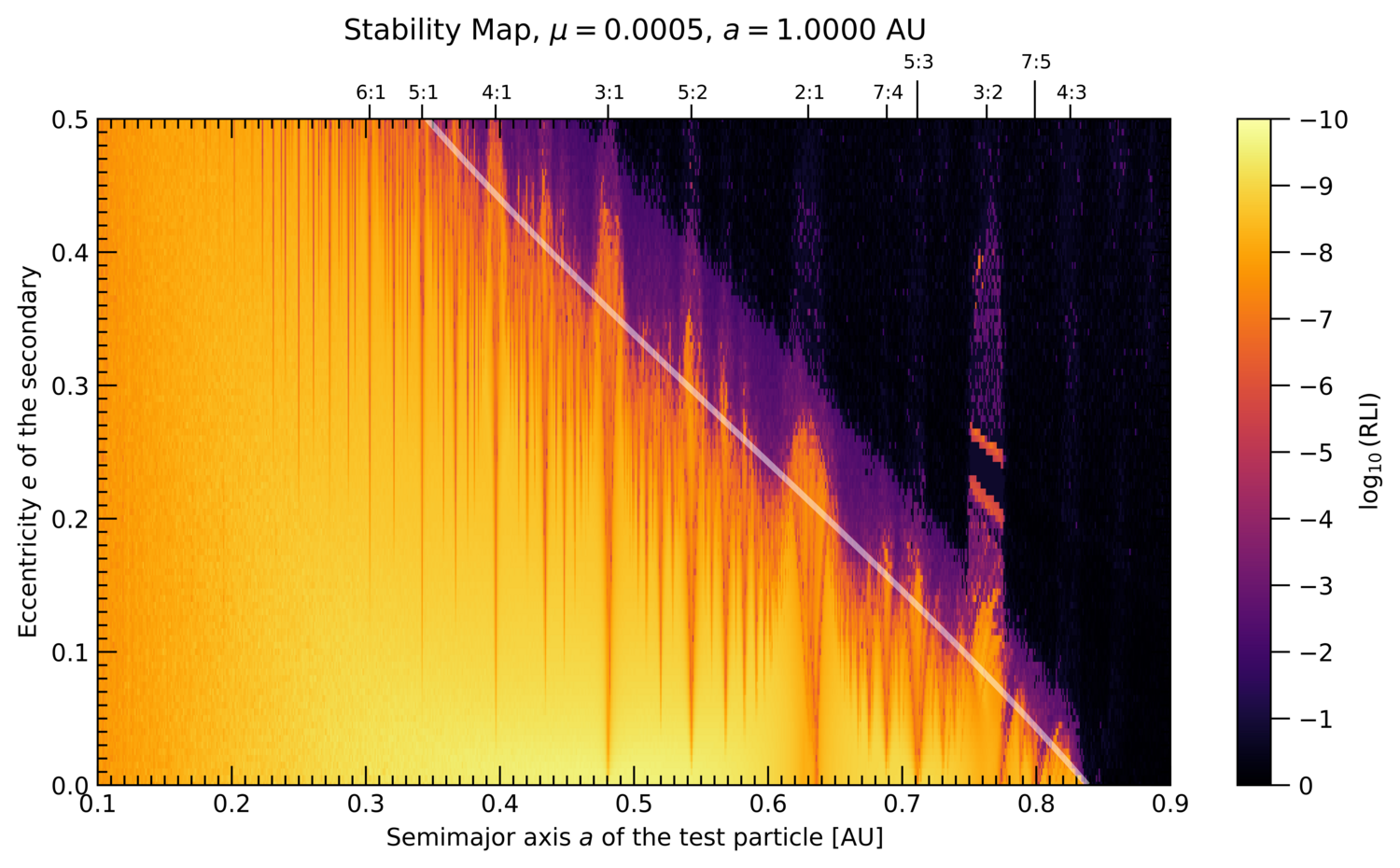
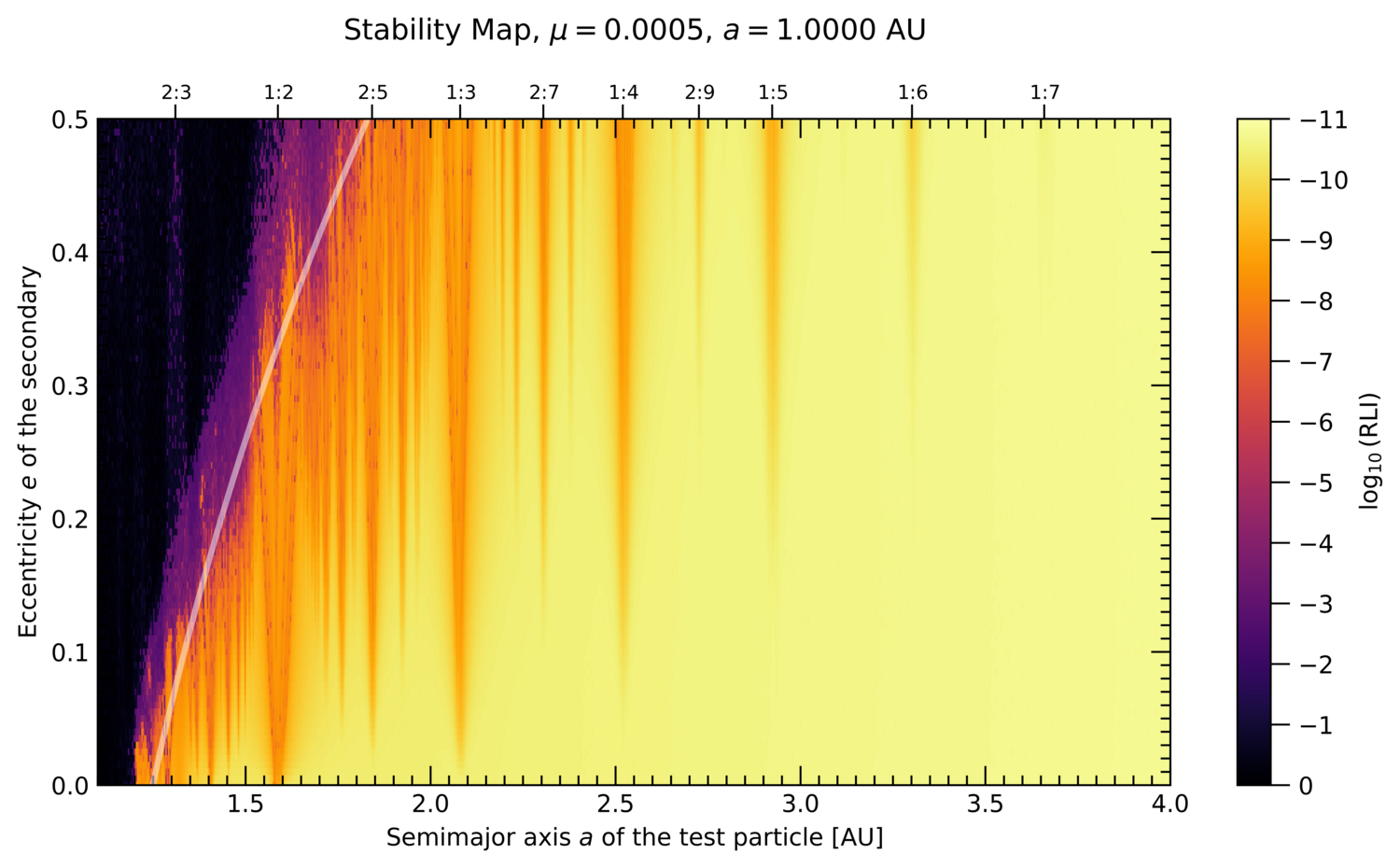
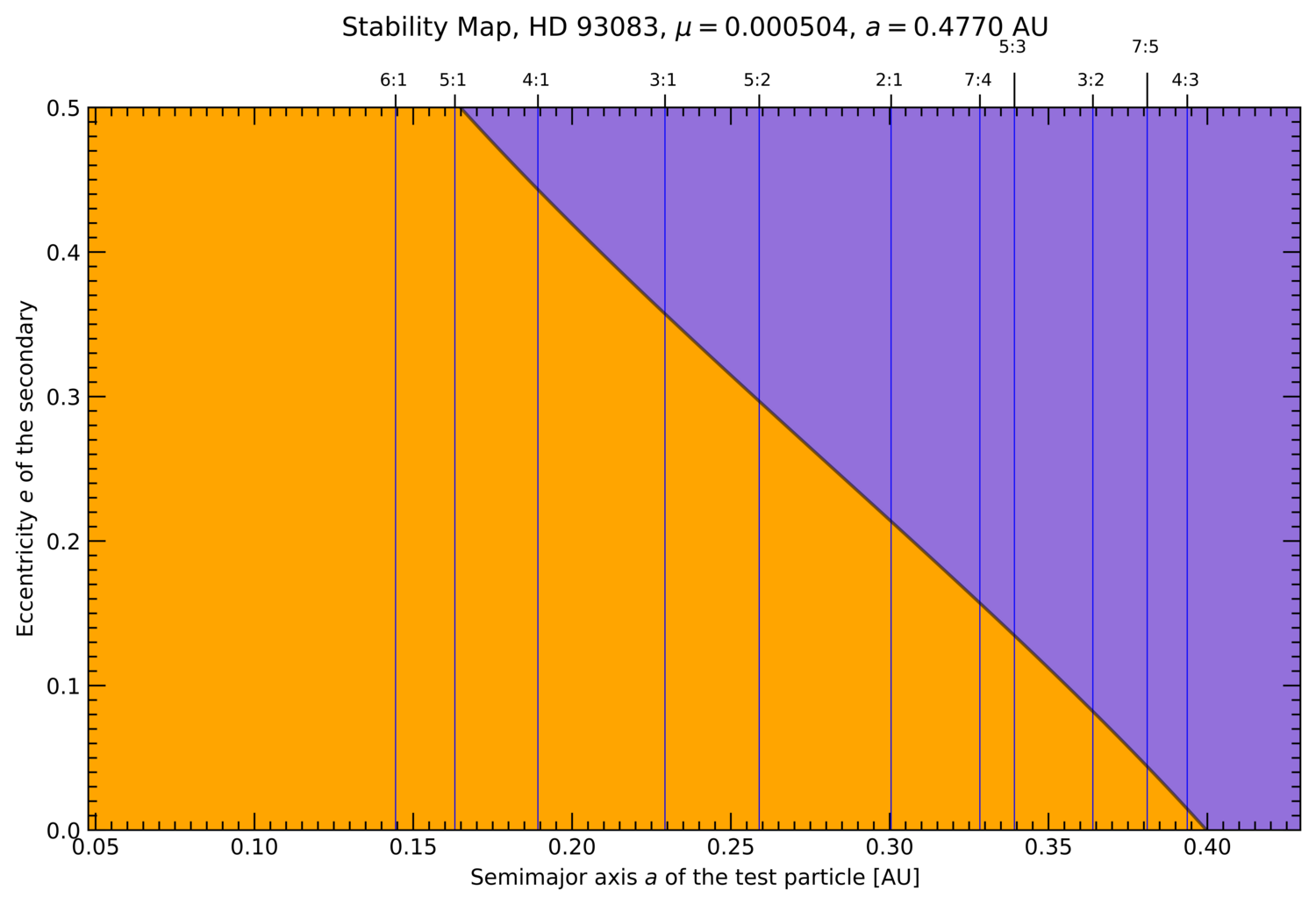
EXOA17

The number of known planetary systems continuously grows, revealing an increasingly complex nature of extrasolar worlds, challenging our understanding of planetary system formation and evolution.

In this session, we address the question of the intricate dynamical evolution of RV-detected systems and transit-detected planetary systems, where resonant and chaotic processes emerge from complex gravitational interactions. Additional effects, including tidal forces, general relativistic effects, planet-disc interactions, and the gravitational influence of binary companions, can strongly affect the architecture and long-term stability of such systems.

This session aims to explore how theoretical modeling can provide crucial insights into system characterization by confronting dynamical predictions with observational constraints, highlighting how dynamical constraints inform our interpretation of planetary system architectures from initial formation to long-term evolutionary states.