WARPE: A new tool to simulate radiative transfer and travel-time to characterize planetary surfaces

Introduction

The next generation of lidar instruments will encompass the full waveform recording, allowing travel-time measurement of each emitted photon packet. This new information will allow finer characterization of planetary surface medium, either spaceborne, in-situ or in lab; for instance, the BepiColombo laser altimeter (BELA) (Thomas et al., 2021) will explore Mercury. We propose here a tool to simulate in-silico the travel-time inside the planetary medium and reconstruct the full waveform. It is a Monte-Carlo ray tracing algorithm called WARPE, for Waveform Analysis and Ray Profiling for Exploration (Barron et al, 2025).

Methods

We propose a Monte Carlo ray tracing approach based on the work from Farrell et al., 1992, Wang et al., 1995 and Gastellu-Etchegorry et al., 2016. Our model computes the position of the ray during its travel through the medium, including interactions at the interfaces. The main parameters are incidence (θ) and azimuthal angle (φ), the optical thickness (τ), the single scattering albedo (ω) the optical index (n,k) of the medium and the phase function (Henyey-Greenstein or isotropic). The efficient computation time of the model is guaranteed by ray batchs parallelization.

Validation

The validation of the model is a mandatory step to compute a consistent and physically correct simulation of the travel-time within a planetary surface. In the model, media can be either described as a semi-infinite granular layer or a homogeneous slab above a bedrock or regolith of albedo (A). The purpose here is to replicate the results from previous works such as Stamnes et al., 1988, Gautheron et al., 2024 and Kienle & Patterson 1997. We first computed the reflectance for a turbid medium with (figure 1) and without (figure 2) interfaces. We use the DISORT algorithm (Stamnes et al., 1988) and the model presented in Gautheron et al., 2024. Our simulations show a very good agreement, confirming the validity of WARPE for angular distribution. The Relative Root Mean Square Error (RRMSE) is ∼ 0.01 in most of cases, which is excellent and expected due to the stochastic nature of WARPE.

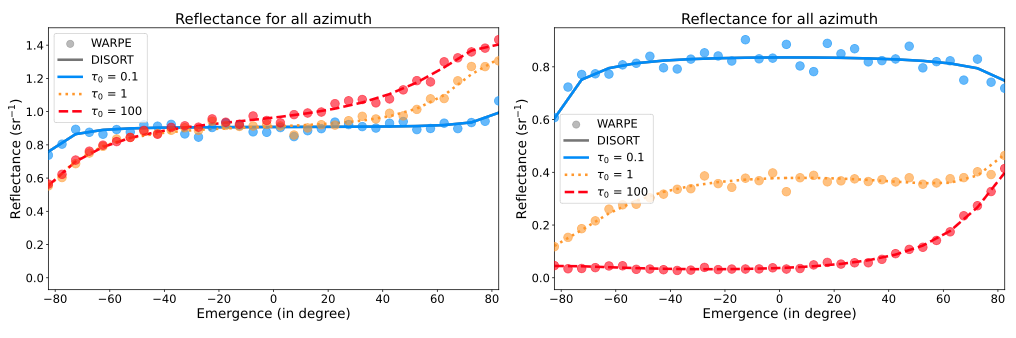
Figure 1: Reflectance of a turbid medium with WARPE (point) and DISORT (line) for θ = 50°. ω = 1, A = 0.9 (left), ω = 0.7, A = 0.9 (right). The diffusion is anisotropic following a 1-parameter Henyey-Greenstein phase function with g = 0.8.

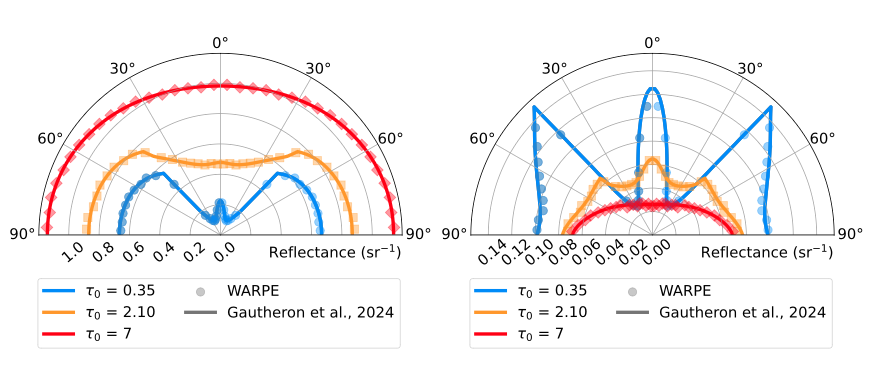
Figure 2: Reflectance from WARPE (points) and from the Gautheron et al., 2024 model (lines) within the medium at the top interface, as a function of emergence for with ω = 1 on the left and ω = 0.7 on the right, n = 1.5. The diffusion is anisotropic and follows a 1-parameter Henyey-Greenstein phase function (with g = 0.8).

 

We propose then a method to compute the trajectory and travel-time of rays in the medium, to simulate the response of a waveform lidar. Knowing the speed of light in the medium and assuming its constancy following medium’s optical properties, we then evaluate the time travel in comparison with the analytical solution from Kienle & Patterson, 1997. Results in Figure 3 shows a very good agreement that validates our algorithm.

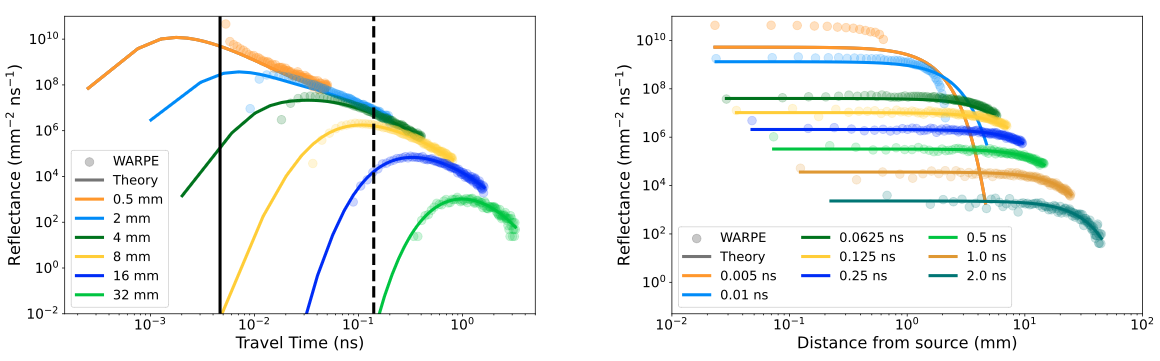
Figure 3: Reflectance in a compact medium from WARPE (point) and analytical model from Kienle & Patterson (1997) model (line); (left) as a function of travel-time at distance from the source; (right) as a function of distance from the source at different time. Parameters are τ = 60, n = 1.4 and k = 0, z₀ = 0.995 mm and t₀ = 4.67 ps. The diffusion is isotropic (g = 0), the approximation for the anisotropic diffusion being too imprecise in the Kienle analytical model. The full vertical line represents the travel-time at t₀ =  z₀ /n to leave the medium in a straight path without interaction, when the source is at depth z₀ . It is thus not physically possible that a travel-time shorter than this exists. Our model fulfills this condition, but the analytical solution does not. The dash vertical line represents the time from which WARPE and reference model reasonably agree (after ∼ 30t₀ ). 

 

Result

To illustrate the capabilities of WARPE, we simulate waveforms for different sets of parameters. We identified 4 main features: the top reflection corresponding to specular reflection, the back and forth direct represents rays unscattered in the medium but reflected 1/2/3… times in the bottom and top interfaces, the back and forth diffused represents the “pseudo-wave” of all scattered rays and finally the background scattering. Figure 4 shows the effect of the optical thickness and how the features are affected. We are now able to identify how the media properties will affect the response of a full waveform lidar.

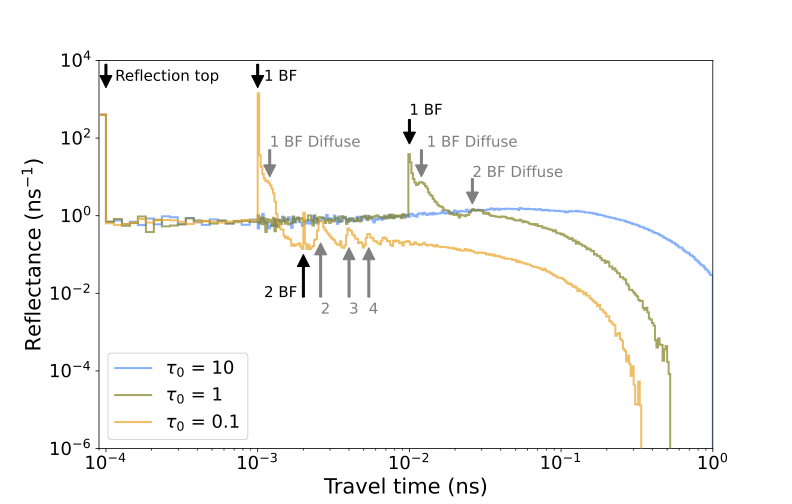
Figure 4: effect of the optical depth  on the travel-time. Parameters θ = 0°, ω = 1, A = 0., n = 1.5, rand a Henyey-Greenstein phase function with a scattering anisotropy of g = 0.8, scattering coefficient is 1, absorption coefficient is 0. The physical thickness is 0.1 (orange) 1 (green) 10 (blue) mm. The back and forth direct (BF) and the back and forth diffuse (BF Diffuse) features are more visible when the medium is optically thin. For thicker medium the main feature tends to be the background scattering.

 

Conclusion and perspectives

We propose a new approach to efficiently simulate the travel-time of photons inside a planetary surface with both granular and compact texture. We conducted several tests to validate the approach and one simulation in realistic conditions. In the future, we will adapt this tool to peculiar planetary science cases, such as the mercury regolith for BELA, or the icy surface for GALA.

 

References

Barron et al. (2025) under review Journal of Quantitative Spectropy and Radiative Transfer

Farrell et al. (1992) Medical Physics

Gastellu-Etchegorry et al. (2016) Remote Sensing of Environment

Gautheron et al. (2024) Optics Express

Kienle et al. (1997) Journal of the Optical Society of America

Stamnes et al. (1988) Applied Optics

Thomas et al. (2021) Space Science Reviews

Wang et al. (1995) Computer Methods and Programs in Biomedicine