Using Gaia to reduce atmospheric turbulence displacements in LSST minor planet astrometry

The imminent start of LSST will trigger an unprecedented advance in the discovery and precise tracking of small solar system bodies. The survey is expected to yield order-of-magnitude increases in known population sizes, and to produce hundreds of observations of each target during its 10-year duration. The nominal astrometry requirement is 10 mas RMS errors per visit, a level where unmodeled displacements are dominated by atmospheric turbulence. We present a new code that interpolates, with Gaussian process regression (GPR), the turbulence displacement field on any ground-based telescope exposure that includes enough stars from Gaia DR3, using the computed displacement at the position of these stars. This idea was initially laid forth by Fortino et al. (2021), who tested a preliminary method on a few Dark Energy Survey (DES) exposures. Their code required optimization of the Gaussian process kernel, and therefore was too computationally expensive to be scalable for future surveys such as LSST. We approach the problem by generating empirical kernels: the correlation function of the turbulence field is measured directly with TreeCorr (Jarvis 2015) and smoothed to avoid numerical issues.

 

Our code roughly follows these steps: (1) Find stars on the exposure that have close matches to Gaia solutions; (2) compute the displacements in both directions for each reference star—these directions are treated as independent fields; (3) perform a polynomial fit to model large-scale correlations, remove outliers from the reference star set; (4) measure the correlation function of polynomial-subtracted displacements with TreeCorr; (5) reduce noise and apodize the measured correlation function to generate the GPR kernel; (6) divide exposure in patches and perform a GPR on each patch to get a modeled turbulence displacement value on the target positions (that is, the position of every star on the exposure that does not have a match in the Gaia catalog). An initial run may be done to detect additional outliers from the reference set, have them removed, before a second and final GPR run. 

 

For cross-validation purposes, we divide the reference star set into five subsets, and perform five GPR runs, each with one of these sets reserved as targets. We then use the model-subtracted residuals at these targets to estimate the remaining unmodeled turbulence. We test our code both on real DES exposures and on simulated LSST data (where turbulence is generated by the atmospheric model from Hebert (2024)). Using the average correlation function for separations < 1’ (ξ₀) as a metric for the variance of turbulence distortions, we compare its raw value with the model-subtracted one and we find that it is reduced by an average factor of 12.2 on the DES exposures. The pre-GPR and post-GPR values for the tested exposures are shown in Figure 1. For the LSST simulations (where the “true” displacements are accessible to us), we compute the true variance of the displacement fields before and after the GPR, and the reduction factor is 13.8. The square root of these values (3.5 and 3.7 respectively) provide us the expected improvement on the RMS of turbulence displacement errors.

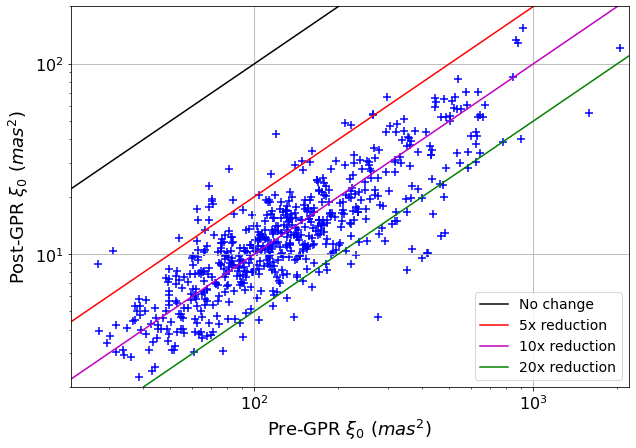
Figure 1. Post-GPR (model subtracted) average correlation function for separations < 1’ versus the corresponding Pre-GPR value. Each blue point denotes one DES exposure where the turbulence reduction code was tested.

 

We then look at the potential use of our code to improve LSST minor planet astrometry. We consider a set of ~1000 main belt asteroid orbits and predict all their detections on a baseline LSST simulated survey. For each detection, we compute the estimated astrometric errors with and without turbulence reduction. The total error is a combination of the photon-noise error and a fixed astrometric floor that accounts for turbulence and remaining calibration errors. This astrometric floor is set at the pre-GPR nominal value of 10mas for the uncorrected scenario, and at the post-GPR value of 2.5mas, the typical value achieved on simulated LSST fields, for the corrected scenario. We find that the total positional information on MBA orbits (defined as ∑ 1/(σ_i)² for i observations) improves by a factor of 13.3 (for asteroids with H < 16) and by a factor of 5.4 for H > 16.  Figure 2 shows the positional information for each object after the 10-year survey, in both scenarios (corrected and uncorrected). Fainter asteroids have a larger contribution of photon-noise error and therefore are less affected by the turbulence reduction.

Figure 2. Total positional information expected after 10 years of LSST, for a sample of ~1000 Main Belt Asteroids. Blue points represent the scenario where no turbulence correction is applied (10mas errors added in quadrature to the photon noise error). Red points reduce the astrometric errors according to the performance of our turbulence reduction code (the astrometric floor is moved from 10mas to 2.5mas).

The information gain from Gaia-referenced turbulence reduction will translate into more precise orbital constraints for a given number of measurements, improving sensitivity to signals such as non-gravitational forces, small deflections from mutual encounters, and gravitational perturbations from unmodeled mass in the Solar System.

 

References

 

Fortino, Willow. F., Bernstein, Gary M., Bernardinelli, Pedro H., et. al. 2021. "Reducing Ground-based Astrometric Errors with Gaia and Gaussian Processes." The Astronomical Journal 162 (3): 106. https://doi.org/10.3847/1538-3881/ac0722.

Hébert, Claire-Alice, Meyers, Joshua E., Do, My H., et. al. 2024. "Generation of Realistic Input Parameters for Simulating Atmospheric Point-Spread Functions at Astronomical Observatories." The Open Journal of Astrophysics 7 (April): 22. https://doi.org/10.33232/001c.115727.

Jarvis, Mike. 2015. TreeCorr: Two-point Correlation Functions. Astrophysics Source Code Library, record ascl:1508.007. https://ui.adsabs.harvard.edu/abs/2015ascl.soft08007J.