Enforcing multiple constraints on the interior structure of Ganymede: a machine learning approach

Introduction:  Determining the internal mass distribution of planetary bodies, such as Ganymede, remains a challenging problem due to observational degeneracies. In the 2030s the JUICE mission with its several instruments will orbit Ganymede and provide information on parameters that depend on the interior structure of the moon, including estimates of the polar moment of inertia, the radial and gravitational Love numbers and associated phase-lags, the longitudinal libration amplitudes, as well as the phase and amplitude of the induced magnetic field due to the presence of a subsurface ocean. In order to impose the constraints on the interior structure in the most effective way a joint inversion of all available parameters is ideally  necessary. In this work, we use a machine learning approach  to predict the thicknesses and densities of Ganymede's internal layers and ocean conductivity using these parameters. To achieve this,  a synthetic dataset of  plausible internal structure models of Ganymede is generated via Monte Carlo sampling. For each of these internal structures we compute the corresponding observable parameters (Love numbers, libration amplitude, polar moment of inertia, etc.) using existing  models. We then train a Neural Network on the synthetic dataset to learn the intricate relationships between these parameters and the internal structure model. 

Our model is able to retrieve the internal structure parameters with varying levels of accuracy across different layers, with promising  performance in the prediction the icy shell and ocean thickness and density, ocean conductivity and  thickness of the high-pressure ice layer. The Monte Carlo dropout method is utilized to estimate the uncertainties in the predicted parameters. These results highlight the potential of machine learning as a preliminary and fast tool to detect families of interior structures compatible with the observed parameters. 

 

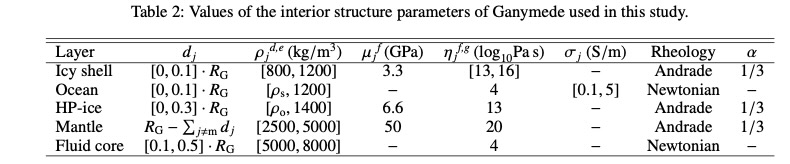
Interior Structure Model: The interior of the icy satellites is modeled as several spherically symmetric, uniform shells and is completely specified by the values of radius R_i, density ρ_i, rigidity µ_i, and viscosity η_i of each layer. The five layers are: an icy shell, a liquid subsurface ocean, an High-Pressure-ice (HP-ice) layer, a silicate mantle and a solid inner core.  For the solid layers we adopt an Andrade rheology, while the ocean and liquid core are treated are treated as inviscid fluids. 

Figure 1: schematic representation of the an internal structure model for Ganymede with five layers.

Dataset and training:  we trained the Neural Network on a synthetic dataset consisting of 10⁷ interior structures, that we generated by performing a Monte-Carlo sampling of the internal structure parameters y, namely: thicknesses and densities of each layer,   icy shell viscosity and ocean conductivity, subject to the total radius and mass constraints. For each interior structure we then computed a set of observables x, including the polar moment of inertia, the radial and gravitational Love numbers h₂ and k₂ using the ALMA³ code [1], the libration amplitude L_s at the orbital period [2], as well as the amplitude A and phase φ_A of the induced magnetic field at the orbital period [3]. 

Neural Network architecture. A schematic representation of the Neural Network is shown in Fig. 2.  The minimization of the loss function is performed using Adam optimizer [5]. In order to prevent any issues with model overfitting we adopt early stopping [6]. We train the neural network with 80% of the data set and use the remaining 20% for validation.

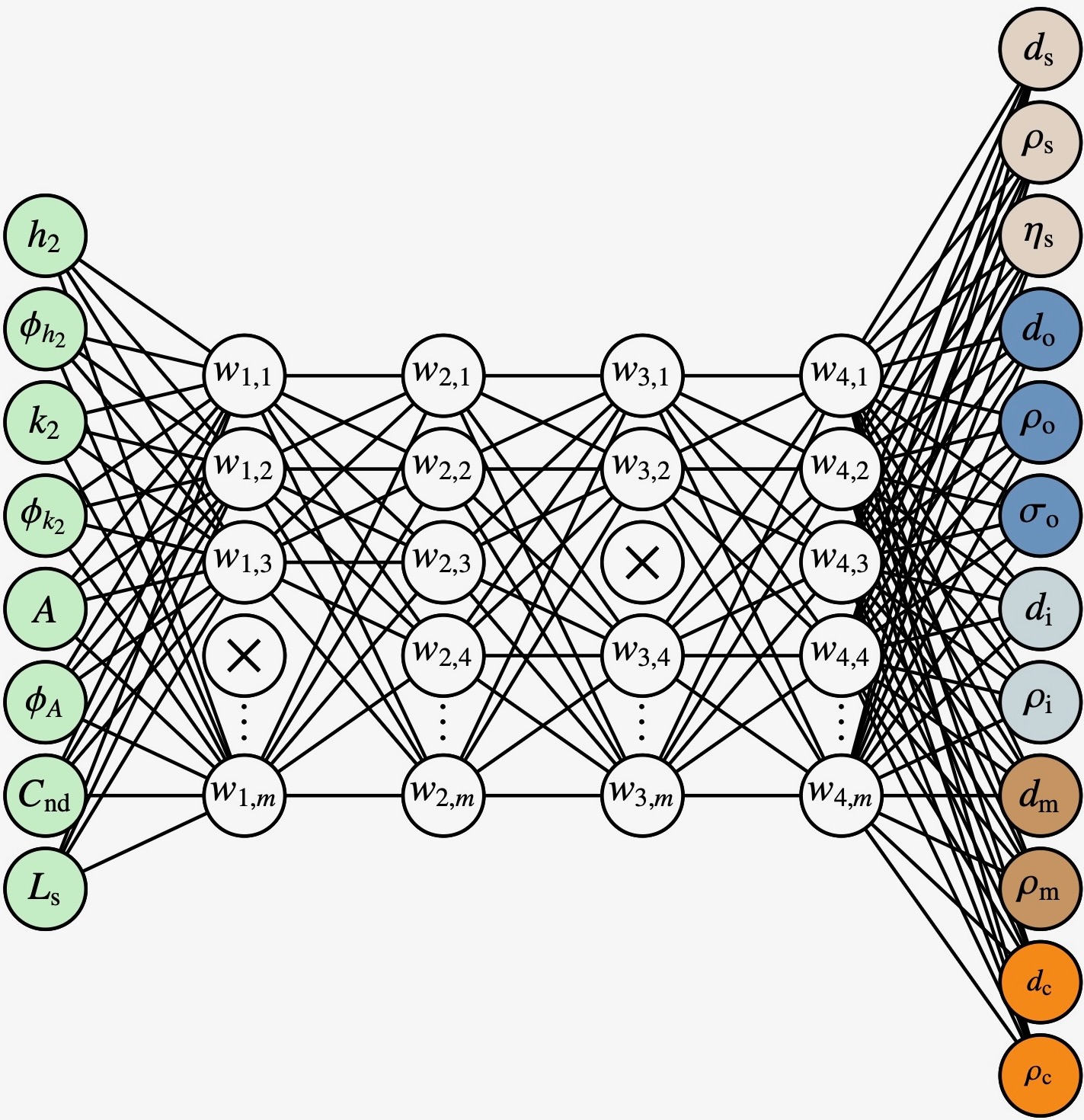
Figure 2: schematic representation of the neural network

Montecarlo dropout. In order to capture the uncertainty in the predicted parameters it would be desirable to have a posterior distribution of the interior structure parameters, rather than deterministic values. To do this we use the Montecarlo dropout approach [7], which allows to obtain an approximate Bayesian inference through dropout training. 

Results and Conclusions:  Our model demonstrates significant predictive accuracy in estimating the thickness and density distributions of Ganymede like icy satellites across its five-layer interior. In Fig. 3, we show a comparison between the actual values of the interior parameters y and those predicted by our trained neural network for the validation dataset y. A perfect prediction would fall on the green dashed line. From the validation dataset, the neural network effectively captured the characteristics of the icy shell and ocean, with excellent agreement between predicted and actual values. The HP-ice layer’s thickness was predicted with moderate accuracy, while its density estimates showed higher variability. The model performs poorly in the task of inferring the thickness and density of the core and mantle, suggesting limited sensitivity of the selected observables to these parameters. However, this had to be expected, and is in line with previous results present in the literature. 

 In Fig. 4 we show the posterior distributions obtained with the Montecarlo dropout method corresponding to the set of parameters x* drawn from the synthetic dataset. We observe that the true values of the internal structure parameters y*, shown as dashed vertical lines, fall within the posterior distributions, close to the mean values in the case of the icy shell, the ocean, and HP-ice layer. However, the methodology presented here come short in the task of assessing the uncertainty in the deeper interior, as the intrinsic degeneracy in the inverse problem allows for a broader range of deep interior structures than those predicted by the neural network.

 

Figure 3.  

Figure 4.  

References:  [1] Melini D., et al., 2022, Geophysical Journal International, 231, 1502 [2] Baland R.-M., Van Hoolst T., 2010, Icarus, 209, 651 [3] Vance S. D., et al., 2021, Journal of Geophysical Research: Planets, 126, [4] Srivastava N., et al., 2014, Journal of Machine Learning Research, 15, 1929  [5] Kingma D. P., Ba J., 2014, CoRR, abs/1412.6980 [6] Prechelt L., 1998, Neural Networks, 11, 761 [7] Gal Y., Ghahramani Z., 2016, in Balcan M. F., Weinberger K. Q., eds, Proceedings of Machine Learning Research Vol. 48.