A Preliminary Study of a Dynamical System Approach to Asteroid Gravity Inversion for Interior Estimation

Accurately modelling the internal density distribution of small bodies such as asteroids is essential for spacecraft navigation, scientific exploration, and planetary defence strategies. Reconstructing the density distribution from external measurements, known commonly as the “inverse gravity problem”, is a challenging problem due to its intrinsically ill-posed nature: different density distributions can yield functionally identical values for a given set of externally observable parameters, whether that is gravitational potential or Stokes coefficients from spacecraft induced accelerations, to name just a few. Furthermore, the solution is highly sensitive to the initial choice of density distribution, often causing the inversion to be dominated by biases from this starting estimate rather than tending towards the asteroid’s true internal structure.

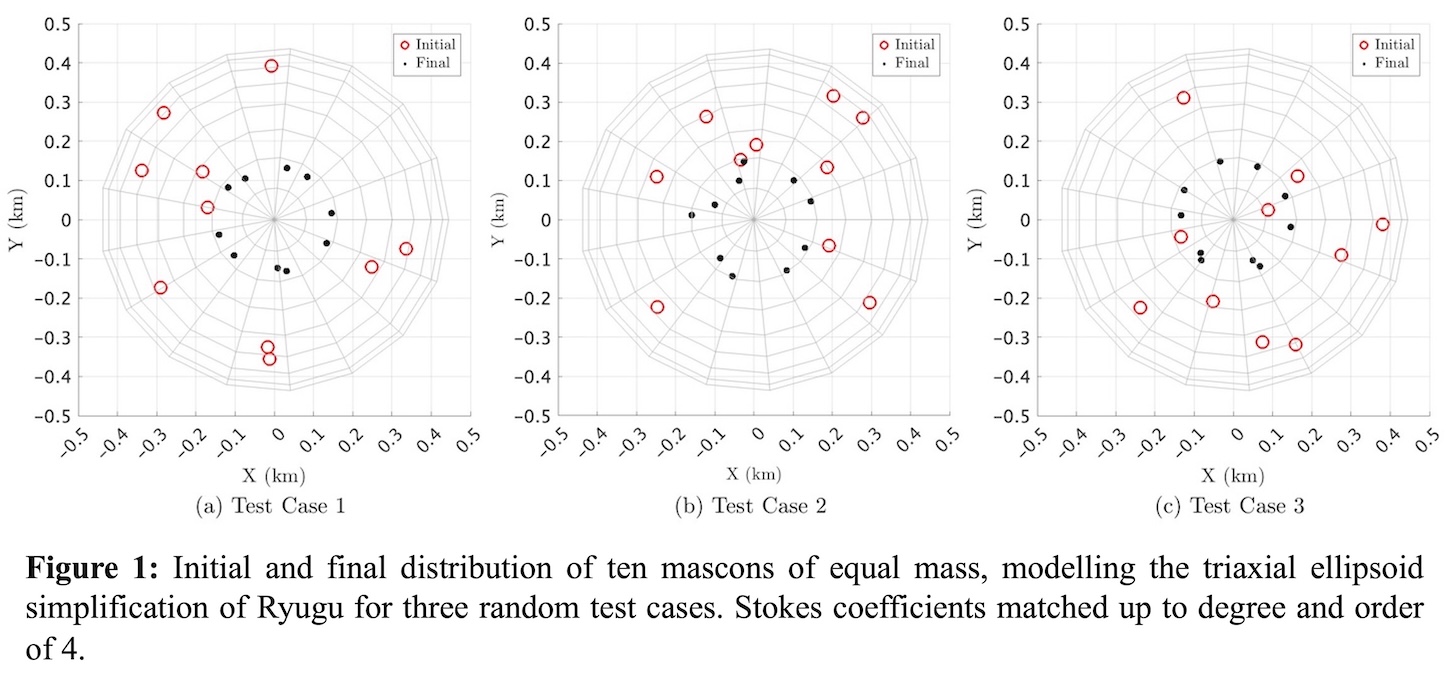
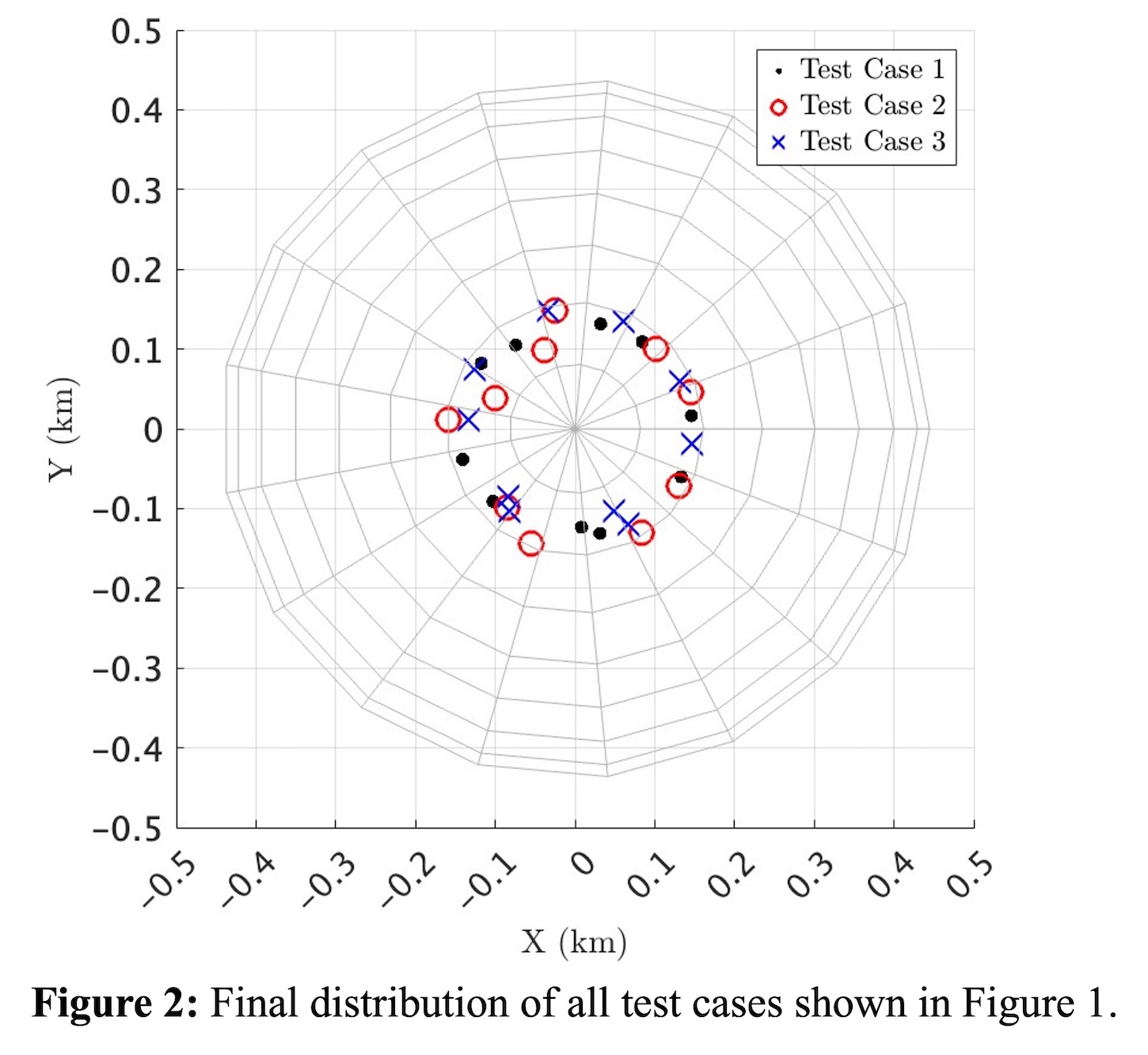
Figure 1 shows this: for three separate initial distributions, the inverse gravity problem was carried out through an iterative least squares algorithm [1], adjusting the location of the mass concentrations (mascons) to minimise the residuals between the modelled Stokes coefficients and that of the “true” model. Despite the modelled Stokes coefficients for each test being the same within immensely small tolerances, the final distribution of each case is very different, thus displaying the issue of non-uniqueness in the gravity inversion problem, albeit for a very simple case. This is shown more clearly in Figure 2, wherein all the final distributions for the same three test cases are plotted on the same set of axes.

 

Addressing this issue of non-uniqueness typically involves imposing additional constraints to limit the number of feasible solutions. These constraints often come from observational data; for instance, ground-based observations such as photometry and radar measurements can refine the shape model and topography [2, 3]. Beyond surface characteristics, constraints on density distribution may also be introduced through estimations of the centre of mass [4], bulk density, and porosity. Although constraints based off this information certainly narrows down physically plausible solutions, it still leaves a range of possible distributions [5], highlighting the need to explore novel approaches for imposing further constraints. Restricting the solution based off these physical parameters has been widely explored; however, the incorporation of dynamical system theory principles has not been explored as extensively. The idea of using equipotential surface to inform the density distribution has been investigated [6], but, as of yet, utilising equilibrium points remains overlooked. Equilibrium points are locations wherein the gravitational and centrifugal forces of a body balance, potentially allowing debris and small particles to linger. In future, thanks to asteroid exploration missions, such points may be observationally detected, either through tracking debris or analysing spacecraft trajectories, thereby providing direct observational data to refine density distribution models.

This study presents a preliminary investigation into whether additional dynamical information- specifically, the location of equilibrium points- can effectively constrain the gravity inversion problem. The main hypothesis is that the locations and characteristics of equilibrium points are sensitive indicators of the underlying density distributions, offering novel dynamical constraints capable of reducing the range of feasible solutions. Initially, the sensitivity of equilibrium points to small variations in asteroid internal density distributions is explored, building upon prior foundational work [7] which indicated that equilibrium point locations shift in response to density changes, highlighting their potential to differentiate between competing density models.

Both forward and inverse methodologies are used to explore this hypothesis in a two-stage study, outlined schematically in Figure 3. Firstly, direct gravity modelling is performed using mascons to represent the internal structure of asteroids with varying density distributions. From these models, the corresponding equilibrium points are calculated. Secondly, the inverse problem is carried out, aiming to reconstruct the original density distributions, taken to be the “true” distribution, using the location of the equilibrium points as additional observational constraints. The results obtained from the unconstrained gravity inversion and the results derived from inversions constrained explicitly by equilibrium point data for the same initial density distribution are then evaluated. This allows a comparison of final distributions assumed by each algorithm, as well as how including equilibrium points affects the sensitivity of the final density distribution is to the initial conditions.

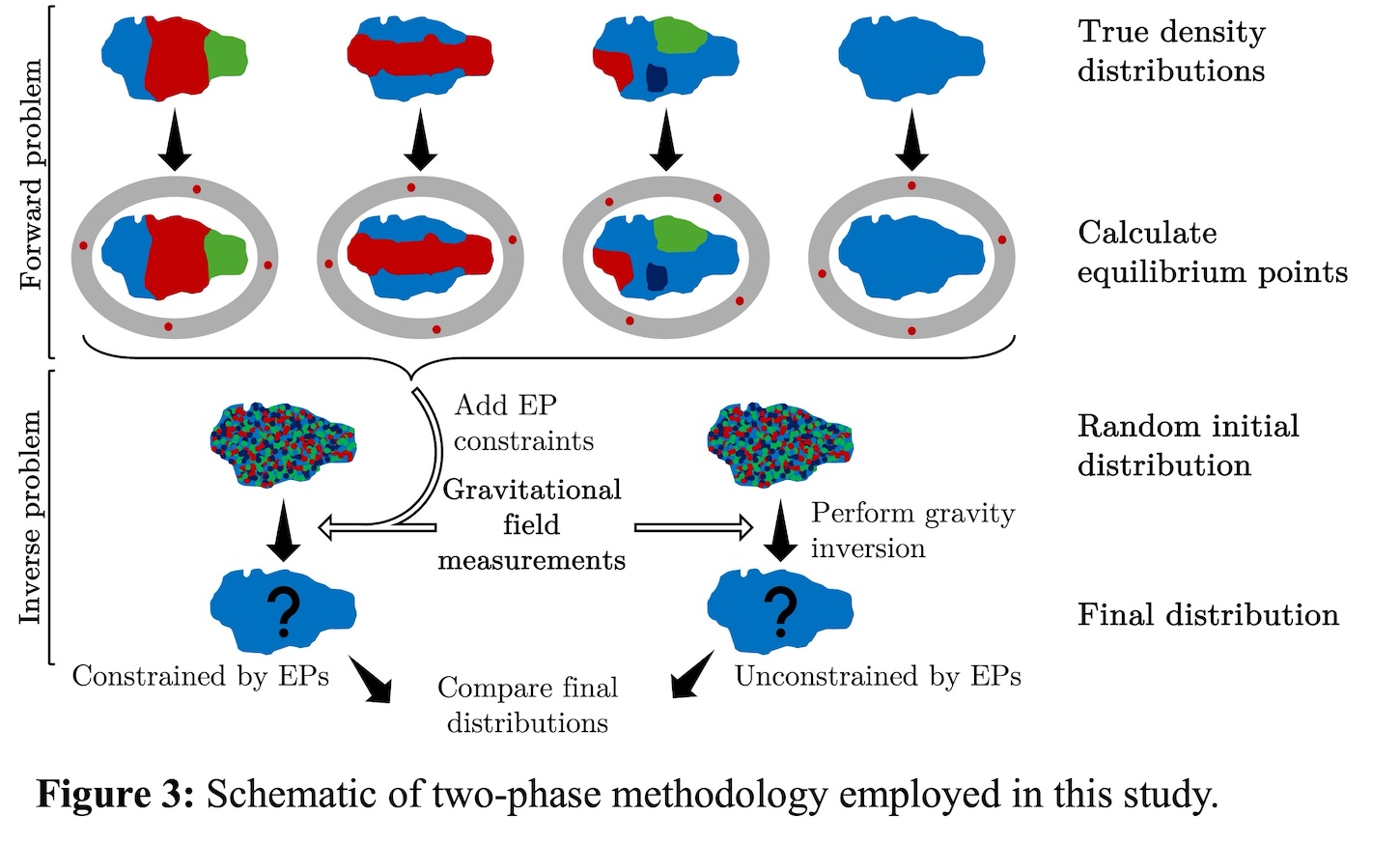
In summary, this work presents an analysis on the feasibility of using the location of equilibrium points around a small body to restrict the inverse gravity problem. By exploring how these locations respond to different mascon configurations and incorporating equilibrium point data alongside traditional gravitational measurements, it is investigated whether solution ambiguities could be reduced by these dynamical constraints.

 

Acknowledgments

Amelia Samuel was supported by ESA-OSIP Grant Number 4000142822/23/NL/MGu/nh

Dr Stefania Soldini was supported by the Medical Research Council UKRI-FLF grant number MR/W009498/1

Professor Monica D’Onofrio was partly funded by the European Union’s CHIST-ERA programme under grant agreement CHIST-ERA19-XAI-009 (MUCCA)

References

[1] B. A. Jones, “Efficient models for the evaluation and estimation of the gravity field,” Ph.D. dissertation, University of Colorado at Boulder, 2010.

[2] M. Kaasalainen, T. Kwiatkowski, M. Abe, et al., “CCD photometry and model of MUSES-C target (25143) 1998 SF36,” Astronomy & Astrophysics, vol. 405, no. 3, pp. L29–L32, 2003.

[3] S. J. Ostro, L. A. Benner, M. C. Nolan, et al., “Radar observations of asteroid 25143 Itokawa (1998 SF36),” Meteoritics & Planetary Science, vol. 39, no. 3, pp. 407–424, 2004.

[4] S. Lowry, P. Weissman, S. Duddy, et al., “The internal structure of asteroid (25143) Itokawa as revealed by detection of YORPspin-up,” Astronomy & Astrophysics, vol. 562, A48, 2014.

[5] D. Scheeres, A. French, P. Tricarico, et al., “Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu,”Science advances, vol. 6, no. 41, eabc3350, 2020.

[6] M. Kanamaru, S. Sasaki, and M. Wieczorek, “Density distribution of asteroid 25143 Itokawa based on smooth terrain shape,” Planetary and Space Science, vol. 174, pp. 32–42, 2019.

[7] S. Soldini, T. Saiki, H. Ikeda, K. Wada, M. Arakawa, and Y. Tsuda, “The effect of “MASCONS” sphere packing onto the dynamical environment around rubble-pile asteroids: Application to Ryugu,” in Europlanet Science Congress 2020 (EPSC2020), Online, 21 September–9 October 2020, Paper EPSC2020-808, 2020. doi:10.5194/epsc2020-808. [Online]. Available: https://doi.org/10.5194/epsc2020-808.