Summary: The comet Halley presents a very short Lyapunov time. It is of the order of just one orbital period. However, it does not show any strong chaotic radial characteristic in a timescale of tens of orbital periods. That can be interpreted as a confined chaotic motion. In the current work we use an approach of computing the maximum Lyapunov Characteristic Exponent (LCE) divided into two components: one taking into account just the radial contribution and other without considering the radial contribution. This approach has already been applied to asteroids and small satellites of Saturn, which were identified as having confined chaos dynamical feature, and had small eccentricity orbital (< 0.1). However, the Halley's orbit is highly eccentric (> 0.96), what makes the study a challenge. The results found in this work show that the radial contribution of the maximum LCE of Halley is not dominant. Nevertheless, the problem is more complicated. Close encounters with the planets, mainly Jupiter, play an important role on its chaotic behavior. A detailed analysis of this dynamics will be presented.
A traditional tool for detecting whether a dynamical system is chaotic or not is based on the exponential variation of trajectories in phase space. The Maximum Characteristic Lyapunov Exponent (LCE) calculates this exponential divergence with respect to an initial separation between the trajectories, i.e., it verifies the sensitivity to the initial conditions of the sound system (Benettin et al. 1980). The inverse of the maximum LCE results in the Lyapunov time. This quantity is a time scale required for a chaotic system to exhibit its chaotic behavior.
In orbital dynamics, there are cases in which bodies present a relatively short Lyapunov rhythm, but their orbits do not present significant radial variations. Even after the Lyapunov time has passed, the body is still confined to a well-defined region of space. This is called "confined chaos". Having a radial variation that is not very significant motivates us to seek to understand the radial behavior of the orbit by analyzing the maximum LCE. One idea is to rewrite the maximum LCE using the radial distance of the orbit, or radial contribution of the maximum LCE, and see how close it is to the "complete" maximum LCE. If the radial contribution is very close to the maximum LCE, we can conclude that the chaos of the orbit is expressed radially, that is, after the Lyapunov time, the behavior of the orbit will show significant radial variations. Otherwise, if the radial contribution is treated as irrelevant near the maximum LCE, we can conclude that the radial chaos is weak and, even after the Lyapunov time, the orbit will show a radial behavior of small variation. Adopting this strategy, Winter et al. (2010) developed an approach for the design of the radial component of the maximum LCE. This strategy considered the case of planar motion and was applied to the main belt asteroids and the shepherd satellites of the F ring (see Saturn, Prometheus and Pandora) (Winter et al, 2010). More recently, Pereira et al. (2024) generalized the strategy to the three-dimensional case and applied it to the case of Saturn's satellite Atlas.
The works found in the literature indicate that comet 1P/Halley has chaotic behavior, with some different results about its Lyapunov time. The smallest of them found so far was approximately 70 years by Muñoz-Gutiérrez, Reyes-Ruiz and Pichardo (2015). On the other hand, its orbital evolution for several hundred years does not show any strong radial irregularity, indicating a confined chaotic behavior. However, in the case of Halley, the orbital eccentricity is quite high (> 0.96) in comparison with that of the asteroids and small satellites of Saturn (< 0.1) studied previously.
Applying the approach described above, the results shown in Figure 1 indicate that the radial contribution of the maximum LCE of Halley is not dominant, but it is also not neglegible. The dynamical evolution of Halley is more complicated. Muñoz-Gutiérrez, Reyes-Ruiz and Pichardo (2015) and Boekholt et al. (2016) showed that Jupiter has strong influence on Halley’s chaotic motion. We also found that the close encounters with the planets, mainly Jupiter, play an important role on its chaotic behavior. A more detailed analysis of this dynamics will be presented.
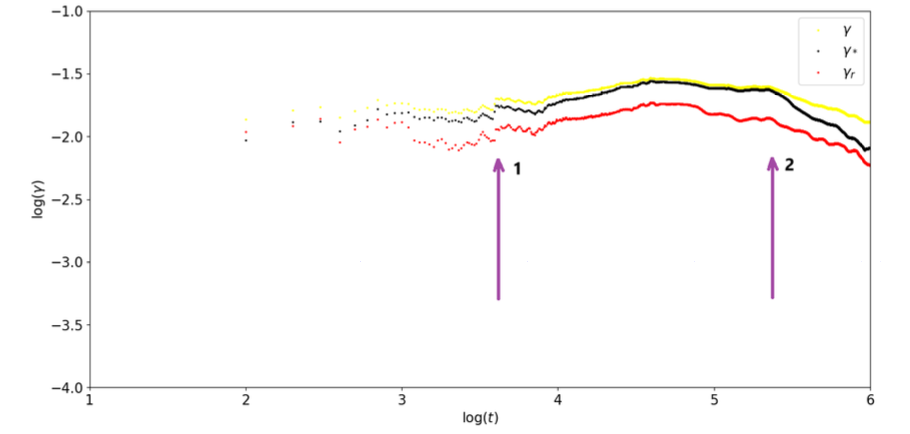
Figure 1. Lyapunov exponent for comet Halley. The yellow points represent Halley's maximum LCE, given by γ, the black points represent the LCE without taking into account the radial contribution (or remainder), given by γ∗, and the red points represent the radial contribution of the LCE, given by γr. The indications of numbers 1 and 2 correspond to close encounters with Jupiter.
Acknowledgements
This study was financed by CAPES – Finance Code 001, CNPq – Proc. 305210/2018-1, and FAPESP – Proc. 2016/24561-0.
References
Benettin, G. et al. Lyapunov Characteristic Exponents for smooth dynamical systems and for hamiltonian systems; a method for computing all of them. Part 1: Theory. Meccanica, 15, 9, 1980
Boekholt, T.C.N. et al. The origin of chaos in the orbit of comet 1P/Halley. MNRAS, 461, 4, 3576–3584, 2016.
Muñoz-Gutiérrez, M.A.; Reyes-Ruiz, M.; Pichardo, B. Chaotic dynamics of comet 1P/Halley: Lyapunov exponent and survival time expectancy. MNRAS, 447, 4, 3775–3784, 2015.
Pereira, L.S.; Mourão, D.C.; Winter, O.C. Confined Chaos and the chaotic angular motion of Atlas, a Saturn's inner satellite. MNRAS, 529, 1012-1018, 2024.
Winter, O.C; Mourão, D.C.; Giuliatti Winter, S.M. , Short Lyapunov time: a method for identifying confined chaos. A&A,523, A67, 2010.
