Constraining Martian Ice Deposits from an Effective Density Approach to Gravity and Topography and Implications for a future Mars Gravity Mission

Introduction: Gravity and topography are valuable tools for understanding climate records on Mars. Specifically, they help constrain the volume and composition of large ice masses including the Polar Layered Deposits (PLDs) and subsurface ice sheets in the mid-latitude regions. The South Polar Layered Deposits (SPLDs) in particular are known to reach up to ~3.7 km thick [1] and have a composition primarily of water-ice mixed with dust [e.g., 2]. Understanding vertical and lateral dust variations across the SPLD will advance our ability to understand how material is deposited and sublimated over time in response to an orbitally controlled climate. Mid-latitude ice deposits share similarities in composition [3] as well as implications for understanding Mars’ climate and habitability. They may also represent water resources for potential human exploration [4], such as the Arcadia plains and the glacial deposits of Deuteronilus Mensae [5]. However, debates regarding the spatial distribution, structure, thickness, and total volume of these deposits remain [e.g., 3,6].

Methods: We use localized effective density techniques. Although the analysis of ice deposits with gravity is challenging because of the current precision and resolution of the Martian gravity field (known to spherical harmonic degree and order 120 [7]), these techniques allow us to quantify bulk density at different spatial scales by comparing free-air gravity to the Bouguer correction (gravity predicted from topographic relief) [8]. Our work advances on that of [9] by using these techniques to specifically constrain ice deposits. For the SPLD, density variations can inform us on variations in dust content. For the mid-latitude deposits, we can either match the thickest ice deposits to other independent data sets (such as the ice consistency maps of [5]) or place upper limits on their thicknesses. In both settings, these techniques can help set measurement requirements for future gravity data to address scientific questions. We obtain localized effective density (ρ_eff) estimates by filtering the window of the gravity field in spherical harmonics with Slepian functions [e.g., 10], which define a spatial concentration from an angular size θ and a spectral concentration from a bandwidth L. Using the Python package SHTOOLS [11] and the methods described in [9], we compute localized ρ_eff spectra across the Martian surface at specified latitudes and longitudes.

Results: Mars’ gravity field has highest resolution at the south pole, allowing us to work with higher bandwidths and examine the SPLD regionally. The effective density of the south polar region of Mars is shown in Figure 1. We use L=20 and θ=10°, yielding a best-concentrated localization window with a concentration factor of 0.96. Between 90°S and 70°S, we calculate ρ_eff spectra at longitudinal increments of 2° and latitudinal increments of 1°. To mitigate noise in the gravity data, we take a flexible approach in interpreting different spherical harmonic degrees in different regions. Up to the maximum degree we can consider given the local degree strength and L, (typically between degrees 60<l<75), we select the ρ_eff value corresponding to the spherical harmonic degree with the highest correlation between free-air gravity and gravity-from-topography. We do not report ρ_eff in regions where the maximum correlation <0.5, as these areas probably produce unreliable density estimates due to low correlation. We additionally track the maximum correlation between 60<l<75 and the degree at which the highest correlation occurs, which are shown as polar projections in Figure 1.

In the region of the SPLD, we observe 650<ρ_eff<2600 kg/m³, encompassing a past bulk estimate of 1220 kg/m³ [2]. We can interpret lateral variations in ρ_eff as potential variations in dust content and compare to the density maps of [12,13]. Similar to [12], we find some of the lowest densities close to the south pole as well as lower densities at Ultima Lingula. Similar to [13], we observe low densities between longitudes 0°-180°E across Australe Lingula, Promethei Lingula, and Ultima Lingula. We observe a similar trend towards higher densities near Australe Scopuli, and especially high densities between longitudes 180°-225°E that can be interpreted as a very low-ice content region, subsurface mass anomalies, or noise in the gravity data.

Discussion and Future Work: Our initial results for the SPLD quantify possible lateral variations in dust content, which may reflect different climate records at different past times. Ongoing work involves applying the same effective density approach elsewhere on Mars, focusing on density variations at the upper mid-latitude regions and forward modeling the effective density spectra (similar to the approach of [14]) of ice deposits. Additionally, our modeling approach will be used to set upper limits on ice sheet thicknesses from the current gravity data and inform measurement requirements for testing ice and climate-related hypotheses with the acquisition of future gravity data at Mars [15], such as from the MaQuIs mission concept [16].

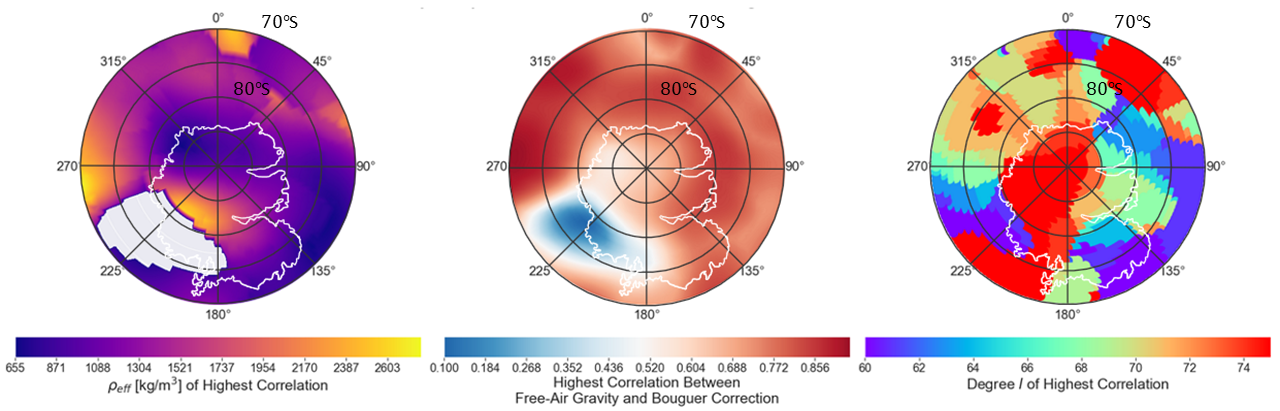
Figure 1: Maps of the south polar region, including effective density (left) corresponding to the highest correlation between 60<l<75, the values of those highest local correlations (middle), and the degree l at which the highest correlation occurs (right).

References: [1] Plaut, J., et al. (2007) Science, 316, 92-95. [2] Zuber, M., et al. (2007) Science, 317, 1718-1719. [3] Bramson, A., et al. (2015) GRL, 42, 6566-6574. [4] Dundas, C., et al. (2018) Science, 359, 199-201. [5] Morgan, G., et al. (2021) Nat. Astron., 5, 230-236. [6] Campbell, B., & Morgan, G. (2018) GRL, 45, 1759-1766. [7] Genova, A., et al. (2016) Icarus, 272, 228-245. [8] Besserer, J., et al. (2014) GRL, 41, 5771-5777. [9] Goossens, S., et al. (2017) GRL, 44, 7686-7694. [10] Wieczorek, M., and Simons, F. (2005) GJI, 162, 655-675. [11] Wieczorek, M. & Meschede, M. (2018) G3, 19, 2574-2592. [12] Li, J., et al. (2012) JGR: Planets, 117. [13] Genova, A., et al. (2024) Icarus, 414, 116025. [14] Izquierdo, K., et al. (2024) JGR: Planets, 129(2), e2023JE007867. [15] Sori, M., et al. (2024), 10th Int. Conf. on Mars, Abstract #3037. [16] Wörner, L., et al. (2023), Planet Space Sci., 239, 105800