Oral presentations and abstracts

The Earth is depleted in volatile elements relative to chondritic meteorites, its possible building blocks. Abundances of volatile elements descend roughly log-linearly with their calculated volatilities during solar nebula condensation [1, 2]. This depletion, however, is not accompanied by any stable isotope fractionation, which would otherwise be expected during vaporisation/condensation and atmospheric loss attending accretion [3, 4]. Thus, the physical processes that led to the formation of the Earth are yet to be reconciled with its chemical composition. Here, we integrate N-body simulations of planetary formation [5] within a framework that combines estimates for the compositions of planetary building blocks with volatile element losses during collisions, to link Earth’s elemental- and isotopic make-up with accretion mechanisms. The smooth pattern of volatile depletion in the Earth reflects the stochastic accretion of numerous, smaller, partially-vaporised precursor bodies whose elemental abundances are set by the heliocentric distances at which they formed. Impact events engender vaporisation, but atmospheric loss is only efficient during the early stages of accretion when volatile species can readily escape the gravitational pull of the proto-Earth. The chemical and isotopic compositions of the most volatile elements are controlled by that of late-accreting material, during which time the proto-Earth is sufficiently large so as to limit atmospheric loss. Stable isotopes of moderately- and highly volatile elements thus retain near-chondritic compositions.

[1] O’Neill and Palme (2008), Phil. Trans. R. Soc. 4205-38 [2] Braukmüller et al. (2019), Nat. Geosci., 564-9 [3] Wang and Jacobsen (2016), Nature, 521-4 [4] Sossi et al. 2018, Chem. Geol. 73-84 [5] Jacobson and Morbidelli (2014), Phil. Trans. R. Soc. 20130174

How to cite: Sossi, P., Stotz, I., Jacobson, S., Morbidelli, A., and O'Neill, H.: Stochastic accretion of the Earth, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-652, https://doi.org/10.5194/epsc2020-652, 2020.

Introduction:

Estimates of the bulk silicate Moon (BSM) composition have been proposed based on a number of different geochemical, petrological and geophysical arguments but have yet to arrive at a general consensus.
In order to obtain further constraints on the BSM composition, we investigated the effect of the BSM FeO content on the physical properties of lunar mantle reservoirs and tested the consistency of different lunar interior models with the bulk Moon density and moment of inertia.

Methods:

To cover all lunar interior models that are consistent with a given BSM composition, we modeled the properties of the chemical reservoirs forming from lunar magma ocean (LMO) solidification, considered the re-distribution of these reservoirs in the lunar mantle by solid state convection, and calculated the bulk Moon density and moment of inertia of the resulting interior models, assuming varying core properties and selenotherms.
Lunar Magma Ocean Crystallization:
We modeled LMO cumulate mineralogies using a combination [1] of crystallization algorithms from the software packages alphaMELTS [2] and SPICES [3], that has been validated against recent experiments on LMO fractional crystallization [4, 5]. Thereby we assumed pure fractional crystallization of a deep LMO, that extends to the core-mantle boundary so that the LMO comprises the whole BSM. The bulk LMO composition was chosen based on the estimate of [6]. FeO/MgO ratios of the bulk LMO composition were varied (8.0-13 wt% FeO) to investigate the effect of the FeO content on the densities and mineralogies of individual cumulate layers. All crystals forming in the LMO were assumed to sink and equilibrate with the liquid at the bottom of the magma ocean prior to fractionation, except for plagioclase which was assumed to float to the surface to form anorthositic crust. The average lunar crust thickness was assumed to be 40 km in accordance with recent GRAIL data [7]. Any excess plagioclase that formed after that final crust thickness was reached was assumed to remain in the mantle due to imperfect plagioclase floatation.
Mantle Mixing and Overturn:
As a consequence of the higher compatibility of lighter Mg compared to denser Fe in the LMO cumulate minerals, the density of the cumulate increases with progressing LMO solidification. Since the LMO solidifies from bottom to top, this results in a gravitationally unstable cumulate stratification that facilitates convective overturn, during which dense material sinks towards the core mantle boundary while lighter material migrates toward the surface. The respective changes in pressure and temperature experienced by individual cumulate layers, as well as mixing and chemical equilibration of different layers during overturn, can affect the mineralogy and physical properties of the lunar mantle. To investigate these effects, we calculated equilibrium mineral parageneses of different cumulate layers using Perple_X [8]. For simplicity we considered five homogeneous cumulate reservoirs (olivine-dominated, pyroxene-dominated, IBC, KREEP and crust), whose compositions were derived from the results of the LMO crystallization models by averaging the compositions of adjacent cumulate layers with similar mineralogies.
The mineralogies and densities of each reservoir were calculated as a function of depth along different selenotherms (e.g. [9]). To evaluate the effect of mixing and chemical equilibration, we also made the same calculations for different compositional mixtures of the layers.
The results of these calculations were used as input in a simple density structure model in order to investigate the effect of mantle overturn on the bulk lunar density and moment of inertia. Lunar core sizes and densities were thereby varied within the range of proposed values (e.g. [10]).

Results:

Changing the FeO/MgO ratio of the BSM composition leads to an earlier appearance and higher abundance of Fe-rich minerals in the LMO cumulate. This results in an increased thickness of the late formed, dense ilmenite bearing cumulate (IBC) reservoir, that we defined based on its high density compared to underlying cumulate layers. As a consequence, IBC thickness correlates linearly with the assumed LMO FeO content, varying by a factor of about 4 over the assumed range of FeO contents.
Due to its high density the radial distribution of IBC material in the lunar interior has a significant effect on the BSM moment of inertia, even though its volume is comparatively small. The effect of the distribution of IBC on the BSM moment of inertia increases systematically with increasing IBC volume, which is in turn linked to the FeO content.
Depending on the chosen core models and selenotherms, realistic bulk Moon densities and BSM moments of inertia could be reached assuming FeO contents of 8-13.5 wt%.

Discussion:

The range of possible FeO contents determined here is valid for a large variation of lunar interior properties and can be narrowed considerably by imposing constraints on the selenotherm, core properties or mantle structure. Seismic and selenodetic data indicate a mantle stratigraphy with a pyroxenitic upper mantle and a dunitic lower mantle [11] and suggest the presence of a dense, partially molten zone at the core mantle boundary [12], that might consist of sunken IBC material. These constraints on the interior structure of the lunar mantle indicate that BSM FeO contents of 9 – 11 wt% are most probable. This estimate could be further limited by tighter constraints on the size and density of the lunar core, e.g. by future seismic investigations.

References:
[1] Schwinger and Breuer (2018), AGU Fall Meeting, Washington, USA.
[2] Smith and Asimow (2005), G³, 6.2.
[3] Davenport (2013), Planet. Sci Res. Disc. Report 1, 173.
[4] Rapp and Draper (2018), Meteoritics & Planet. Sci. 53.7, 1432-1455.
[5] Charlier et al. (2018), Geochim. Cosmochim. Acta, 234, 50–69.
[6] O’Neill (1991), Geochim. Cosmochim. Acta, 55 (4), 1135-1157.
[7] Wieczorek et al. (2013) Science, 339, 671.
[8] Connolly (2005), EPSL, 236 (1-2), 524-541.
[9] Laneuville et al. (2013), JGR: Planets, 118 (7), 1435-1452.
[10] Weber et al. (2011), science, 331 (6015), 309-312.
[11] Gagnepain-Beyneix et al. (2006), Physics of the Earth and Planetary Interiors, 159 (3-4), 140-166.
[12] Matsumoto et al. (2015), GRL, 42 (18), 7351-7358.

How to cite: Schwinger, S. and Breuer, D.: Relationships between Bulk Silicate Moon FeO Content and Bulk Moon Physical Properties, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-739, https://doi.org/10.5194/epsc2020-739, 2020.

Overview. Terrestrial planets grew in a complex series of late stage giant impacts, and Moon-formation was among last to occur around Earth. But was it a singular event? Here we propose it was three or more episodes involving two bodies and the Sun, an almost-merger followed by an interlude, followed by a merger.

The standard model originated in the 1970s and has been surprisingly resilient [1]. It succeeds at making a Moon-size moon with Moon-like rocky and volatile-depleted composition, and sets the stage for the lunar magma ocean and tidal evolution. The model is only relevant to v_imp no faster than ~1.1 v_esc[2], which represents the median velocity of late-stage collisions [3,4]. Larger-velocity collisions encompass the other half of the probability distribution. At one end of the energetic spectrum, Theia could have originated from further out, as proposed by [5], but these collisions are dynamically disfavored [6].

To study giant impacts outside the limited realm of efficient mergers, our group has applied machine learning [7] and physical scaling [4] to hundreds of high resolution simulations over the expected velocities and impact angles and mass ratios. A definitive conclusion is that hit-and-run collisions (HRCs) are much more probable than mergers in the common velocity range v_imp ~1.1−1.4 v_esc. They spin up the target, strip mantle from the projectile [8], and send it back into space along with its remnants − but do not create the Moon (although see [9]). 

The solution we propose (Figure 1) is that Theia is the "runner" from a prior HRC with protoearth. The one-two blow leads to greater mixing and slows the bodies down by tens of percent so they will merge eventually. [10] found that many or even most late stage accretions are collision chains of varying complexity; on this basis we explore a three-act origin of the Moon: an HRC between prototheia and protoearth; a ~10³ to 10⁶ yr interlude featuring sweep-ups and close encounters; and a low-velocity merger resembling the standard model. 

The standard model is appealing for astrophysical and petrological reasons. It invokes what seems to be a typical "late stage" accretion of two terrestrial embryos, resulting in an Earth-Moon system of the right mass and angular momentum. And it predicts a volatile-depleted silicate Moon with a small iron core. Also, it is a near-perfect merger of the type that is implicitly assumed in N-body simulations. Under those assumptions runners cannot exist. 

To address the major deficiencies of the standard model while preserving its major strengths, we have developed a theoretical basis for a collision chain origin of the Moon. We show it to be a common pathway of planet formation, slowing the random velocities until merger is probable. There are innumerable pathways so it is premature to hone in on one scenario. A scenario meriting further research is an ~0.2 M_Earth planet that become a mantle-stripped Theia, that then returns thousands to millions of years later for a merger on a strongly unaligned impact axis.

Modeling. Act I assumes a non-rotating protoearth 0.9 M_Earth in circular orbit at 1 AU, of 30/70wt% iron/rock composition. Prototheia is 0.15 M_Earth with the same composition and entropy profile. We model representative HRCs with v_imp = 1.1 or 1.2 v_esc and impact angles θ_imp = 43° to 55°. These are selected so the runner ends up ~0.1 M_Earth to match the standard model. The target neither gains nor loses much mass, but it acquires a rotation period of 8 to 11 hours for these HRCs. No significant disk is produced. 

We calculate the egress velocity of the runner, which we then transfer into an N-body code [11] for Act II. To represent all possible collisions, we clone each SPH outcome into 1000 random orientations and evolve each clone, including the other major planets, until they have another collision with a planet, or for 50 Myr when most giant impact chains are finished. One set of outcomes is shown in Figure 2, where the HRC velocity v_imp/v_esc = 1.20 (red dashed line) gets slowed down to an egress velocity of 1.01 v_esc (black dashed line). Most clones return, tallied in Figure 2 by return velocity and interlude duration. Most return in ~10⁵ years at close to the egress velocity.

By design, Act III resembles the standard model, but with an extra stage of mixing that helps solve the lunar isotope problem and slows the bodies down so that merger is probable. We apply the same compositional and entropy profiles to the target, but give it more mass (0.95 M_Earth) and induce a rotation period of 8-12 hours per Act I. Theia, the runner, is now 0.1 M_Earth. Some of its mantle comes from protoearth, which would further reconcile the isotopic similarities. Altough every HRC is different, for simplicity we assume one 30/70wt% runner. We set the return velocity as either 1.00 or 1.05 v_esc and assume a nominal impact angle of 45°. Another variable is the offset angle between the two collisions, ranging from prograde (0°) to retrograde (180°), which would follow a random distribution [12]. The modeled return collisions are therefore variants of the standard model, and end up with a lunar mass or more in orbit in our simulations. 

References

[1] Hartmann, W.K. RSPTA, 372, 20130249 (2014)

[2] Canup, R.M., Asphaug, E. Nature, 412, 708 (2001)

[3] Chambers, J.E. Icarus, 224, 43 (2013)

[4] Gabriel, T.S.J et al. ApJ, 892, 40 (2020)

[5] Budde, G. et al. Nature Astronomy, 3, 736 (2019)

[6] Jackson, A.P. et al. MNRAS, 474, 2924 (2018)

[7] Cambioni, S. et al. ApJ, 875, 40 (2019)

[8] Asphaug, E. et al. Nature, 439, 155 (2006)

[9] Reufer A. et al. Icarus, 221, 296 (2012)

[10] Emsenhuber, A. et al. ApJ, 891, 6 (2020)

[11] Chambers, J.E. MNRAS, 304, 564 (1999)

[12] Emsenhuber, A. & Asphaug, E. ApJ, 875, 95 (2019)

How to cite: Asphaug, E., Emsenhuber, A., Cambioni, S., Gabriel, T. S. J., and Schwartz, S. R.: Moon Formation in Three Acts, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-485, https://doi.org/10.5194/epsc2020-485, 2020.

Intensive tidal heating makes the Galilean satellite Io to an outstanding example of a volcanically active world. Most of the heat generated in the interior is lost through a large number of active volcanoes. The distribution of Io's volcanoes on the surface could help us to constrain properties below Io’s crust, regulating the heat transport mechanism. For this study, we assume that (1) the presence of global volcanism is linked to the presence of melt in the upper mantle; that (2) the large-scale variation in volcanic density is inherited from non-uniform tidal heating and smoothed by vigorous convection; and that (3) the total number of hot-spots is controlled by the spatial frequency of thermal instabilities in the convecting layer. Three unknown parameters are explored: the fraction of convective heat transport compared to magmatic heat transport, the mantle viscosity, and the thickness of the heated layer. In order to evaluate which combinations of interior properties can explain Io's present volcanic distribution, we develop a model based on parameterised heat flow scalings to approximate different spatial characteristics of Io's interior convection pattern. Our model combines internal heating, and convective and magmatic heat flow. Parts of the parameter space that are not in agreement with the observation-derived conditions are ruled out.

Our results show that the observed small- and large-scale characteristics of Io's volcanic pattern can be explained by sub-lithospheric anomalies caused by convection. Solutions that allow for active volcanism and Io's specific large-scale variations in volcanic activity range from a thick mantle of high viscosity (10¹⁷ Pa s) to a thin asthenosphere of low viscosity (10¹² Pa s). If Io's volcanos are correlated to the spatial frequency of thermal instabilities, the range of Io's total volcanic features between 250 and 3030 can further constrain the parameter space. This favours a mantle with a low melt fraction, a low mantle viscosity, and a magmatic heat transport of >80%.

How to cite: Steinke, T., van Sliedregt, D., Vilella, K., van der Wal, W., and Vermeersen, B.: Constraints on Io’s interior by combining small- and large-scale characteristics of the volcanic pattern, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-859, https://doi.org/10.5194/epsc2020-859, 2020.

The volatility of an element is defined by its 50% condensation temperature (T_c⁵⁰) from a canonical nebular gas of Solar composition at 10^-4 bar [1, 2]. However, the variability in metallicity and metal/oxygen ratios of extrasolar systems inferred from the spectroscopic measurements of their parent stars [3, 4] implies that the identity, abundance and sequence of condensation may deviate from that of our solar system. As such, planets formed at similar heliocentric distances may be expected to have distinct compositions from those of the terrestrial planets in our solar system. Here we investigate the degree to which nebular composition influences the condensation process by taking nine sets of stellar compositions with variable metallicities that span the range from -0.4 to +0.4 dex and performing Gibbs free energy minimisation calculations with FactSage, including treatment of mineral solid-solutions,  over the temperature range 1723 K to 473 K.  We find that, although the general order of condensation is similar, absolute values of T_c⁵⁰ are shifted to higher temperatures at higher dex, where T_c⁵⁰(S), in particular, increases relative to those of other elements. Condensing nebulae with high metallicities (and also high metal/oxygen ratios) also exhibit the following features: (i) the appearance of reduced assemblages (e.g. CaS oldhamite, forsterite-rich olivine and graphite) in the condensates, (ii) increased fractions of oxygen (relative to its total abundance) locked in the silicate condensates, and (iii) lower fO₂ in the gas phase. As a result, these characteristics will lead to significant differences in the chemistry of planetary building blocks, which are then accreted to form telluric planetary bodies.

References

[1] Lodders 2003. ApJ 591:1220-1247. 

[2] Wood, B. J., Smythe, D. J., & Harrison, T. 2019. Ame. Miner. 104:844-856.

[3] Buder, S., Asplund, M., Duong, L. et al. 2018. MNRAS 478:4513:4552.

[4] Delgado Mena, E., Moya, A., Adibekyan, V., et al. 2019. A&A 624:A78.

How to cite: Wang, H., Sossi, P., and Quanz, S.: Nebular condensation of different stellar compositions and its influence on planetary chemistry, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-874, https://doi.org/10.5194/epsc2020-874, 2020.

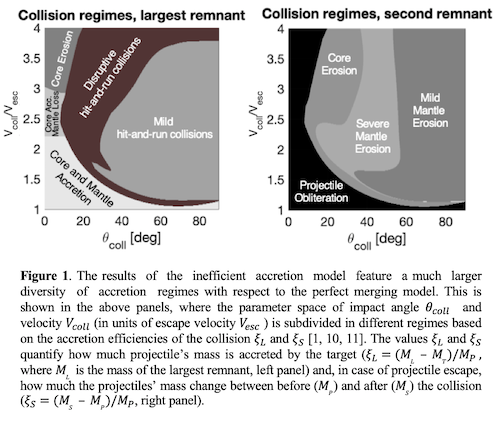
Summary: Inefficient accretion is a common outcome of planet-planet collisions which dominate the late stage of terrestrial planet formation [1]. These giants impacts create deep magma oceans on the resulting bodies [2], thus promoting multi-step core formation [3]. Here we present how planetary differentiation is affected by inefficient accretion and compare the results to those obtained assuming that collisions are perfectly accretionary (“perfect merging”). We find that the two models provide similar predictions for the mass and core mass fraction of planets more massive than 0.1 Earth’s masses (~1 Mars’ mass), in agreement with previous studies [4]. At smaller scales, however, the inefficient accretion model predicts a higher degree of planetary diversity in terms of core mass fraction. Smaller final planets, by definition, do not participate in many merging giant impacts but may participate in multiple hit and run collisions as either the target or the runner, both of which may leave a strong signal in a small planet's composition. Alternatively, due to the more extensive growth history of larger final planets, these regress to an average composition through the incorporation of many smaller embryos, effectively erasing gross signatures of hit and run collisions.

Why we need to model inefficient accretion: Planet formation models typically assume that, when a target of mass M_T accrete a projectile of mass M_P, the resulting planet has mass M_T + M_P (e.g., [5]). However, numerous studies show that the projectile often manages to escape accretion (hit-and-run collisions, [6]) and substantial debris can be produced (e.g., [7, 8, 9]). We capture this effect using machine learning [10, 11]. We train neural networks to predict the outcome of the collision (mass of the resulting bodies, their post-impact orbits and core-mass-fractions) from knowledge of the impact properties (target’s and projectile’s masses, and impact angle and velocity). The training, validation and testing set is a large but sparse collection of high-resolution Smoothed Particle Hydrodynamics simulations of giant impacts. We combine the neural networks with rigorous planetary differentiation models ([12, 4]) to study how the chemical equilibrium between the Si- and Fe-rich liquids (the planets’ mantle and the core, respectively) evolve as the pressure, temperature and oxygen fugacity of metal silicate equilibration change because of a giant impact. We assume that every collision is energetic enough to re-equilibrate the planets’ reservoirs. Future work will aim to relax this assumption.

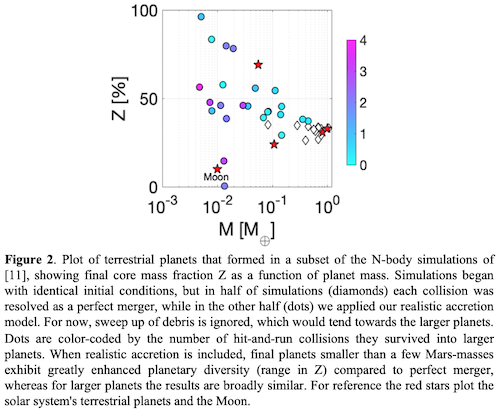
Inefficient accretion versus perfect merging: We first present a case study of a single collision solved using the inefficient accretion model trained on impact simulation data (Figure 1). Where the perfect accretion model would feature a single regime, i.e., the two bodies are assumed to merge in all scenarios, impact simulation results exhibit a richer range of potential outcomes as a function of expected pre-impact conditions. As terrestrial planets conclude their formation in a series of giant impacts [1], we also study the cumulative effect of such collision chains on the final planets' core mass fraction (Figure 2) using some of the results of the N-body planet formation studies in [11].  These simulations start with the same initial conditions, but in half of them collisions are resolved as perfect merging, while in the other half collisions are modelled using the neural networks. We find that the final planets’ core mass fractions predicted by the inefficient accretion model (dots) agree with those of the perfect merging model (diamonds) for planets’ masses larger than 0.1 Earth masses. This is consistent with previous studies that successfully reproduced Earth’s Bulk Silicate abundances using the results from N-body with perfect merging [4]. At smaller scale, however, the diversity in core mass fraction is enhanced in case inefficient accretion is included. The “degree” of diversity is higher for planets that survived a higher number of hit-and-run collisions, thus linking the collision history of planets to their core mass fractions.

Take home message: Our findings confirm that giant impacts are powerful drivers of planetary diversity, especially for planets less than a few tenths the mass of the largest, e.g. Mars-mass planets in our solar system. A realistic treatment of planetary collisions in terrestrial planet formation is necessary to accurately track compositional evolution.

References: [1] Asphaug, E. (2010). ChEG, 70, 199-219, 2010. [2] Tonks, W. B., & Melosh, H. J. (1993). JGR: Planets, 98(E3), 5319-5333. [3] Rubie, D. C., and S.A. Jacobson (2016). Deep Earth, 217:181-190. [4] Rubie, D. C. et al. (2016) Science 353.6304: 1141-1144. [5] Chambers (2001). Icarus, 152(2), 205-224, [6] Agnor, C., & Asphaug, E. (2004), ApJL, 613, L157. [7] Kokubo, E., & Genda, H. (2010), ApJL, 714, L21; [8] Stewart, S. T., & Leinhardt, Z. M. (2012), ApJ, 751, 32. [9] Burger, C et al. (2018), Celest. Mech. Dyn. Astron., 130, 2. [10] Cambioni, S., et al (2019). ApJ, 875, 40. [11] Emsenhuber, A. et al., (2020) ApJ, 891, 6.  [12] Rubie, D. C., et al. (2015). Icarus 248: 89-108.

How to cite: Cambioni, S., Jacobson, S. A., Emsenhuber, A., Asphaug, E., Rubie, D. C., Gabriel, T. S. J., Furfaro, R., and Schwartz, S. R.: The Effect of Inefficient Accretion on Planetary Differentiation, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-407, https://doi.org/10.5194/epsc2020-407, 2020.

Observations of Earth-sized exoplanets are mostly limited to information on their masses and radii. Simple mass-radius relationships have been developed for scaled-up versions of Earth or other planetary bodies such as Mercury and Ganymede, as well as for one-material spheres made of pure water(-ice), silicates, or iron. However, they do not allow a thorough investigation of composition influences and thermal state on a planet’s interior structure and properties.

As shown in Figure 1, we investigate the structure of a rocky planet shortly after formation and at later stages of thermal evolution assuming the planet is differentiated into a metal core and a rocky mantle (consisting of Earth-like minerals, but with a variable iron content).

Fig. 1: Temperature (left), pressure (centre), and density (right) profiles for two example planet masses of one and two Earth masses considering
the hot temperature scenario and assuming di erent planet iron contents. From Noack and Lasbleis, 2020.

We derived possible initial temperature profiles after the accretion and magma ocean solidification following Stixrude (2014). We then developed parameterisations for the thermodynamic properties inside the core depending on planet mass, composition, and thermal state. We provide the community with robust scaling laws for the interior structure, temperature profiles, and core- and mantle-averaged thermodynamic properties for planets composed of Earth’s main minerals but with variable compositions of iron and silicates, see Figure 2.

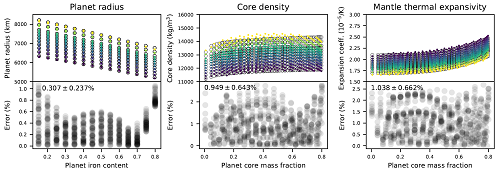
Fig. 2: Comparison between interior structure model data (filled circles) and predicted data from our parameterised model (black empty circles)
for different planet parameters and planet masses, with colours ranging from 0.8 (dark blue) to 2 (yellow) Earth masses. Grey circles show the
individual errors. The mean error with one standard deviation is listed for each error plot. From Noack and Lasbleis, 2020.

The interior structure profiles, an online tool and the link to the repository including all Python Jupyter notebooks, that were needed to derive the scaling laws and figures of this study, as well as an implementation of the scaling laws in Python are available on the following website: http://geodyn-chic.de/tools.

The scaling laws make it possible to investigate variations in thermodynamic properties for different interior thermal states in a multitude of applications such as deriving mass-radius scaling laws or estimating magnetic field evolution and core crystallisation for rocky exoplanets.

References

Stixrude, L. 2014, Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci., 372, 20130076

Noack, L. and Lasbleis, M. 2020, A&A, 638, A129

How to cite: Noack, L. and Lasbleis, M.: Parameterisations of interior properties of rocky planets, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-947, https://doi.org/10.5194/epsc2020-947, 2020.

Introduction

Present geochemical models of planetary core formation commonly focus on either element abundances or isotope fractionation between mantle and core. Data gathered from these two techniques can be mutually inconsistent, leading to different conclusions concerning core formation processes. An example of this is the Si content of the Earth’s core. Element partitioning data and seismological observations indicate that the Earth’s core only contains minor amounts of Si [1], whereas isotopic data suggests significant amounts of Si may be present [9]. 

To address this data discrepancy problem, this study combines element partitioning behaviour and isotope fractionation of Fe and Zn through metal-silicate partitioning experiments. Metal-silicate partitioning experiments at high pressure and temperature allow for the distribution of elements and their isotopes between planetary cores (metal) and mantles (silicate) to be studied under controlled conditions [e.g. 6,7, 10]. As during planetary core formation it is assumed that some form of equilibrium is reached over millions of years, the experiments should reflect this as well. Therefore, it is essential to determine the time that is required for every experiment to achieve both elemental and isotopic abundance equilibrium.

Approach

Metal-silicate partitioning experiments are performed under high pressure and temperature conditions using an end-loaded piston-cylinder press. To solely focus on the equilibration times, experiments of the same starting compositions were subjected to peak conditions of 1GPa and 1823K for a time ranging from 3 minutes up to 12 hours. The experiments consisted of a synthetic analogue of the lunar Apollo 15 Green Glass as silicate phase [3], along with a metal phase of Fe-metal doped with Zn.

Element concentrations of metal and silicate phases of every experiment were measured with an electron microprobe (EMPA) for major elements and laser ablation ICP-MS (LA-ICP-MS) for trace elements. To analyse Fe and Zn isotopic fractionation, both Zn and Fe were isolated from the metal- and silicate phases through ion-exchange chromatography. The AG-X8 resin was used for the separation of Fe, and the AG-MP-1 resin for Zn [5]. The isotopes of Fe and Zn were subsequently measured using a multi-collector ICP-MS (MC-ICP-MS) with a double spike technique. The precision of the isotope analyses is determined by measuring isotopic reference materials. The standards IRMM-014 (Fe) and ETH-ZN indicate a precision of ± 0.03‰ (2SD) for Fe isotopes and  ± 0.05‰ (2SD) for Zn isotopes respectively. Additionally, rock standards such as BHVO-2, BCR-2, AGV-2 and BIR-1 that had been processed exactly like the experiments were measured during the analyses.

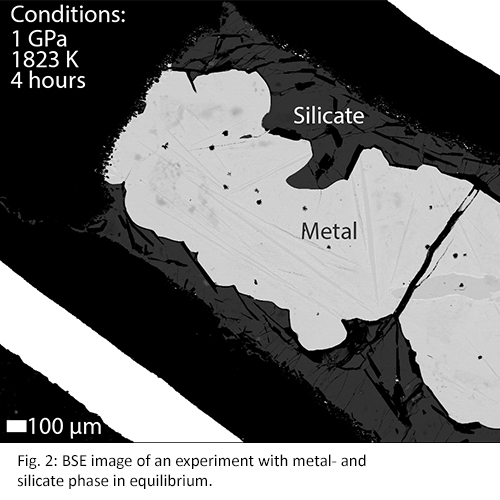
Results

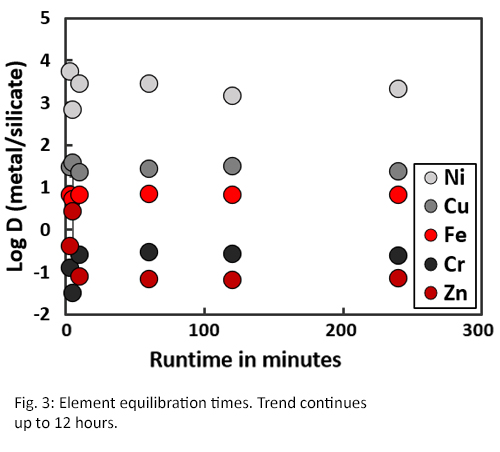
Experimental run products typically show a good separation of a metallic phase and quenched silicate melt. Disequilibrium within experiments can cause heterogeneous spots where groups of elements are clustered. These heterogeneous spots can be seen in experiments of run times of e.g. 3 and 5 minutes (Fig. 1), whereas they are absent in experiments with longer run times (Fig. 2). Results shown in Fig. 3 confirm these observations as the measured elements from short (<10 minutes) experiments show different partitioning behaviour compared to longer experiments (>30 minutes). Therefore, concentration analyses indicate that elemental equilibrium is reached within 30 minutes.

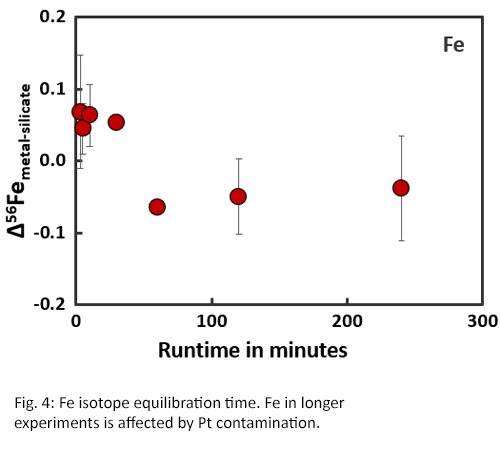
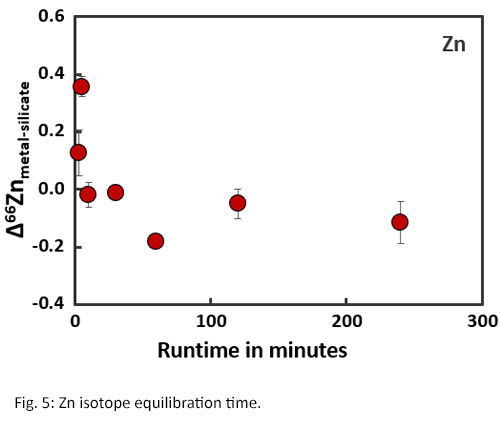
Isotope equilibration times are significantly longer than concentration equilibration times (Fig. 4 and 5) [8]. Within the first two hours of an experiment, the fractionation factors Δ⁵⁶Fe_{metal-silicate} and Δ⁶⁶Zn_{metal-silicate} are positive and variable. Between 2-4 hours, the fractionation factors become negative and start to stabilise. After approximately 4 hours, isotopic equilibrium is reached for both Fe and Zn with Δ⁵⁶Fe_{metal-silicate} = -0.04‰ ± 0.07 and Δ⁶⁶Zn_{metal-silicate} = -0.11‰ ± 0.06, which corresponds with literature data [2,4].

Discussion and outlook

Although the data described here cannot be directly applied to planetary core formation models yet, it is essential for creating models of core formation based on a combination of elemental abundances and stable isotope fractionation. This initial data set suggests that there is a relatively uniform Fe and Zn distribution between core (metal) and mantle (silicate) during core formation at high temperature. However, quantification of the effects of pressure, temperature and composition will be needed to further test this hypothesis.

Acknowledgements

We would like to thank the Netherlands Space Office for financial support through its User Support Programme.

References

[1] Badro, J., Côté, AS., and Brodholt, JP.: A seismologically consistent compositional model of Earth’s core, Proceedings of the National Academy of Sciences, 11, pp. 7542-7545, 2014.

[2] Bridgestock LJ., Williams H., et al.: Unlocking the zinc isotope systematics of iron meteorites, Earth and Planetary Science Letters, 400, pp. 153-164, 2014.

[3] Delano, JW.: Pristine lunar glasses : criteria, data and implications, Journal of Geophysical Research, 91, pp. 201-213, 1986.

[4] Hin RC., Schmidt MW., Bourdon B.: Experimental evidence for the absence of iron isotope fractionation between metal and silicate liquids at 1GPa and 1250-1300°C and its cosmochemical consequences, Geochimica et Cosmochimica Acta, 93, pp. 164-181, 2012.

[5] Moeller K., Schoenberg R., et al.: Calibration of the New Certified Reference Materials ERM-AE633 and ERM-AE647 for Copper and IRMM-3702 for Zinc Isotope Amount Ratio Determinations, Geostandards and Geoanalytical Research, 36, pp. 177-199, 2012.

[6] Righter, K .: Metal-silicate partitioning of siderophile elements and core formation in the early Earth, Annual Reviews of Earth and Planetary Sciences, 31, pp 135-174, 2002.

[7] Rose-Weston, L., Brenan, JM., Fei, Y., et al .: Effect of pressure, temperature and oxygen fugacity on metal-silicate partitioning of Te, Se and S: Implications for Earth differentiation, Geochimica et Cosmochimica Acta, 73, pp.4598-4615, 2009.

[8] Roskosz, M., Luais, B., Watson, HC., et al .: Experimental quantification of the fractionation of Fe isotopes during metal segregation from a silicate melt, Earth and Planetary Science Letters, 248, pp. 851-867, 2006.

[9] Shahar, A., Ziegler, K., Young, ED., et al .: Experimentally determined Si isotope fractionation between silicate and Fe metal and implications for Earth’s core formation, Earth and Planetary Science Letters, 288, pp. 228-234, 2009.

[10] Siebert, J., Corgne, A., Ryerson, FJ .: Systematics of metal-silicate partitioning for many siderophile elements applied to Earth’s core formation, Geochimica et Cosmochimica Acta, 75, pp. 1451-1489, 2011.

How to cite: Seegers, A., van Zuilen, K., Stelwagen, R., van Westrenen, W., and Vroon, P.: Equilibration time of Fe & Zn concentrations and isotopes in metal-silicate partitioning experiments, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-824, https://doi.org/10.5194/epsc2020-824, 2020.

Small planets (1-3.9 Rearth) constitute more than half of the inventory of the 4000-plus exoplanets discovered so far. Smaller planets are sufficiently dense to be rocky, but those with radii larger than 1.6 Rearth are thought to display in many cases hydrogen/helium gaseous envelopes up to 30% of the planetary mass. These low-mass planets are highly irradiated and the question of their origin, evolution, and possible links remains open. Here we show that close-in ocean planets affected by greenhouse effect display hydrospheres in supercritical state, which generate inflated atmospheres without invoking the presence of large hydrogen/helium gaseous envelopes. We present a new set of mass-radius relationships for ocean planets with different compositions and different equilibrium temperatures, which are found to be well adapted to low-density sub-Neptune planets. Our model suggests that super-Earths and water-rich sub-Neptunes could belong to the same family of planets, i.e. hydrogen/helium-free planets, with differences between their interiors simply resulting from the variation in the water content. 

How to cite: Mousis, O., Deleuil, M., Aguichine, A., Marcq, E., and Acuna Aguirre, L.: Are sub-Neptunes irradiated ocean planets?, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-624, https://doi.org/10.5194/epsc2020-624, 2020.

Volatile loss, Differentiation and Collisions: Key to the Composition of Rocky Exoplanets

Many of the key characteristics and geology of our planet Earth today were determined during the planet’s formation. What about rocky exoplanets? How does rocky planet formation determine the properties, composition, geology and ultimately, presence of life on rocky exoplanets? 

In this talk I will discuss projects that investigate the link between rocky planet formation and the composition of rocky exoplanets. This work utilises unique observations that provide us with the bulk composition of rocky exoplanetary material. These observations come from the old, faint remnants of stars like our Sun, known as white dwarfs. 

White dwarfs should have clean hydrogen or helium atmospheres. This means that planetary bodies as small as asteroids can show up in the white dwarf’s atmosphere. Metallic species such as Fe, Mg or Ca provide the bulk composition of the accreted body. Several thousand polluted white dwarfs are now known.

Models indicate that outer planetary systems, like our Solar System beyond Mars, should survive the star’s evolution to the white dwarf phase. Scattering is a common process, and any bodies that are scattered inwards, a bit like sun-grazing comets in our Solar System, would show up in the white dwarf atmosphere.

What determines the composition of the rocky exoplanetary bodies accreted by white dwarfs? 

Models presented in Harrison et al, 2018, 2020 (submitted) find that the abundances observed in the atmospheres of white dwarfs can be explained by three key processes, notably galactic chemical evolution, loss of volatiles (thermal processing) and large scale melting  which leads to the segregation of material between the core, mantle and crust. Galactic chemical evolution determines the initial composition of the planet forming material. Thermal processing determines the loss of volatiles, be that CO and other gases, water, or moderate volatile species such as Na. Collisions between planetary bodies that have differentiated to form a core can lead to fragments dominated by core-rich or mantle-rich material. 

Core-Mantle differentiation is a common process in exoplanetary systems

High abundances of siderophile (iron-loving) compared to lithophile (silicate loving) speeches in some polluted white dwarfs indicate that accretion of a planetary body composed primarily of material from a planetary core (or alternatively mantle). Harrison et al, 2020, based on data from Hollands et al, 2017, 2018, present several examples of systems with extreme abundances, core-rich, mantle-rich or crust-rich. 

Bonsor et al, 2020 concludes that most polluted white dwarfs (>60%) have accreted the fragment of a differentiated exoplanetesimal. 

Post-Nebula volatilisation in exoplanetary bodies

Mn and Na trace the loss of volatiles in planetary bodies. The difference in behaviour of Mn and Na under oxidising/reducing conditions makes them a strong indicator of the conditions prevalent when volatile loss occurred. Mn/Na for the Moon/Mars indicate post-Nebula volatile loss  (Siebert et al, 2018). Harrison et al, 2020, in prep, provides the first evidence of post-nebula volatilisation in exoplanetary bodies utilising the Mn/Na abundances of polluted white dwarfs. 

How to cite: Bonsor, A., Harrison, J., Shorttle, O., Carter, P., Kama, M., Hollands, M., Gaensicke, B., and Leinhardt, Z.: Volatile loss, Differentiation and Collisions: Key to the Composition of Rocky Exoplanets, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-387, https://doi.org/10.5194/epsc2020-387, 2020.

The earliest atmospheres of rocky planets originate from extensive volatile release during one or more magma ocean epochs that occur during primary and late-stage assembly of the planet (1). These epochs represent the most extreme cycling of volatiles between the interior and atmosphere in the history of a planet, and establish the initial distribution of the major volatile elements (C, H, N, O, S) between different chemical reservoirs that subsequently evolve via geological cycles. Crucially, the erosion or recycling of primary atmospheres bear upon the nature of the long-lived secondary atmospheres that will be probed with current and future observing facilities (2). Furthermore, the chemical speciation of the atmosphere arising from magma ocean processes can potentially be probed with present-day observations of tidally-locked rocky super-Earths (3). The speciation in turn strongly influences the climatic history of rocky planets, for instance the occurrence rate of planets that are locked in long-term runaway greenhouse states (4). We will present an integrated framework to model the build-up of the earliest atmospheres from magma ocean outgassing using a coupled model of mantle dynamics and atmospheric evolution. We consider the diversity of atmospheres that can arise for a range of initial planetary bulk compositions, and show how even small variations in volatile abundances can result in dramatically different atmospheric compositions and affect earliest mantle geochemistry and atmospheric speciation relevant for surficial prebiotic chemical environments (5). Only through the lense of coupled evolutionary models of terrestrial interiors and atmospheres can we begin to deconvolve the imprint of formation from that of evolution, with consequences for how we interpret the diversity revealed by astrophysical observables, and their relation to the earliest planetary conditions of our home world.

How to cite: Lichtenberg, T., Bower, D. J., Hammond, M., Boukrouche, R., Tsai, S.-M., Sanan, P., Sossi, P. A., and Pierrehumbert, R. T.: Atmospheric speciation of rocky planets from magma ocean outgassing, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-255, https://doi.org/10.5194/epsc2020-255, 2020.

How to cite: Carone, L., Barth, P., Barnes, R., Noack, L., and Henning, T.: Desiccation of the TRAPPIST-1 Planets During Their Magma Ocean Phase, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-45, https://doi.org/10.5194/epsc2020-45, 2020.

Overview

Tidal interaction plays a unique role in coupling the thermal, orbital, and rotational evolution of close-in moons and exoplanets. The reaction of a planetary body subjected to tidal loading is determined by its interior structure, rheological properties, and orbital parameters. The interior and orbital dynamics are, conversely, affected by the tidal dissipation. In this study, we address the parameter dependence of stable spin states and tidal heating, as well as the long-term coupled thermal-orbital evolution of rocky exoplanets. Special attention is paid to the consistent evolution of spin rate and to the role of an emerging subsurface magma ocean in the secular maintenance of nonzero orbital eccentricity.

Model and Methods

Our model consists of several modules and relies on the semi-analytical description of the thermal and orbital dynamics. All processes are interconnected through the tidal dissipation, which drains the energy from the orbit and presents an additional heat source for the planetary interior. The tidal heat rate (e.g., Segatz 1988; Efroimsky and Makarov, 2014) as well as the evolution equations for the orbital parameters and the spin rate are calculated using the Darwin-Kaula expansion into modes corresponding to different tidal frequencies (Kaula, 1964). To quantify the deformation and the additional potential of the deformed planet, we calculate the complex tidal Love numbers k₂^*(ω) (e.g., Castillo-Rogez et al., 2011) using the equations of the normal mode theory (e.g., Sabadini and Vermeersen, 2004). This approach permits us to account for a differentiated interior of the planet.

The thermal evolution of the model planets is described by a parametrized model of stagnant lid convection (e.g., Grott and Breuer, 2008) with basal and volumetric heating, where the major heat source is provided by the tidal dissipation.  The internal dynamics are coupled to the rest of the model through the temperature dependence of mantle viscosity, the evolution of the stagnant lid thickness and the emergence of a stable subsurface magma ocean. All changes in the interior structure and rheological properties are reflected by the tidal Love number, which determines the tidal response and the rate of energy dissipation.

Results

The first goal of this study is to explore the parametric dependence of the tidal dissipation and the spin-orbit locking. We study the effect of different rheological parameters, the planet size, the interior structure, and the eccentricity. As a result of the viscoelastic rheology, the model planet can get locked into higher than synchronous spin-orbit resonances, which provide an important source of dissipation especially in the case of relatively low orbital eccentricities. We also find that planets with smaller radii are more likely to get locked into higher resonances than larger or more massive planets. In addition to a parametric study of a generic terrestrial exoplanet, we also apply the model on three currently known low-mass exoplanet candidates: Proxima Centauri b, GJ 411 b, and GJ 625 b.

The second goal is the assessment of the mutual interconnection between the secular thermal and orbital evolution. We investigate the evolution paths of the three mentioned exoplanets and observe that the thermal evolution proceeds as a sequence of thermal equilibria. The equilibrium temperature profiles of the tidally evolving exoplanets are governed primarily by the stable spin-orbit ratio, which is determined by the mantle viscosity and eccentricity. The temperature-driven changes in the interior and the transitions between different spin-orbit resonances also affect the rate of orbital evolution. Specifically, the final despinning of a planet to the synchronous rotation may slow down the circularization of the planetary orbit and help to maintain nonzero orbital eccentricity for a considerable time. Using the coupled model, we also study the effect of different initial eccentricities and mantle viscosities on the current thermal and rotational state of the three exoplanets and compare the resulting eccentricities with their current, empirically given values (Figure 1).

Figure 1: Orbital and thermal characteristics of Proxima Centauri b after 5 Gyr of coupled thermal-orbital evolution; adapted from Walterova and Behounkova (2020). Depending on the initial orbital eccentricity (x-axis) and the reference viscosity at temperature T₀=1600 K (y-axis), the individual panels depict the evolved eccentricity (left), the spin-orbit ratio (middle) and the surface tidal heat flux (right). Light blue areas correspond to the model parameters for which the evolved eccentricity complies with observation (Jenkins et al., 2019). The range of the empirically given values is also indicated by a red line in the first colorbar.

Conclusion

The orbital evolution of strongly tidally loaded exoplanets, whose thermal state is shaped by the tidal heating, is naturally interconnected with their internal dynamics. The changes in the interior, namely the partial melting and the formation of a subsurface magma ocean, translate into the decrease in the rate of orbital evolution and in the tidal heat generation. The understanding of this complex feedback may help us to better constrain the conditions on extrasolar worlds and to address their hypothetical habitability.

Acknowledgements

The research leading to these results received funding from the Czech Science Foundation through project No. 19-10809S and from Charles University through project SVV 115-09/260581.

References

[1] M. Segatz, T. Spohn, M. N. Ross, and G. Schubert. Icarus, 75(2):187–206,1988.

[2] M. Efroimsky and V. V. Makarov. The Astrophysical Journal, 795(1):19, 2014.

[3] W. M. Kaula. Reviews of Geophysics, 2(4):661–685, 1964.

[4] J. C. Castillo-Rogez, M. Efroimsky, and V. Lainey. Journal of Geophysical Research, 116(E09008), 2011.

[5] R. Sabadini and B. Vermeersen. Global Dynamics of the Earth: Applications of Normal Mode Relaxation Theory to Solid-Earth Geophysics. Kluwer Academic Publishers, Dordrecht, the Netherlands, 2004.

[6] M. Grott and D. Breuer. Icarus, 193(2):503–515, 2008.

[7] M. Walterova and M. Behounkova. Submitted to The Astrophysical Journal.

[8] J. S. Jenkins, J. Harrington, R. C. Challener, et al. Monthly Notices of the Royal Astronomical Society, 487(1):268–274, 2019.

How to cite: Walterova, M. and Behounkova, M.: The long-term tidal dynamics of differentiated rocky exoplanets, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-86, https://doi.org/10.5194/epsc2020-86, 2020.

Abstract
Ultra-short period planets (USP) that are rocky in nature are plentiful in the exoplanet catalogue and may host tectonic regimes without analogues in the Solar System. Recently, the transit phase-curve of the super-Earth LHS 3844b (radius = 1.303 Earth radii) has been mapped by a 100 h Spitzer observing campaign and is consistent with a bare-rock model of a tidally-locked planet [3].  We use phase map estimates of the planet's surface temperature distribution to infer the interior dynamics of LHS 3844b using a simulation of interior flow.  We infer that the strong dichotomy of surface temperature may lead to a dichotomy of interior dynamics, with implications for the interior-atmosphere exchange of volatiles in USP rocky planets.  We use a mantle convection code with parameters from the literature suitable for LHS 3844b.  The material properties of the interior, including viscosity, are constrained from previous theoretical calculations and laboratory experiments.

For models with a weak near-surface layer (lithosphere), hot upwellings are evenly distributed between the dayside and nightside, albeit strong cold downwellings form dominantly on the nightside. Upwellings on the nightside have less lateral mobility than the dayside because they are confined by downwellings.  In contrast, for models with a strong near-surface layer (lithosphere), the interior dynamics are mostly driven by a prominent downwelling on the dayside which flushes hot material from the lower thermal boundary layer around the core towards the nightside where upwellings preferentially arise.  Therefore, current and near-future space missions could detect a signal from volatile outgassing or volcanism driven by interior upwellings that is either globally uniform or originating from the nightside only.  A spatially-variable release of volatiles may produce corresponding asymmetries in astrophysical observations, such as secondary features in phase curves.

1. Methods
The geodynamic model is devised assuming an Earth-like composition with Perovskite (Pv) dominating the uppermost mantle and post-Perovskite (pPv) the lowermost mantle. A temperature- and pressure-dependent Arrhenius-type viscosity law is used with the lower-bound post-Perovskite parameters given in [2]. Mantle convection is modelled using the code StagYY [3] in a two-dimensional spherical annulus geometry. The effects of compressibility are modelled by employing the truncated anelastic liquid approximation (TALA) where a reference state density profile is assumed.
We include plastic yielding to model the brittle nature of the lithosphere. Yielding occurs when the local stress state exceeds a prescribed yield stress criteria, thereby modelling plate-tectonic-like behaviour at the surface. 

2. Results and Discussion
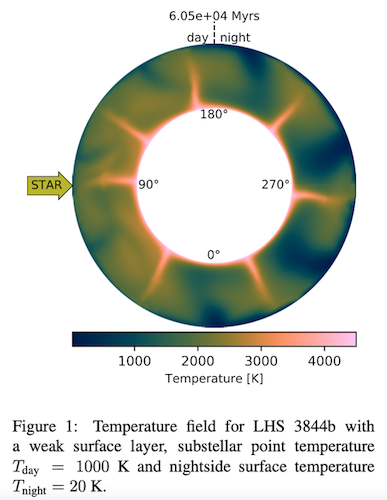
For models with a weak near-surface layer (low yield stress criteria), we find that hot upwellings are evenly distributed around the CMB. Downwellings form on both sides, but they are stronger on the nightside (Figure 1). The high viscosity upwellings tend to dictate the long-wavelength pattern of flow, and therefore shepherd the upwellings along the CMB into position between the downwellings. On the dayside, the upwellings exhibit more lateral motion as the downwellings are less viscous and thus the shepherding effect is less pronounced. 
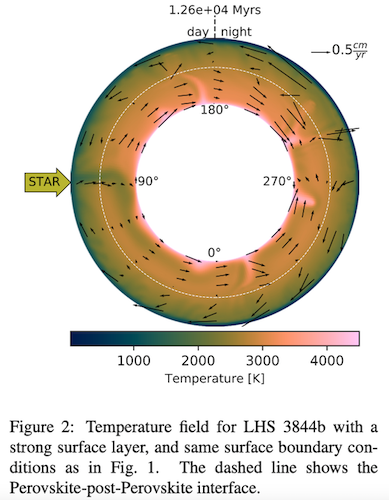
For a strong near-surface layer (large yield stress), an approximate degree-1 convection pattern is established: a prominent downwelling forms on the dayside and descends into the deep mantle. It flushes hot material from the lower thermal boundary layer around the CMB from the dayside to the nightside, thereby promoting the formation of upwellings on the nightside which rise to the surface. A return flow of cold material from the nightside to the dayside is established in the uppermost Perovskite layer (Figure 2).
An explanation for this flow pattern is that yielding does not occur on the nightside and therefore the formation of downwellings is inhibited. On the dayside, high temperatures weaken the near-surface through the strong temperature dependance of viscosity and therefore enable downwellings to form.

Previous work studying the interior dynamics of incompressible Earth-sized planets with asymmetric surface temperatures finds a flow pattern that is characterised by an upwelling near the substellar point and a near-surface flow from the dayside to the nightside [4]. Although this is also a degree-1 flow, it is reversed compared to our models. We surmise that the difference in flow direction is due to the strongly varying viscosity that we impose, and possibly the effects of compressibility and planet size.

In summary, our models show that a strong dichotomy of the surface temperature can lead to an asymmetry in the distribution of upwellings and downwellings in the interior of rocky super-Earths, depending on the strength of the near-surface layer.
An asymmetric flow pattern has not been inferred for any of the rocky Solar System planets, and therefore our work presents the first observation-constrained inference of a novel tectonic mode that is applicable to some rocky exoplanets.  In this regime, upwellings could produce corresponding asymmetry in the production of near-surface melt and subsequent outgassing, which can serve as a future test to distinguish between different model predictions.

Acknowledgements
TGM and DJB acknowledge Swiss National Science Foundation (SNSF) Ambizione Grant 173992.

References
[1] Tackley, Paul J.: Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the Yin-Yang grid, Physics of the Earth and Planetary Interiors, Vol. 171, pp. 7-18, 2008.

[2] Tackley, Paul J., et al.: Mantle dynamics in super-Earths: Post-perovskite rheology and self-regulation of viscosity, Vol. 225, pp. 50-61, 2013.

[3] Kreidberg, L., et al.: Absence of a thick atmosphere on the terrestrial exoplanet LHS 3844b, Vol. 573, pp. 87-90, 2019.

[4] Van Summeren, J., Conrad, C. P. and Gaidos, E.: Mantle convection, plate tectonics, and volcanism on hot exo-earths, Vol. 736, pp. 2-7, 2011.

How to cite: Meier, T. G., Bower, D. J., Lichtenberg, T., and Tackley, P. J.: Interior dynamics of tidally locked super-Earths: The case of LHS 3844b, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-778, https://doi.org/10.5194/epsc2020-778, 2020.

Melting processes inside the mantle of terrestrial planets are highly dependent on the planet’s heat budget and trigger the redistribution of incompatible trace elements from solid mantle rocks into the melt. Due to density contrasts, convective mantle motion, and other physical factors, this melt ascents towards the surface and takes most of these incompatible elements with it. Some of these ascending elements like ⁴⁰K, ²³²Th, and ²³⁸U, are radioactive and are important contributors to the Earth’s or other terrestrial planet’s heat budget. By redistributing these elements, the mantle is left depleted and the surface enriched, leading to a shift in the production of heat from the mantle towards the crust.

To be able to calculate the amount of redistributed heat producing elements, we model partition coefficients after Blundy and Wood 2003 [1] depending on temperature, pressure, and melt composition and trace them in a global convection code (Fig.1). For the incorporation of the elements’ partitioning behavior at higher upper mantle pressures, we took the thermodynamic approach from Blundy et al. 1995 [2] and parameterized it to higher pressures (Fig.2). The redistribution of heat producing elements between the mantle and crust has important implications for the cooling behavior of the interior. In turn, the latter affects the generation of melt in the mantle and the formation of crust.

[1] Blundy, J.D. and Wood, B.J. (2003), RiMG, 52 (1), 59–123.
[2] Blundy, J.D., Falloon, T.J., Wood, B.J., and Dalton, J.A. (1995), J. Geophys. Res., 100, 15501-15515.

Fig. 1: Redistributed amount of the heat sources ⁴⁰K, ²³²Th, and ²³⁸U on Mars after 600 Myrs.

Fig. 2: The clinopyroxene/melt partition coefficient of Na parameterized to higher pressures. With increasing pressures, partition coefficients increase. At the turning point, the model ceases to work. The applicability of the approach could be increased from 0-4 GPa to ≤12 GPa.

How to cite: Schmidt, J. M. and Noack, L.: Mantle evolution in terrestrial planets - Partitioning behavior of heat producing elements, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-966, https://doi.org/10.5194/epsc2020-966, 2020.

Besides the accretion from the solar nebular and the degassing from magma oceans, the main source of the atmospheres of terrestrial planets is magmatic volatile release from the interior. The atmosphere on early Earth is crucial for the emergence and evolution of life. It´s build-up and composition is largely influenced by magmatic outgassing. This outgassing process includes the well-studied extrusive as well as the often neglected intrusive volatile release. However, it is assumed that the intrusive magma production rates - at least on Earth - are significantly higher compared to extrusive rates, which makes the investigation and quantification of possible volatile exsolution processes even more important.

We simulate the crystallization of an intrusive magma body emplaced at different depths within the lithosphere. As the solubility of volatiles like H₂O and CO₂ increases with pressure, they usually do not exsolve from the melt. However, through the precipitation of nominally dry minerals, the remaining melt is enriched in incompatible elements and volatiles. They accumulate until a saturation level is reached and the volatiles exsolve. The composition of the resulting volatile phase depends on the solubility of the volatile species, the pressure and temperature, the initial composition of the melt, the partition coefficient and the oxygen fugacity. We consider these parameters in our model and benchmark our results with literature values. Additionally, we investigate the likelihood of reactions with the surrounding mantle, to form water-bearing minerals, during the ascent of volatiles. Finally, we quantify the impact of intrusive degassing on the build-up and composition of the atmosphere.

How to cite: Vulpius, S., Noack, L., Sohl, F., Ortenzi, G., and Hoffmann, E. J.: Volatile release from intrusive magma bodies of terrestrial planets, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-959, https://doi.org/10.5194/epsc2020-959, 2020.

Most planets located within the solar system display evidence of past and/or current magnetic activity. Magnetic fields of rocky bodies are thought to be driven by thermo-chemical convection taking place in an electrically conducting fluid in their deep interior (the liquid outer core for Earth), and are thus evidence of strong internal dynamics. Furthermore, magnetism is thought to play a crucial role for the development and the long-term stability of habitable surface conditions, as it shields the upper atmosphere from mass loss induced by stellar winds and extreme space weather events. 

The discovery of a large number of rocky exoplanets motivates the search and the study of magnetic fields beyond the solar system. While current observations are limited to providing the planetary radius and minimum mass, future missions aimed at the exploration of exoplanetary atmospheres will open up new avenues for the inversion of interior properties starting from atmospheric parameters. Such a goal requires knowledge of the planetary cores and the development of exoplanetary magnetic fields, as well as their influence on atmospheric evolution and its interaction with the surrounding stellar wind. 

The aim of the current study is to identify trends and parameter(s) controlling the core evolution and magnetic field sustainment in super-Earths. To do this we investigate the evolution of the cores of planets having different masses (0.8-2 Earth masses) and iron inventories (bulk iron content and mantle iron number). Starting out from the internal temperature profile after the complete solidification of a global magma ocean (Noack and Lasbleis, 2020), we determine the size and the structure of the core, and model its thermal and magnetic evolution during the subsequent 5 billion years. By taking into account the energy release resulting from the growth of a solid inner core, we compute the thermal and compositional buoyancy fluxes, as well as the generated magnetic field strengths and lifetimes. 

Our findings show that while the planetary mass is not a controlling parameter, both the bulk iron content and the mantle iron number strongly influence inner core growth and the lifetime of the magnetic field. Iron-rich planets having a high mantle iron number tend to start out and end up with solid inner cores that are substantially larger than iron-poor bodies, sometimes even reaching up to the radius of the outer core and thus shutting down magnetic activity. We therefore find that there is a “sweet spot” for longer-lasting magnetic fields, located at intermediate bulk iron contents and low mantle iron numbers.  

We also varied the content of light elements in the core and found that the addition of a small fraction of light elements helps keeping the magnetic field active for longer, even at high bulk iron contents. Field strengths can reach up to several times the one of Earth, even though such a signal might still be too weak to be detected by current radio telescopes. Nevertheless, the development of new observation techniques and the multiple future missions devoted to atmospheric exploration will provide useful insights on the presence and frequency of planetary magnetic fields.

How to cite: Bonati, I., Lasbleis, M., and Noack, L.: Exoplanetary magnetic fields as a tool for future interior characterization , Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1092, https://doi.org/10.5194/epsc2020-1092, 2020.