Poster presentations and abstracts

The JUpiter ICy moons Explorer (JUICE) (ESA) and Europa Clipper (NASA) missions will be launched in the next decade in order to spend a number of years making detailed observations of the giant gaseous planet Jupiter and three of its largest moons, Ganymede, Callisto, and Europa.

The focus of both missions is to scrutinize the nature of these icy moons and characterize the conditions that may have led to the emergence of habitable environment for life. A particular aspect of both JUICE and Europa Clipper missions is the exploration of the icy crusts, which comprises a new and very focused objective for outer solar system missions. A good example however of such investigations has been presented by Cassini’s RADAR instrument. One of JUICE’s tasks is to characterize the structure and properties of the ice shell by probing the subsurface of Ganymede down to a depth of a few kilometers. An additional task of JUICE’s ice penetrating RIME and Clipper’s radar REASON is to obtain profiles of subsurface thermal, compositional, and structural horizons down to a maximum depth of 1 to 9 km depending on the crust’s properties. However, the interpretation of radar sounding experiments relies on the ability to decipher the backscattering patterns.

The icy moons of Jupiter have been reported to be efficient backscatters of cm-wavelength radiations, showing polarization effects that must be due to factors other than the only single scattering process at the space-body surface interface. The identification of the characteristics of the backscattering radiation results from the superposition of backscattering layers with different electrical properties as a function of depth. Amongst the properties likely to modify the backscattering efficiency are: the amount of silicate (partial absorbers), the ice salinity, and the distribution of cracks present in the layer (inhomogeneity of the medium at size scales comparable to the radar wavelengths). Consequently, direct measurements of the dielectric values (electrical conductivity and permittivity) of an icy layer with properties controlled in the lab could unveil the backscattering efficiency of the sample.

We provide here the first version of a database of measurements, following a number of laboratory experiments made at CAB-CSIC-INTA, in collaboration with UCM and CSIC-ITEFI (Please see abstracts EPSC Muñoz-Iglesias et al. and EPSC Gonzalez-Díaz et al.), collected and classified based on the parameters and properties of the different ice samples, which are manufactured to resemble the Jovian moon ice compositions. During the experiments, different conditions of T and P were applied and the recorded measurements of electrical properties were collected in this database of ‘ice behavior’.

Since the next remote sensing data are not expected anytime before the arrival of JUICE and Europa Clipper (around 2030), the database provides us with the opportunity to compare with the current literature and the data available for the Jovian icy moons from previous missions, but also add information that is currently missing and relate that information to relative surface processes. The ice database would facilitate the interpretation of future radar sounding measurements, providing a better constrain on the true nature of ices of the surfaces of JUICE’s and Europa Clipper’s future targets.

How to cite: Solomonidou, A., Lorente, R., Muñoz Caro, G. M., Vallat, C., Altobelli, N., Witasse, O., Coustenis, A., Lopes, R., Le Gall, A., Elachi, C., Prieto-Ballesteros, O., Muñoz-Iglesias, V., and González Díaz, C.: Measurements of dielectric properties of ices in support to future radar measurements of Jovian Icy moons , Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-11, https://doi.org/10.5194/epsc2020-11, 2020.

Introduction

Enceladus is, arguably, one of the locations in the Solar System where we might expect to find life, or an indication of complex pre-biotic molecules: it has a sub-surface ocean which is spewing molecules into space which could be captured and analysed using in situ techniques such as the Enceladus Organic Analyzer [1] on-board either a fly-by or (preferably) orbiter mission. In preparation for such a mission the authors in [2] fired micron-sized PMMA particles (as ice analogues) at speeds of 1 – 3 km s^-1 into a range of metal targets to try and identify which material would be best suited as a capture surface. The conclusion was that indium (from a selection of gold, silver, copper and aluminium) was the best capture medium as it retained the greatest unmodified percentage of the original PMMA particles.

The next step in the project is to simulate these impacts so that parameters such as peak pressure and temperatures can be modelled to determine any potential modification to the impacting organic molecules. Once successful, this model can then be used for the simulation of icy impactors.

Modelling PMMA impacts into In.

Indium is a very soft (at room temperature), fairly inert material and could easily be space-qualified for a potential capture surface. Lots of data exist on the low strain-rate strength of indium (i.e. its creep strength) but at the impact speeds likely to be encountered at Enceladus (0.1 – 2 km s^-1) and the size of the impacting particles (~6 μm), the strain-rate, , expected is ~v/d ~ 10⁸ s^-1. At such strain-rates the strength of a material can be more than an order of magnitude higher than its quasi-static strength [3, 4]. Unfortunately, no data could be found for the high strain-rate strength dependence of indium. We therefore follow the approach taken successfully in modelling similar impacts into aluminium, tantalum and copper [5, 6] and assume that the strain-rate behaviour of indium follows a similar pattern (which is probably a justifiable assumption given that indium behaves as a FCC material).

From the results in [2] (replotted in Fig. 1) the crater diameter for PMMA impacts into indium is seen to be a non-linear function of the particle size and impact velocity, thus indicating a strain-rate strength dependence.

A further interesting observation from [2] was that the capture efficiency (i.e. the amount of the projectile retained in the crater) peaked at approx. 1 km s^-1 for indium, but decreased for lower velocities. This decrease occurs as the PMMA projectiles bounced off the target’s surface, leaving a dent but very little detectable residue, and this behaviour is replicated in the modelling using the strength models described here for PMMA and indium.

A modified Cowper-Symonds strength model [5, 6, 7] was used for both PMMA and indium. The Cowper-Symonds model has a strain-rate strength dependence which scales as the power of the strain-rate, unlike similar constitutive models (i.e. Johnson-Cook) where the strain-rate strength dependence is logarithmic.

To account for melting of the target material we used a modified version of the Cowper-Symonds equation (written as a user sub-routine in AUTODYN) which also incorporates a thermal softening term, τ:

where Y_o is the quasi-static yield strength (Pa), ε is the strain, (ε^dot) , is the strain rate (s^-1), D and q are constants controlling the strain-rate dependence (determined by fits to experimental strain rate data), B is the strain hardening constant  (Pa) and n is the strain hardening exponent, τ is the thermal softening term:

where T is the physical temperature (K) and T_a is the ambient reference temperature (assumed 300 K) at which the quasi-static yield stress, Y_o, was measured. T_m is the effective melting point (K). Note, as AUTODYN does not use the latent heat of fusion in its calculation of temperature, an effective melting temperature is calculated by taking the latent heat of fusion and dividing by the specific heat capacity and adding that to the literature melting point. This corrects for the problem of materials becoming too soft from being overly thermally softened. The model values for PMMA and Indium are given in Table 1. Finally, in order to stop the yield strength becoming un-physically high at very high strain rates, the maximum yield strength is capped at 5 GPa.

Interestingly, the increase in strength of the PMMA during an impact is controlled almost entirely by strain-hardening, and only has a very weak strain-rate dependence. This is the opposite of indium, which has (at 300 K) virtually no strain hardening. However, it is speculated that at cryogenic temperatures (~150 K) this may no longer be the case, but experiments are required to confirm this. Note: equation-of-state and strength parameters for PMMA were extracted from [8, 9, 10, 11].

How to cite: Price, M., New, J., Spathis, V., Mathies, R., Butterworth, A., and Wozniakiewicz, P.: Modelling of micron-scale impacts into Indium as a soft capture surface: preparing for Enceladus transit, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-37, https://doi.org/10.5194/epsc2020-37, 2020.

Introduction

The smallest Galilean moon Europa is differentiated into an outer ice shell, subsurface ocean, silicate mantle and iron-rich core (J. D. Anderson et al., 1997;  Khurana et al., 1998). Its young surface exhibits a multitude of superposed crosscutting lineaments (Kattenhorn & Hurford, 2009), on some of which a lateral offset of a few kilometres was identified (e.g. Schenk & McKinnon, 1989). On Earth, strike-slip motion, thus potentially lateral offset, occurs either through a primary shear failure or through reactivation of the pre-existing faults and fractures (E. Anderson, 1905). On Europa, the latter case was confirmed so far (Hoppa et al., 1999; Sarid et al., 2002; Kattenhorn, 2004; Rhoden et al., 2012) and a process nicknamed "tidal walking'' (Hoppa et al., 1999) was suggested as a possible mechanism for producing the strike-slip offset through the reactivation of faults via diurnal tidal stresses.

In the simplest setting (see Figure 1), the tension opening the fault facilitates strike-slip motion in one direction, while in the reverse direction in the second half of the period, the motion is suppressed by compression. Consequently, after one period a certain strike-slip offset is accumulated. Our numerical model aims at testing the "tidal walking" model by simulation of the behaviour of Europan strike-slip fault and its surroundings.

Model

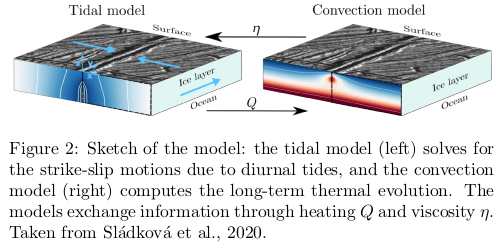
The model consists of two parts reflecting the two timescale nature of the considered process, i.e. the diurnal timescale (~3.5 days) of the forcing stresses and the formation timescale (taken as 100kyr). The tidal model describes the fault and its surroundings as a viscoelastic (Maxwell) body with a pre-existing fissure in the middle of the computational domain, cf. right panel of Figure 2. This model is forced by shear and normal stresses, and it quantifies the tidally-driven heat production. Heat sources are used as an input for the second - convection - model operating on the time scale of tens of thousand years, describing ice as a non-newtonian fluid. The computed thermal evolution affects the viscosity in the tidal model, providing (together with the tidal heating) the coupling between the two modules.

Results

We performed an extensive parametric study of the behaviour of Europan strike-slip fault and its surroundings, varying ice shell thickness (D), the amplitude of loading stresses (shear and normal, σ₀), the phase shift between the shear and normal stresses and the coefficient of friction. The results depend strongly on the amplitude of the loading stresses and the ice shell thickness. Our calculations confirm previous results by Preblich et al., 2007 that the active part of the fault needs to reach a low viscosity zone or to penetrate to the ocean. The whole-shell penetration appears improbable as unrealistically thin (1km) shell and larger than present-day loading stresses would be required. However, our results indicate that a low viscosity zone at the base of the active part of the fault may form as a result of frictional and shear heating in the fault’s vicinity (D=5 km ice shell and σ₀=6 x 10⁵Pa loading amplitude). Such a scenario shows that the thermo-mechanical coupling is vital for the complete understanding of the behaviour of strike-slip faults. A third option for producing observable offset is to assume that the cracks are partially filled with water from the internal ocean, then the hydrostatic pressure is partially compensated by the water column. Thus the active part of the fault can reach the bottom of the shell much more easily, in this setting the production of a significant offset is possible even for the present-date estimates of the tidal forcing amplitudes and ice-shell thickness of less or equal to ten kilometres.

Acknowledgements

The research leading to these results received funding from the Czech Science Foundation through project No. 19-10809S. The computations were carried out in IT4Innovations National Supercomputing Center (project no. LM2015070). The study was supported by the Charles University, project GA UK No. 304217 and SVV 115-09/260581 (K.S.), and by Charles University Research program No. UNCE/SCI/023 (O.S., K.K.). 

References

Anderson, E. (1905). The dynamics of faulting. Transactions of the Edinburgh Geological Society, 8(3), 387–402. doi: 10.1144/transed.8.3.387

Anderson, J. D., Lau, E. L., Sjogren, W. L., Schubert, G., & Moore, W. B. (1997). Europa’s Differentiated Internal Structure: Inferences from Two Galileo Encounters. Science, 276(5316), 1236–1239. doi: https://doi.org/10.1126/science.276.5316.1236

Hoppa, G., Tufts, B. R., Greenberg, R., & Geissler, P. (1999). Strike-slip faults on Europa: Global shear patterns driven by tidal stress. Icarus, 141(2), 287–298. doi:https://doi.org/10.1006/icar.1999.6185


Kattenhorn, S. A. (2004). Strike-slip fault evolution on Europa: Evidence from tail- crack geometries. Icarus, 172(2), 582–602. doi: https://doi.org/10.1016/j.icarus .2004.07.005

Kattenhorn, S. A., & Hurford, T. (2009). Tectonics of Europa. In Europa (pp. 199– 236). University of Arizona Press.

Khurana, K. K., Kivelson, M. G., Stevenson, J. D., Schubert, G., Russell, C. T., Walker, R. J., & Polanskey, C. (1998). Induced magnetic fields as evidence for subsurface oceans in Europa and Callisto. Nature, 424(July). doi: https://doi.org/10.1038/27394

Rhoden, A. R., Wurman, G., Huff, E. M., Manga, M., & Hurford, T. A. (2012). Shell tectonics: A mechanical model for strike-slip displacement on Europa. Icarus, 218(1), 297 - 307. doi: https://doi.org/10.1016/j.icarus.2011.12.015 


Sarid, A. R., Greenberg, R., Hoppa, G. V., Hurford, T. A., Tufts, B., & Geissler, P. (2002). Polar Wander and Surface Convergence of Europa’s Ice Shell: Evidence from a Survey of Strike-Slip Displacement. Icarus, 158(1), 24 - 41. doi: https://doi.org/10.1006/icar.2002.6873

Schenk, P. M., & McKinnon, W. B. (1989). Fault offsets and lateral crustal move- ment on Europa: Evidence for a mobile ice shell. Icarus, 79(1), 75–100. doi: https://doi.org/10.1016/0019-1035(89)90109-7

Sládková, K., Souček, O., Kalousová, K., & Bĕhounková, M. (2020). Tidal walking on Europa's strike slip faults ‐ insight from numerical modeling. Journal of Geophysical Research: Planets, 125, e2019JE006327. https://doi.org/10.1029/2019JE006327

How to cite: Sladkova, K., Souček, O., Kalousová, K., and Běhounková, M.: Tidal walking on Europa's strike slip faults - insight from numerical modeling, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-92, https://doi.org/10.5194/epsc2020-92, 2020.

Introduction

Grooves represent the evidence of tectonic activity that deformed Ganymede surface during its geologic evolution and may have played a key role in the possible connection between surface and the subsurface ocean. In this context, the analysis of Ganymede deformed surface could provide hints regarding its interior, as well as its ice shell’s mechanical behaviour. Indeed, faults distribution and fault populations on icy satellites can reveal insights into the evolution of their surface that cannot be gained with other techniques. In particular, statistical characterization of fault-population attributes, such as length and clustering, are fundamental means to explore deformation rates, stress transmission modes, rheology of the medium, and mechanical layering [1,2,3,4,5]. The fractal analysis has been used in terrestrial planets studies to determine the thickness of the fractured crust [e.g., 6,7,8]. In the same fashion, on icy satellites the exploration of the depth at which fractures penetrate the icy layer could be constrained investigating the main characteristics of fault populations, such as length size-distribution and clustering [9]. In this work, we analyse the grooves’ length and spatial distribution to estimate the potential thickness of the icy crust above the deep ocean required to develop densely populated structures at the surface of Ganymede (i.e. the grooves).

Dataset and Methods

Our analysis is based on the regional scale grooves mapping [10] that represents a useful dataset to improve the knowledge of the tectonic evolution of the satellite and to recognize the main characteristics of these features. Thanks to these comprehensive grooves mapping dataset, we were able to select four different type-regions located on the equatorial belt of Ganymede. The choice is based on the high density and homogeneous spatial distribution of the grooves located on those regions, which is necessary for the following analysis. The four datasets are in selected regions located in Uruk Sulcus, Babylon Sulci, Phrygia Sulcus and Mysia Sulci, respectively. We investigate the main characteristics of Ganymede’s grooves populations on the four different areas analyzing i) the grooves length distribution to describe the propagation and growing evolution of the faults underlying grooves systems. and ii) the grooves self-similar clustering to infer their vertical penetration inside Ganymede icy shell.

Results and Discussion

From the length distribution analysis, we found the presence of both an exponential and power-law trends reflecting the possible coexistence of (i) distributed fault systems, with strain regularly partitioned along evenly spaced faults and confined within specific mechanical layers in the crust (exponential fitting curve/curves) and (ii) localized fault systems, with few large faults cutting across the whole crust (power-law fitting curve) [e.g., 2,4]. From the self-similar clustering analysis, we estimated the potential thickness of the icy crust ranging between 105 and 130 km for the datasets considered. This value agrees with independent estimates of the thickness of the icy shell (from 80 to 150 km, [12,13,14]). Hence, our results support the hypothesis of shorter structures vertically confined in different mechanical layers within the icy crust and few very long faults propagating down to the liquid ocean underneath.

Acknowledgements

The activity has been realized under the ASI-INAF contract 2018-25-HH.0.

References

[1] Benedicto, A et al. (2003), Geophysical Research Letters, 30, 20, 2076.

[2] Soliva, R., and Schultz, R.A., (2008), Tectonics, 27, TC2003.

[3] Gudmundsson, A., et al. (2010), Journal of Structural Geology, 32, 1643-1655.

[4] Schultz, R.A., et al. (2010). In: Planetary Tectonics, Cambridge University Press, 457-510.

[5] Gudmundsson, A., et al. (2013), Tectonophysics, 608, 1298-1309.

[6] Mazzarini F., D’Orazio, M. (2003), Journal of Volcanology and Geothermal Research, v. 125, p. 291-305.

[7] Mazzarini, F., (2004), Geophysical Research Letters, v. 31.

[8] Mazzarini, F., Isola, I. (2010), Geosphere, v. 6, p. 567-582.

[9] Lucchetti, A. et al.,. (2017), Icarus, 297, 252-264.

[10]Rossi, C. et al., (2020) Journal of Maps.

[11] Collins, G.C., et al., 2013. Global geologic map of Ganymede: U.S. Geological Survey Scientific Investigations Map 3237.

[12] Schenk, P.M. (2002), Nature, 417-419, 21.

[13] Kivelson, M.G. et al., 1996. Nature, 384, 537-541.

[14] Saur, J. et al., 2015. JGR Space Physics, 120, 1715-1737.

How to cite: Lucchetti, A., Rossi, C., Mazzarini, F., Pajola, M., Pozzobon, R., Massironi, M., and Cremonese, G.: Length and self-similar clustering analyses of Ganymede’s grooves, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-193, https://doi.org/10.5194/epsc2020-193, 2020.

The gap between Saturn and its innermost D ring is populated with dust particles which primarily originate from the main rings. These particles were sampled by Cassini’s Cosmic Dust Analyzer (CDA) during the final mission phase, providing individual high-speed time-of-flight mass spectra. Compositionally, two main groups were observed, water ice and silicate particles. The relative frequencies of these spectral types vary with distance to Saturn’s ring plane (Hsu et al. 2018).

In this study we present an approach to infer the composition of the silicate particles, which make up nearly 30% of the evaluated spectra, with the aim of deriving the elemental composition of minerals stemming from Saturn’s C and D rings. Owing to CDA’s relatively low mass resolution, spectral peaks from important mineral-forming ions such as Mg⁺, Al⁺ and Si⁺ are often unresolvable individually, forming a single broad peak. To remove this effect, we apply manual deconvolution, enabling the interferences to be disentangled and allowing the relative abundances of the different constituents to be measured. After combining the results of the deconvolution with experimentally-determined relative sensitivity factors (RSFs), converting ion abundances to elemental abundances (Fiege et al. 2014), we are able to infer elemental ratios within the particles and thus quantitatively measure their compositions. The grain detection locations allow C or D ring sources to be discriminated between, and this work represents the first in situ analysis of the rocky fraction in Saturn’s main rings, which until now was only accessible via remote sensing.

Fiege, K., Trieloff, M., Hillier, J. K., Guglielmino, M., Postberg, F., Srama, R., Kempf, S., Blum, J.: Calibration of relative sensitivity factors for impact ionization detectors with high-velocity silicate microparticles, Icarus 241, 2014.

Hsu, H.-W., Schmidt, J., Kempf, S., Postberg, F., Moragas-Klostermeyer, G., Seiß, M., Hoffmann, H., Burton, M., Ye, S.-Y., Kurth, W. S., Horányi, M., Khawaja, N., Spahn, F., Schirdewahn, D., O’Donoghue, J., Moore, L., Cuzzi, J., Jones, G. H., Srama, R.: In situ collection of dust grains falling from Saturn’s rings into its atmosphere, Science 362, 2018.

How to cite: Linti, S., Hillier, J., and Postberg, F.: Compositional analysis of rocky material in Saturn’s C and D Rings as seen by CDA during Cassini’s Grand Finale Orbits, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-359, https://doi.org/10.5194/epsc2020-359, 2020.

The high-speed photometer of Cassini’s Ultraviolet Imaging Spectrograph (UVIS) collected data from stellar occultations across Saturn’s rings at unprecedented high resolution over a wide range of viewing geometries. Because photon counts are described by Poisson statistics, we expect a variance equal to the mean in the absence of intervening ring material. However, most ring ‘particles’ are truly aggregates of smaller particles, ranging from micron-size dust to tens of meter-sized boulders, and if the sizes of these aggregates are not small relative to the field-of-view over a single integration period, they introduce excess variance from which we can glean further information about the sizes of particles and clumps. This is particularly relevant in the A ring, where non-axisymmetric self-gravity wakes are ubiquitous. Larger elongated clumps nicknamed straw have been directly imaged in the troughs of strong density waves (Porco et al., 2005, Science, 307, 1226-1236). In this work we present a survey of the statistical moments of variance and skewness for several ring stellar occultations at two strong density waves from different ring regions, Janus 2:1 and Mimas 5:3, over a variety of viewing angles. The line-of-sight distance from Cassini to the rings affects the measurement area due to the scattered signal and diffraction, and different viewing angles provide measurements of the same ring material with different aspects to potentially reveal the three-dimensional structure of clumps. We calculate an effective particle size per integration area, R, derived by Colwell et al., (2018, Icarus, 300, 150-166) and find similar values for R in both peaks and troughs across density waves as well as within density waves and in adjacent regions. We observe strong statistical similarity between troughs and regions adjoining the waves with overall higher skewness in the A ring, indicating more clumping and greater asymmetry in this region than in the inner B ring region.

How to cite: Eckert, S., Colwell, J., Jerousek, R., and Esposito, L.: Sizes of Particles, Clumps, and Gaps Within the Strong Janus 2:1 and Mimas 5:3 Density Waves from Cassini UVIS Stellar Occultation Data Statistics, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-488, https://doi.org/10.5194/epsc2020-488, 2020.

Introduction: The Cassini mission revealed gas plumes at the south pole of Enceladus that are considered in the context of hydrothermal circulation in the rocky core. We model the internal evolution and differentiation of Enceladus heated by radioactive nuclides and tidal dissipation and investigate core compaction by modeling the evolution of porosity, thereby varying the rock rheology based on different assumptions on the composition.

Model: The model^[2] calculates heating by short- and long-lived radionuclides, latent heat, compaction of porous rock, continuous water-rock separation, redistribution of radionuclides, tidal heating, and water ocean convection. A crucial aspect is the calculation of the core porosity. The core forms by the redistribution of water and silicate particles in a two-phase system after melting of ice. An initial particle agglomerate with interstitial water grows along with an overlying water layer during Enceladus' bottom-up melting. Deformation of the core can lead to a reduction of the pores. The water displaced from them supplies the water layer, while the rock is displaced downward according to the evolution of the porosity. With time it can deform further by creep processes on a geologic timescale. This is modeled by calculating the evolution of the porosity from the change of the strain rate. Here, we use the creep law from [3] that can describe diffusion creep of both “dry” (models A1-A4) and “wet” (models B1-B4) olivine for different values of water fugacity. For a phyllosilicate-rich composition (models C1-C2) supported by plume and E-ring spectral analyses^[4], we use the creep law from [5].

Results: Figure 1 shows the evolution of the structural layers over 4,5 Ga for the model A2 (accretion time of 1,7 Ma), representing successful calculations with the dry olivine rheology. A strong initial temperature increase leads to the onset of melting. The ocean formation starts at ≈3 Ma, with a significant differentiation phase from ≈4 Ma resulting in the formation of an ocean atop a core, finalized by ≈5 Ma after CAIs. During this process, compacting proto-core squeezes a part of the interstitial water through the porous rock into the water layer. The radionuclides are concentrated in the central part of the moon, bringing the central temperature to ≈800 K.

Figure 1: Evolution of the core (dark blue), ocean (yellow), and crust (light blue) shown through the evolution of the heat capacity, since this parameter has considerably different values for all structural layers.

The initial porosity in the ice-rock mixture decreases at ≈2.6 Ma after CAIs throughout the deeper interior at ≈450 K. The displaced water forms an ocean atop of the core. After ≈4 Ma after CAIs the water amount in the central core decreases to 0%. This defines a compact core region upon which a few km thick layer with some interstitial water forms that defines a porous outer core. It is retained because the compaction is not efficient enough to close the pores completely.

Although a liquid layer is retained until present, gradually extincting radionuclides cannot prevent a progressing solidification of the ocean on a global timescale. Additional models (A1-A4, B1-B4, C1-C2) confirm that Enceladus could be far off from a state with a solidified mantle, since a global ocean at present occurs for a variety of parameters. A slowly solidifying ocean shows that, assuming constant orbital conditions, a period of time longer than the age of the solar system must pass until a complete solidification can occur.

Figure 2 shows the water fraction profiles at 4,5 Ga (i.e., at present) in the upper 130 km of Enceladus. A porous outer core is obtained only for wet and dry olivine cores while for an antigorite rheology no porosity is retained.

Figure 2: Final profiles of the water fraction in the upper 130 km for models A1-A4 (dry olivine), B1-B4 (wet olivine), and C1-C2 (antigorite). Note that subduction of a top thin undifferentiated layer, is not modeled.

Conclusions: We modeled the formation and the evolution of an initially porous core and demonstrated the importance of the rheology for its final structure. For both dry and wet olivine core, we could obtain models satisfying conditions for a successful one, in particular, a porous outer core. Compared with different concepts of the core structure discussed in the literature^[6-9], a non-rubble-pile solid but porous structure obtained resembles that derived by [7-9].

A porous outer core obtained for both olivine rheologies supports the hypothesis of hydrothermal circulation of oceanic water. Differing from a sandpile-like structure assumed by [10], a fully consolidated inner core and partially consolidated outer core would result in less tidal heating than suggested by [10]. The assumption of a rubble-pile core made by [11] is inherently closer to our results. However, our calculations show that at least a rubble-pile inner part would be impermanent and a fast consolidation is the ultimate outcome if the core is heated to ≈700 K.

While a porous core layer can generate additional tidal heating^[10,11], this excess heating could catalyze core consolidation, reducing, in turn, the influence of this mechanism. Our results indicate that the amount of heat generated in an unconsolidated core^[10] is an overestimate. From successful models that fit the current understanding of Enceladus’ structure, we constrain the accretion time to 1.3-2.3 Ma. Since an antigorite rheology did not produce successful models with core porosity, it is rather unlikely that the outer core is dominated by this mineral, and the inner core should be dry due to the thermal conditions that facilitate dehydration.

References: [1] Neumann W. et al. (2015) A&A, 584, A117. [2] Neumann W. and Kruse A. (2019) ApJ, 882, 47. [3] Mei S. and Kohlstedt D. L. (2000) JGR, 105, 21457. [4] Postberg F. et al. (2008) Icar, 193, 438. [5] Amiguet E. et al. (2012) EPSL, 345, 142. [6] Schubert G. et al. (2007) Icar, 188, 345. [8] Prialnik E. and Merk R. (2008) Icar, 197, 211. [9] Malamud U. and Prialnik D. (2013) Icar, 225, 763. [10] Malamud U. and Prialnik D. (2016) Icar, 268, 1. [10] Choblet et al. (2017) NatAs, 1, 841. [11] Roberts (2015) Icar, 258, 54.

How to cite: Neumann, W. and Kruse, A.: Modeling the Core Porosity on Enceladus, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-868, https://doi.org/10.5194/epsc2020-868, 2020.

The presence of hydrated minerals at the surface of Europa has been suggested by the measurements of the Galileo Near-Infrared Mapping Spectrometer (NIMS, McCord et al., 2001). Laboratory measurements that best match the observed spectra indicate the presence of magnesium sulfates, sodium carbonates and combinations thereof. The source of these impurities has been suggested to lie beneath the crust in a reservoir rich in dissolved salts.

A recent study using spectral data from the Hubble Space Telescope identified the presence of irradiated sodium chloride at the surface of Europa (Trumbo et al., 2019). This detection correlates with the location of the disrupted chaos terrain, a geologically young region on the leading hemisphere that has been suggested to be formed due to subsurface melting and freezing of the ice shell (Schmidt et al., 2001).

The above listed evidence suggests that the ice shell of Europa may contain a significant amount of contaminants (Kargel et al., 2000; McCord et al., 2001; Zolotov & Kargel, 2009), but their exact distribution is poorly constrained. Previous studies have investigated to which extent the presence of salty components within the ice shell offers an explanation of tectonic surface features of Jupiter’s moon (e.g., Han & Showman, 2005). Yet, how these salt impurities were incorporated into the icy shell and how they evolved over time are still subject of a scientific debate. A rigorous analysis of the transient evolution of salt impurities in the ice shell as well as a better quantification of the amount of salts that can be trapped in the near surface ice layers is necessary.

In this work we investigate the spatial distribution of salts in Europa’s ice shell following a two-fold approach:

First, we consider potential salt in-take processes at the ice-ocean boundary. In a transient regime, hence when the ice-ocean boundary propagates towards greater depths, we can expect a mushy region, composed of an ice matrix bathed in a salt rich liquid (brine). The brine may either be rejected back into the ocean, or it will be trapped in the ice leading to salt inclusions. This process could be efficient during an initial fast freezing phase of the ice shell and might have led to a non-homogeneous distribution of salts within the early ice shell.

Our approach is to explicitly model phase-change and mass flux processes at the ice-ocean boundary on the meso-scale. Meso-scale refers to the fact that the interface model has to be set up on a spatial scale that is much smaller than for a typical geodynamical model. Yet, the scale is still large enough to justify a continuum assumption. Hence, temperature, effective salt concentration and ice volume fraction are modelled as fields. This is in contrast to micro-scale models that might consider individual crystals. Similar approaches are known from the sea ice community (e.g., Buffo, 2018).

A fully self-consistent model that quantifies the influx of salts into the ice shell and applies to both the ice’s initial growth and a well-established, thick ice mantle remains to be developed. Yet, it is possible to investigate the gradual refreezing of a salty ocean, hence the ice-ocean interface propagation speed, in a simplified setting, namely formulated as an extended Stefan type problem that accounts for salt in the water, (e.g., Worster 2000). Our analysis allows us to constrain the refreezing rate as a function of depth and salt content in the ocean. This yields first insights into potentially realistic initial salt distributions in the ice shell as needed for macro-scale geodynamical models. 

In a second part, we employ a macro-scale geodynamical ice shell model to investigate how a certain potentially heterogeneous initial salt distribution in the ice would evolve and re-distribute with time (Fig. 1). In the latter we employ ice relevant rheological parameters (e.g., Durham and Stern, 2001).

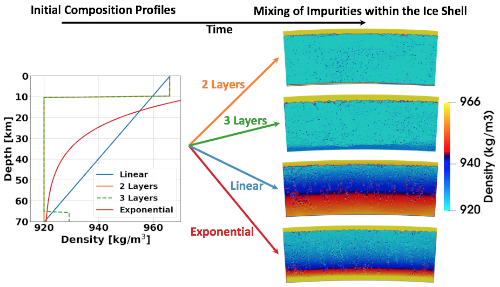
We test under which conditions salts may remain stable close to the surface or are entirely mixed in the ice shell. The presence of salts may affect locally the melting temperature by lowering the melting point by several tens of Kelvin, the buoyancy force due to the higher density of salt rich inclusions, and possibly the viscosity within the ice shell. The mixing efficiency of compositional heterogeneities depends on the relative importance of chemical to thermal buoyancy. If the density contrast between salt rich inclusions and the surrounding ice is dominant such chemical anomalies will sink to the base of the ice shell. If on the other hand the thermal gradient can overcome the compositional gradient, material would mix and convection would redistribute chemical anomalies in the ice shell.

The distribution of salts in the ice shell of Europa is ultimately important for determining whether subsurface brine pockets or mushy regions may be present that if stable over geological time scales, may provide niches for ice shell habitability. Additionally, such regions may be detectable by upcoming measurements from REASON and RIME radars on board the Europa Clipper and JUICE spacecraft (Schroeder et al., 2016; Hussmann et al., 2017).

References:

Buffo, J. J., B. E. Schmidt, & C. Huber, 2018, Journal of Geophysical Research: Oceans 123.1 (2018): 324-345.

Durham, W., & Stern, L. 2001, Annual Review of Earth and Planetary Sciences, 29, 295

Han, L., & Showman, A. P. (2005), Geophysical Research Letters, 32

Hussmann, H., Lingenauber, K., Oberst, J., et al. (2017), in European Planetary Science Congress, Vol. 11

Kargel, J. S., Kaye, J. Z., Head III, J. W., et al. (2000), Icarus, 148, 226

McCord, T. B., Hansen, G. B., & Hibbitts, C. A. (2001), Science, 292, 1523

Schroeder, D. M., Romero-Wolf, A., Carrer, L., et al. (2016), Planetary and Space Science, 134, 52

Schmidt, B., Blankenship, D. D., Patterson, G., & Schenk, P. (2011), Nature, 479, 502

Trumbo, S. K., Brown, M. E., & Hand, K. P. (2019), Science advances, 5, eaaw7123

Worster, G., Moffatt K., & Batchelor G., (2000), ISBN 0521531691, Cambridge University Press, 393 - 411

Zolotov, M. Y., & Kargel, J. S. (2009), in Europa, ed. R. T. Pappalardo, W. B. McKinnon, & K. Khurana (Univ. of Arizona Press), 431–457

How to cite: Plesa, A.-C., Kowalski, J., and Rückriemen-Bez, T.: Compositional convection in Europa’s ice shell: a scale-coupled approach, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1038, https://doi.org/10.5194/epsc2020-1038, 2020.