Poster presentations and abstracts
Session assets
1. Introduction
Origins, Spectral Interpretation, Resource Identification, and Security–Regolith Explorer (OSIRIS-REx) is a NASA New Frontiers mission to return a sample of near-Earth asteroid (101955) Bennu. The OSIRIS-REx spacecraft is equipped with a suite of scientific instruments [1], including the OSIRIS-REx Camera Suite (OCAMS) and the OSIRIS-REx Visible and InfraRed Spectrometer (OVIRS), among others. OCAMS’s high-spatial-resolution images of Bennu’s surface facilitate the identification of regions of interest, characterization of surface morphology, and mapping of relative surface albedo [2]. OVIRS is a point spectrometer that measures surface composition [3]. The OVIRS footprint during the Reconnaissance phase of the mission [1] had an observational field of view with diameters between 5 to 9 m.
We search for and distinguish organics and carbonates on the surface of Bennu by studying the shape of the 3.4-micron feature, as observed by the OVIRS spectrometer during reconnaissance of candidate sampling sites [4]. Aliphatic organics have vibrational stretching bands at 3.4 microns, and the CO32- anion in carbonate minerals has an overtone of a fundamental asymmetric vibrational stretch, also at 3.4 microns. Organics on asteroids are hypothesized to be related to the organic materials delivered to Earth during the early bombardment phase of Earth’s development [5]. Carbonates record evidence of aqueous processes on Bennu [6], and together the organics and carbonates provide evidence for Bennu’s alteration history.
We present the results of a search for Bennu spectral matches to specific laboratory carbonate spectra and meteoritic aliphatic organic spectra, in the wavelength range from 3.2 to 3.6 microns. The carbonate spectra were obtained from the RELAB facility at Brown University [7], and the insoluble organic material (IOM) spectra were obtained from [8]. For the carbonates, we test ~10 representative spectra each of calcite, dolomite, and magnesite. For the organic IOM, we test spectra such as Tagish Lake, Cold Bokkeveld, Mighei, Murchison, and Orgueil.
2 Data collection and preparation
2.1 Spectrum preparation
To prepare laboratory and OVIRS spectra for band-match testing, we first divide every spectrum by a continuum, defined as a second order polynomial. The parabola is constrained using reflectance values at the wavelengths 2.95, 3.24, 3.6 microns. We then “stretch” the band by normalizing each spectrum such that the band minimum occurs at 0.0 and the maximum occurs at 1.0. Thus, we are only comparing the band shapes, as all other quantitative information has been removed by the continuum normalization and the band stretching.
2.2 K-S parameter test
We apply a Kolmogorov-Smirnov (K-S) parameter test to find which laboratory spectra best fit the OVIRS spectra. We compare each laboratory spectrum to the entire OVIRS data set. The K-S parameter is an evaluation of the maximum discrepancy between two cumulative distribution functions (Figure 1). That is, we calculate the cumulative sum of the laboratory and OVIRS spectra and find the points of maximum discrepancy. The smaller the discrepancy, the better the fit.
3 Results
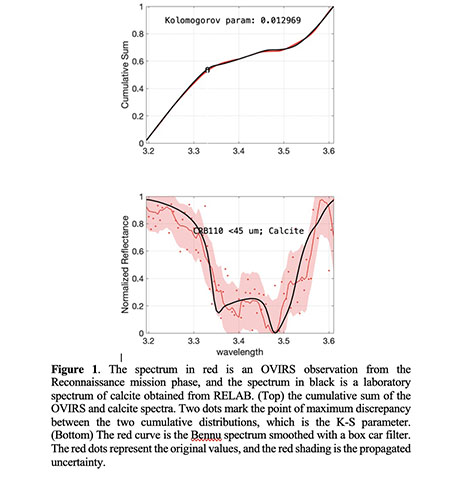
Figure 1 shows an example match between an OVIRS spectrum from Bennu and a laboratory spectrum of calcite. Because the K-S parameter has a very low value (<0.013), we consider this a strong calcite detection. We perform the same test for the different types of carbonates and detect calcite more frequently than dolomite or magnesite. We perform the K-S test for all different types of IOM in our spectral library, and we find good matches on Bennu for the IOM in the Tagish Lake, Cold Bokkeveld, Mighei, Murchison, and Orgueil meteorites.
We will present maps of where carbonate and organic material is detected on Bennu and discuss our search for associations or correlations with boulders or other surface properties.
Acknowledgements
This material is based upon work supported by NASA under Contract NNM10AA11C issued through the New Frontiers Program. INAF participation was supported by Italian Space Agency grant agreement n. 2017-37-H.0. We are grateful to the entire OSIRIS-REx Team for making the encounter with Bennu possible.
References
[1] Lauretta, D.S. et al. (2017). OSIRIS-REx: Sample Return from Asteroid (101955) Bennu. Space Sci. Rev. 212, 925–984.
[2] Rizk, B. et al. OCAMS: the OSIRIS-REx camera suite. Space Sci Rev (2018) 214:26 https://doi.org/10.1007/s11214-017-0460-7
[3] Reuter, D.C. et al. (2018). The OSIRIS-REx Visible and InfraRed Spectrometer (OVIRS): Spectral Maps of the Asteroid Bennu. Space Sci. Rev. 214, 54.
[4] V. E. Hamilton. VNIR-TIR spectroscopy of (101955) Bennu. This conference.
[5] Anders, Edward. Pre-biotic organic matter from comets and asteroids. Nature 342.6247 (1989): 255-257.
[6] Kaplan, H. H., et al. Evidence of Organics and Carbonates on (101955) Bennu. LPI 2326 (2020): 1050.
[7] Pieters, C.M., et al. Reflectance Experiment Laboratory (RELAB) Description and User's Manual. NASA Technical Reports Server. (2004). Document ID, 20040129713
[8] Kaplan, H.H., et al. Reflectance spectroscopy of insoluble organic matter (IOM) and carbonaceous meteorites. Meteorit Planet Sci, 54 (2019): 1051-1068. doi:10.1111/maps.13264
How to cite: Ferrone, S., Clark, B., Kaplan, H., Zou, X.-D., Li, J.-Y., Barucci, A., Simon, A., Hamilton, E., Reuter, D., Praet, A., Deshapriya, P., Poggiali, G., Brucato, J., and Lauretta, D.: Distinguishing carbonates and organics on OSIRIS-REx target asteroid Bennu using the 3.4-micron feature, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-165, https://doi.org/10.5194/epsc2020-165, 2020.
Modeling Bennu’s Crater Development
P.H. Smith (1), D.N. DellaGiustina (1), K.N. Burke (1), D.R. Golish (1), D. S. Lauretta (1)
(1) Lunar and Planetary Laboratory, University of Arizona, USA (psmith@lpl.arizona.edu)
Introduction
Several hundred craters have been identified and mapped on Bennu [1]. Their spectral properties have been studied using data from the MapCam instrument onboard the OSIRIS-REx spacecraft [2]. The crater frequency versus spectral slope across the wavelength range of 0.550 µm (v band) to 0.860 µm (x band) shows a skewed distribution varying from the median spectral slope of –0.17 micron–1 (x/v = 0.948) to a neutral or flat slope (x/v = 1.0). DellaGiustina et al. [2] attribute this trend to space weathering. They suggest that freshly formed craters are red, and as they age, they evolve to the bluish slope seen across the asteroidal surface. This abstract presents the results of an age model of Bennu’s craters in the size range of 1 to 10 m. Craters in this size range were selected as having likely been formed during the time that Bennu has orbited in near-Earth space. Larger craters on Bennu are thought to have formed during its long history in the main asteroid belt [3].
Elements of the Crater Model
Our model covers three stages in the evolution of craters. First, a creation function produces a small number of craters randomly selected for size according to a power law distribution. These craters appear each time step. Because the modeled crater distribution will be compared to the measured one, an uncertainty is introduced into the color slope. In other words, at each time step, craters form with an x/v of 1.0±0.01 and with sizes randomly drawn from a power law distribution (radius–3).
Once a crater is created, it is tracked throughout its evolution. With each time step, the crater weathers toward a bluish slope. The number of time steps required is determined through an exponential function whose 1/e time is a variable in the model. The slope decreases rapidly at first but approaches the final Bennu slope asymptotically. This is the final destination for stages one and two.
The third stage is the erasure of craters. This can occur through mass wasting that is either gravitationally forced or caused by impact-driven seismic shaking [4]. OSIRIS-REx has observed particles thrown off into orbit that return to the surface, which may also contribute to erasure [5]. Because of the limited observational data concerning these processes, they are modeled together in a linear fashion such that the smaller craters have shorter lifetimes than the larger ones. The slope of this fill-in rate is a variable in the model.
The code runs time step by time step, and all craters are tracked throughout their lifetime. The variables are optimized so that the spectral slope distribution matches that observed.
Model Results
Figure 1 illustrates a typical output of the model. The variables are set in the following manner: The 1/e time for weathering is 50 time steps. The erasure algorithm starts eliminating the smallest craters after an age of 160 time steps and will eliminate all craters <10 m after 1600 time steps. The final part of this exercise is estimating the length of a time step.
Judging from [6], 26 impacts/year with a typical crater diameter of 14 cm could have produced the observed particles leaving Bennu. Putting this observed flux onto a size distribution power law curve suggests that a time step on the order of 1000 years would produce several 1-m craters. Therefore, using a time step of 1000 years, the weathering time for all craters is about 150,000 years (3 times the 1/e value). The erasure rates are size-dependent: 1-m craters “live” about 160,000 years; 10 m craters survive about 1.6 million years. New craters are always forming replacing the ones that have been erased.
These values are meant to be illustrative rather than accurate. They show a pathway for the creation of a skewed size distribution where we observe that the freshest-looking craters are reddish while the older ones match Bennu’s average blue slope.
Acknowledgments
This material is based upon work supported by NASA under Contract NNM10AA11C issued through the New Frontiers Program. We are grateful to the entire OSIRIS-REx Team for making the encounter with Bennu possible.
References
[1] Bierhaus, E.B. et al., 51st Lunar and Planetary Science Conference (2020) [2] DellaGiustina, D.N. et al., this meeting. [3] Walsh, K.J. et al., Nature Geoscience, 12, 242-246 (2019) [4] Richardson, J.E. et al., Science, 26,1526-1529 (2004). [5] McMahon, J.W. et al., JGR Planets, doi: 10.1029/2019JE006229. [6] Bottke, W.F. et al., JGR Planets, doi: 10.1029/2019JE006282
(2020).
How to cite: Smith, P., DellaGiustina, D., Burke, K., Golish, D., and Lauretta, D.: Modelling Bennu's Crater Development, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-442, https://doi.org/10.5194/epsc2020-442, 2020.
Introduction: The phenomenon of landslide is a form of the gravity movement. Comets have weak gravity field, so it is believed that probability of landslides is very low. However observations from space missions to comets 9P/Tempe 1 and 67P/Churyumov – Gerasimenko revealed existence of these mass motion.
The causes of landslides are usually related to instabilities of slopes. It is often possible to indicate a few causes of the landslide but usually only one factor is considered to be a trigger. Causes are the factors responsible for making the slope unstable in respect to small disturbances. Some causes could also trigger landslides [1].
In the present paper we consider comet 67P/Churyumov–Gerasimenko. Investigation of its nucleus indicated existence of deposits typical for landslides. In previous works we consider ejecta from some places of the comets. In presen paper we investigate stability of ejecta in the place of landing.
Slopes of the surface:
On the small bodies of spherical shape the area with large slope (in respect to the local gravity) is rather limited. The different situation could be observed on highly asymmetric bodies [2].
The gravitational field of 67P/Churyumov–Gerasimenko comet is very complicated. There are several regions of different slopes of the physical surface in respect to the gravity. The most of the surface (~74%) has the slope in the range 0< α<40o. The slope in the range 40o < α<70o is found on ~17% of the surface.
Fig. 1. Assumed mass distribution in the comet (green volume) and the surface of the constant value of the gravitational potential (red surface) for -0.45 m2 s-2. The green surface contains mass used for the modelling the gravity of the comet and it is close (but not identical) to the physical surface of the comet.
Mechanism of ejection
We followour previous works, we use a simple model of processes leading to the formation of slow ejecta – Fig. 2. The phase transition heats a certain underground volume [3, 4]. It leads to vaporization of volatiles. Eventually a cavity is formed. If the pressure in the cavity exceeds some critical value then the crust could be crushed and its fragments will be ejected in space.
Fig. 2. A simple model of processes leading to the formation of slow ejecta.
The trajectories of test particles ejected with the velocity 0.7 m s-1 from different parts of Imhoteb are given in Fig. 3. Note that ejecta are deposited mainly in two different regions, one in the large lobe and another in the small lobe.
Fig. 3 The trajectories of motion of the matter ejected from Imhotep (on the large lobe) with the velocity 0.7 m s-1.
Results and conclusions
Ejecta landing on the highly inclined surface could trigger another landslide. It depend on angles of landing and the properties of the material of the comet.Let consider the fate of a dry single grain. If comet material could be treated as dirty snow then non-elastic behaviour seems to be most probable. We have performed several calculations of motion of test particles after landing assuming fully non-elastic collision, therefore test particles have only tangential component of velocity after impact (see Fig. 4 upper part). Under this assumption a friction coefficient of grains and surface seems to be the only unknown parameter of motion. The angle of repose for many loose materials is in the range ~35o, (e.g. for dry quartz sand it is 34o) – e.g. Nichols and Franklin (1898). This corresponds to value for coefficient of friction of ~0.7. Unfortunately this approach is rather unrealistic. Note that the slope of face of tetrahedrons represent only average slope of the physical surface.
Fig. 4. Upper part – an ‘ideal’ situation: on smooth surface of comet (given by a face of the shape model) the fate of ejecta after landing depends on: friction coefficient, inclination of the place of landing in respect to the local gravity g, angle between the vector of velocity v (or vector of momentum p) and the normal to the surface. Large angles could lead to developing a new landslide (regular or ballistic). However the true motion is determined by small scale details of the comet's surface as well as shape and amount of grains – lower part.
The motion of grains is not determined by this average slope and average coefficient of friction. The small-scale effects are decisive. The grain can slide over the entire face if it overcome the worst obstacle on the face. For grains of the shape and size shown in lower part of Figure 4, the worst obstacle is the vertical obstacle B. To break it, the sliding grain must have enough kinetic energy to crush the obstacle. Obstacle A could be overcome but it requires more energy than sliding along an ‘ideal’ smooth face. Note that we do not have data about these critical small scale obstacles. Moreover, the size and shapes of grains are also important as well as the thickness of the deposited layer. Eventually, in realistic calculation we cannot assume ~0.7 as an effective value of coefficient of friction. We must assume significantly higher value. For values from the range 1-1.5 only a few particles move from their landing face to another face. Most of them are stopped later. For thick deposit layer different approach is necessary – the thick layer could make the face more smooth. In such a case futher motion is possible. Therefore for landslides of large volume one cannot treat the landslide as a motion of single test particle.
Acknowledgements: The research is partly supported by Poland's National Science Center (Narodowe Centrrum Nauki) [decision No. 2018/31/B/ST 10/00169].
References
[1] Czechowski L., (2016) LPSC 2016, 2781 pdf.
[2] Czechowski L., (2017) EGU 2017 April, 26, 2017
[3] Kossacki K., Czechowski L., 2018, Icarus vol. 305, pp. 1-14, doi: 10.1016/j.icarus.2017.12.027
[4] Kossacki, K.J., Szutowicz, S., 2010, Icarus 207, 320- 340.
[5] Czechowski L. and Kossacki K.J. 2019. Dynamics of material ejected from depression Hatmehit. Submitted.
How to cite: Czechowski, L. and Kossacki, K.: Landslides on Comet 67P/Churyumov–Gerasimenko: Stability of Ejecta in Places of their Depositions, Europlanet Science Congress 2020, online, 21 Sep–9 Oct 2020, EPSC2020-1081, https://doi.org/10.5194/epsc2020-1081, 2020.
