QuACK: Quincuncial Adaptive Closed Kohonen maps for ducks and other odd shapes

A self-organizing Kohonen map is a special type of artificial neural network. The neurons are arranged in a rectangular grid, so each neuron can be identified by two indices i and j. Besides its indices, each neuron carries a float vector. The network learns these vectors from randomly presented sample values. It evolves into a topologically correct two-dimensional map of the input data set.

The network is initialized with small random values for each neuron. It is then optimized by repeatedly iterating through the following steps:

• Randomly choose a vector r from the input data set.
• Find the neuron (i,j) whose vector r_i,j is closest to r in Euclidean distance r_i,j−r.
• Move the vector r_i,j towards r some fraction γ, γ≤1, of the distance, so the new value becomes

  r′i,j = ri,j + γ ( r − ri,j ) .     (1)

• Also move the vectors r_k,l of neurons (k,l) in the vicinity of (i,j) towards r, but weighted with a factor that decreases with the distance from (i,j), where the distance d is measured on the two dimensional map, i. e.,

  d = ((k−i)2+(l−j)2)1/2.     (2)

  With a Gaussian for the weighting factors, the updated vectors become

  r′k,l = rk,l + γ  exp(−d2/σ2)  ( r − rk,l )     (3)

  with some reach σ.

Step 4 ensures the formation of a topologically correct map. The parameters γ and σ have slowly to be turned down to zero towards the end of the optimization, the former to prevent noise introduced by the randomly selected input data, the latter to avoid excessive smoothing.

One application of such a self-optimizing Kohonen map is the mapping of the surface of a three-dimensional shape, like comet 67P/Churyumov-Gerasimenko, see Fig. 1.

 

Figure 1: Shape model of comet 67P/Churyumov-Gerasimenko.

 

As input data, we use the three-dimensional positions of shape model vertices. The result of fitting a low resolution toy model to 67P is shown in Fig. 2.

 

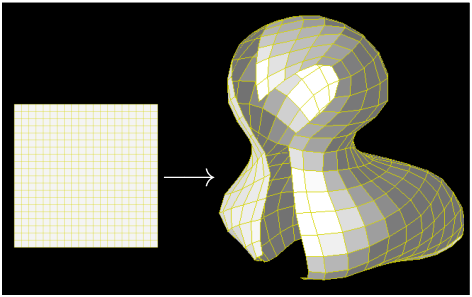
Figure 2: Fitting a toy model of 21×21 neurons to the shape of comet 67P. This is just for illustration. The real map has much higher resolution.

 

The map tries to sample the surface of the shape as evenly as possible. As a consequence, there is a gap between the edges of the map where they fold towards each other. The gap narrows with increasing resolution, however, by fitting a closed surface, see Fig. 3 we can avoid the gap at all. Moreover, the resultant map inherits the tessellation properties of the topologically equivalent Peirce quincuncial projection.

 

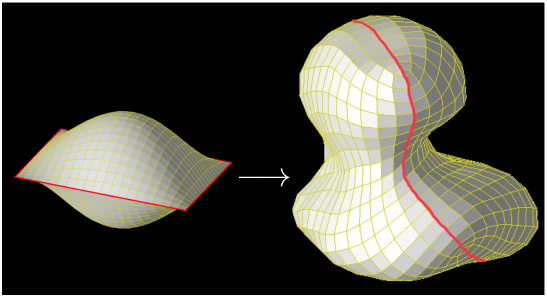
Figure 3: We construct a closed surface from two square grids of neurons connected at all four edges. This neural network learns the shape in the same way as the classical Kohonen map, however, it covers the complete surface without any gap. Again the real map has much higher resolution as this toy model.

 

The resultant map is a shape model of 67P in its own right, albeit with relatively low resolution (the full scale model has 160,000 plates). But this shape model has the very special property that it can be unfolded to a two dimensional map. The are different possibilities how the closed structure is cut open and unfolded. One is illustrated in Fig. 4.

 

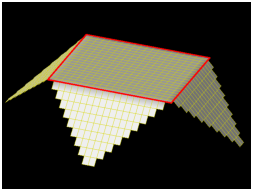
Figure 4: Unfolding of the closed surface into a two dimensional square map in quincuncial layout, which resembles the Peirce quincuncial projection of the world.

 

In this way, we obtain the Quincuncial Adaptive Closed Kohonen (QuACK) map of comet 67P.

Any features on the surface of comet 67P can be projected onto the QuACK map. While the QuACK map has limited resolution (although much higher than the toy model illustrations shown here), features can be mapped with subgrid accuracy employing bilinear interpolation. An example of a geological QuACK map is shown in Fig. 5.

 

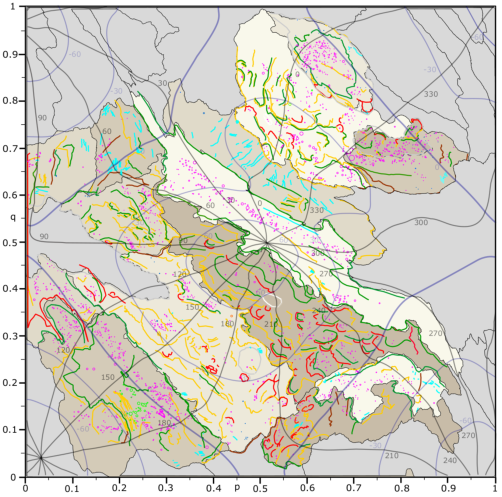
Figure 5: Example geological map of 67P in the QuACK map projection, from Leon-Dasi, M., S. Besse, B. Grieger and M. Küppers (2021).