Formation of lunar megaregolith: the preservation of ancient impact boulders

1. Introduction
Numerous large impacts during the early bombardment period resulted in a globally fragmented crust known as lunar megaregolith (Hartmann 2019). Understanding how megaregolith evolved from an initially intact crust is important for the thermal and magmatic evolution of the Moon (Jaeger et al., 2007; Melosh, 2011; Warren & Rasmussen, 1987) and interpretations of lunar samples. In this study, we developed a spatial-resolved numerical model of the formation of the lunar megaregolith characterized by a size-frequency distribution of fragments generated by a continuous impactor flux. 
2. Model
2.1 Crater distribution
We use the typical “accretion tail” model of early intense bombardment to calculate the crater distribution (Neukum 1989). The considered minimum crater diameter is assumed to be the diameter of saturated craters of the lunar highlands (>20 km; Head et al 2010) where 100% of the surface is covered by craters larger than this size. Thirty basin-forming events with a model age after Orgel et al. (2018) are included in our simulations. 
2.2 Fragment size distribution of individual impacts
2.2.1 Fragment size in ejecta
The size distribution of fragments in ejected materials is simulated by assuming that the distal ejecta deposits contain smaller fragments while ensuring the ejecta thickness, H(r), follows the power-law according to Pike (1974), H(r)=0.033R_t(r/R_t)^-3, where r is the distance from the crater center, and R_t is the radius of transient crater diameter.
Crater ejecta deposits are composed of rock fragments of various sizes. The cumulative number N(m) of fragments of mass equal to or greater than mass m is (Melosh 1989): N(m) = C₁m^-b, where C₁ is a constant. The value of b depends upon the fragmentation process, and for multiple fragmentations, b near 1.0 (Melosh 1989; Buhl et al. 2014). The largest fragments are usually near the crater rim. The relation between maximum block size lE and crater diameter (D) (Moore 1971) is: l_E = C₂ D^2/3, where C₂ is constant with a value ranging from 0.1 to 0.3.
2.2.2 Fragment size below the crater 
Melosh (1979) proposed the so-called Acoustic Fluidisation model to explain the temporary weakening of rocks during crater formation. The simplified variant, the Block model (Melosh & Ivonov 1999) describes the rheology of temporarily weakened rocks by a Bingham viscosity which depends on the average block size (l_B0), the viscosity η, the target density ρ, and the average period of the oscillations T. Acoustic wave can only induce shaking of blocks, resulting in acoustically fluidized behavior, if the oscillation wavelength λ (λ=T×c_s, where c_s is the speed of sound) is comparable to the l_B0. For simplicity we assume l_B0 = λ.  
η=2πρl_B0²/T (1)
Since the impact of a large projectile leads to larger blocks and higher viscosity than smaller impactors, Wünnemann et al. (2003) proposed a scale dependency of the viscosity  according to linear relationship:
η= γ_η (c_s ρ D_P⁄2) (2)
where γ_ηis dimensionless scaling parameter and is assumed to be 0.005 (Martellato et al. 2018). Combining eq. 1 & 2 results in:
l_B0=(γ_η D_P)⁄4π 
In the Block model the block or fragment size (l_B0) is usually taken to be constant through space, and the variations of block sizes concerning the distance from the point of impact are neglected. Based on the well-exposed Upheaval Dome crater, Kenkmann et al. (2006) suggested a linear function of the block size (l_B) with the distance from the crater center (r_B), where the function slope, C₃, is ~0.4. Assuming lB0 to be representative for the fragment size close to the crater floor, the block size distribution beneath the crater with the distance from crater center can then be calculated: 
l_B=l_B0+C₃ r_B
3. Results
3.1 Formation of megaregolith
Figure 1 presents the globally volume-weighted fragment size distribution with depth at different times. Basin-forming events are the dominant factor generating a global megaregolith layer. After the formation of the youngest basin (3.8 Ga), the big picture of the megaregolith was established. In the later period (e.g., 3.7 Ga; black dots in Figure 1), the smaller-scale impacts were predominant and could not significantly alter the megaregolith structure anymore. The generated megaregolith displays two distinct layers: an Upper Megaregolith that mainly consists of ejected fragments with smaller size and a thickness of ~2.5 km; a Lower Megaregolith that mainly consists of autochthonous fragments with a thickness of more than 10s of kilometers. The obtained structure of the megaregolith is consistent with both the lunar seismic and gravity observations.

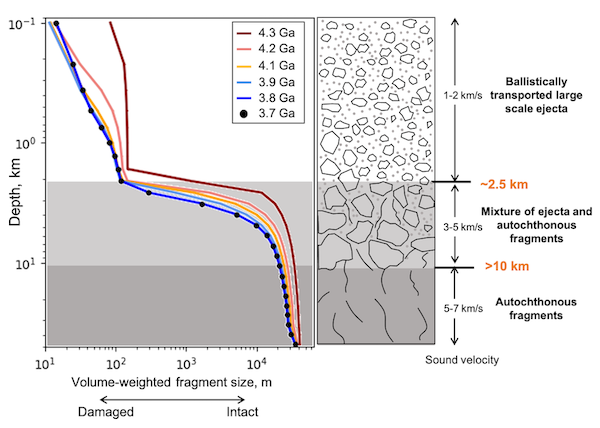
Figure 1 Formation and structure of the megaregolith.
3.2 Presence of SPA ejecta boulders
When the South Pole-Aitken (SPA) was formed, its excavated fragments distributed over the global surface. These fragments suffered further fragmentation altering their size and spatial distribution. When the structure of the megaregolith was formed (3.8 Ga), the majority of the SPA ejecta fragments became very small. Due to subsequent space weathering, almost no boulders < 50 m can survive for 3.8 Ga (Basilevsky et al. 2013). We estimated the distribution of the >50 m SPA ejected fragments in the near-surface shown in Figure 2. Less than 5% of SPA ejected boulders could have survived until the present day and the majority of the survival is distributed near the rim of young and large impact craters. 

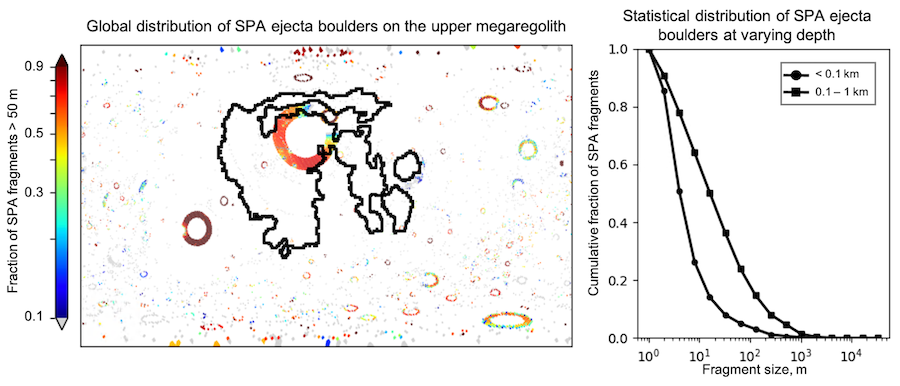
Figure 2 Distribution of SPA ejecta boulders when the megaregolith was formed.
4. Conclusions
A spatial-resolved numerical model was developed to investigate the cumulative fragmentation process on the moon aiming at a quantitative description of the formation of megaregolith. We found that after the cessation time of basin-forming events, the structure of megaregolith was established. The megaregolith possesses a distinct two-layer structure:  a more fragmented Upper megaregolith ~2.5 km in thickness that mainly consists of the ejected fragments and a Lower megaregolith >10 km in thickness that mainly consists of autochthonous fragments. The simulation results also suggest that most of the ancient impact fragments, such as boulders ejected upon formation of SPA, cannot survive until the present day.