Deep learning for surrogate modelling of 2D mantle convection

Introduction

Mantle convection is a key driver of the long-term thermal evolution of terrestrial planets. Caused by the buoyancy-driven creeping flow of silicate rocks, mantle convection can be quantified through equations of conservation of mass, momentum and energy. These non-linear partial differential equations are solved through fluid dynamics codes such as GAIA [1]. However, the key parameters to these equations are poorly constrained. While the input parameters to the simulations are unknown, the outputs can sometimes be observed directly or indirectly using geophysical and geochemical data obtained via planetary space missions. Hence, the “observables” can be used to constrain parameters governing mantle convection. 

Given the computational cost of running each forward model in 2D or 3D (on the scale of hours to days), it is often impractical to run several thousands of simulations to determine which parameters can satisfy a set of given observational constraints. Traditionally, scaling laws have been used as a low-fidelity alternative to overcome this computational bottleneck. However, they are limited in the amount of physics they can capture and only predict mean quantities such as surface heat flux and mantle temperature instead of spatio-temporally resolved flows. Using a dataset of 2D mantle convection simulations for a Mars-like planet, [2] showed that feedforward neural networks are capable of taking five key input parameters and predicting the entire 1D temperature profile of the mantle at any given time during the 4.5-Gyr-long evolution of the planet.  Using the same dataset of forward models run on a quarter-cylindrical grid, we show that deep learning can be used to reliably predict the entire 2D temperature field at any point in the evolution. 

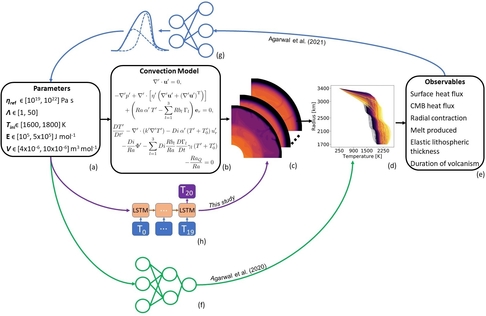
Fig. 1: Machine learning methods have been shown to work well for these low-dimensional observables such as the 1D temperature profile or components derived from it such as surface heat flux or elastic lithospheric thickness, both - (f) in a forward study ([2]) and (g) an inverse study ([3]). In this work, we demonstrate that (h) a surrogate can model 2D mantle convection using deep learning. 

 

Setup of mantle convection simulations

The mantle is modeled as a viscous fluid with infinite Prandtl number and Newtonian rheology under the extended Boussinesq approximation. The thermal expansivity and thermal conductivity are pressure- and temperature-dependent. Same applies to the viscosity, which is calculated using the Arrhenius law for diffusion creep. The bulk abundances of radiogenic elements are modified via a crustal enrichment factor, assuming that a crust of a fixed thickness formed very early in the evolution. Partial melting depletes heat-producing elements in the mantle and affects the energy balance. Finally, we add two phase-transitions in the olivine system. For a detailed description of the methods used, we refer to [2] and the references therein.

 

Compression of temperature fields

Each temperature field is of the size 302 x 394 grid points, making it a difficult task to predict such a high dimensional field from a limited amount of data. Hence, we first use convolutional autoencoders to compress each temperature field by a factor of 140 to a latent space representation, which is easier to predict (Fig. 2). 

 

Fig. 2: Convolutional autoencoders are used to compress the temperature fields by a factor of 140 to a so-called “latent space”. When constructed back to the original size, one can compute the difference between the original and the reconstructed field and use it to optimize the network weights.

 

Prediction of compressed temperature fields

As in [2], we test feedforward neural networks (FNN) to predict the compressed temperature fields from five input parameters plus time. We found that while the mean accuracy of the predictions relative to GAIA temperature fields was high (99.30%), FNN was unable to capture the sharper downwelling structures and their advection. The FNN fails to capture the rich temporal dynamics of convecting plumes and downwellings as the network only sees disconnected snapshots from different simulations (Fig. 3, upper panels).

To address this, we tested long short-term memory networks (LSTM), which have recently been shown to work in a variety of fluid dynamics problems (e.g. [4]). In comparison to the FNN, LSTM achieved a slightly lower mean relative accuracy, but captured the spatio-temporal dynamics much more accurately. The LSTM not only captures the downwellings, but also their advection in time (Fig. 3, lower panels). 

 

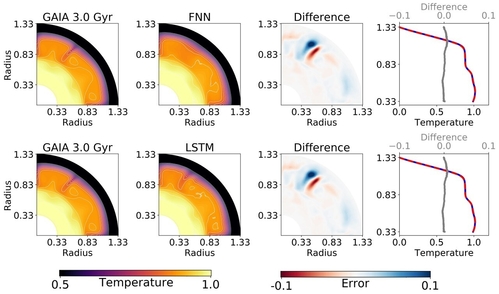
Fig. 3: Predictions from FNN (row 1) vs. LSTM (row 2), when compared with an  original GAIA simulation (column 1) in the test-set. Column 3 shows the difference between predicted and original temperature field, while column 4 shows the horizontally-averaged 1D temperature profiles from GAIA (solid blue) and from the machine learning algorithm (dashed red) as well as the difference between the two (grey line).

 

A proper orthogonal decomposition (POD) analysis (e.g. [5]) of the example simulation in the test-set shows that eigenfrequencies of the FNN predictions decay rapidly after only the first three to five modes. On the contrary, LSTM predictions are more energetic and hence, capture the flow dynamics more accurately (Fig. 4).

 

Fig. 4: Eigenfrequencies obtained through POD of the example simulation in the test-set.

References

1. C. Hüttig, N. Tosi, W. B. Moore, An improved formulation of the incompressible Navier–Stokes equations with variable viscosity, Physics of the Earth and Planetary Interiors, Volume 220, 2013, Pages 11-18, https://doi.org/10.1016/j.pepi.2013.04.002.

2. S. Agarwal, N. Tosi, D. Breuer, S. Padovan, P. Kessel, G. Montavon, A machine-learning-based surrogate model of Mars’ thermal evolution, Geophysical Journal International, Volume 222, Issue 3, September 2020, Pages 1656–1670, https://doi.org/10.1093/gji/ggaa234.

3. S. Agarwal, N. Tosi, P. Kessel, S. Padovan, D. Breuer, G. Montavon (2021). Toward constraining Mars' thermal evolution using machine learning. Earth and Space Science, 8, e2020EA001484. https://doi.org/10.1029/2020EA001484

4. Arvind T. Mohan, Dima Tretiak, Misha Chertkov & Daniel Livescu (2020). Spatio-temporal deep learning models of 3D turbulence with physics informed diagnostics, Journal of Turbulence, 21:9-10, 484-524. 10.1080/14685248.2020.1832230

5. L. Brunton and J. N. Kutz, 7 data-driven methods for reduced-order modeling, in Snapshot-Based Methods and Algorithms, edited by P. Benner, S. Grivet-Talocia, A. Quarteroni, G. Rozza, W. Schilders, and L. M. Silveira (De Gruyter, 2020)