Resonance confinement of collisional particle rings

We have performed numerical simulations of narrow rings around small bodies, addressing both the m=2 resonance perturbations induced by a rotating tri-axial ellipsoidal central body and the m=1 perturbations due to a mass anomaly on the surface of the central body.  The simulations include up to 1e5 mutually colliding particles, and their partially inelastic impacts are resolved with the soft-sphere treatment introduced in Salo (1995; for details see Salo et al. 2018). An azimuthally complete ring is followed, and the integrations are performed in an inertial center-of-mass frame, lasting up to 1e5 central body rotations. Our goal is to see under which conditions the perturbation may prevent the collision-induced viscous spreading of the ring, instead leading to a confinement.

Our study is motivated by the narrow dense rings discovered around the tri-axial Centaur object Chariklo (Braga-Ribas et al. 2014) and the dwarf planet Haumea (Ortiz et al. 2017). In particular the Chariklo ring consists of two narrow components, with the inner ring having an optical depth of the order of unity and possessing sharp edges. While the ellipticity of the ring is poorly constrained (measurements are consistent with a circular ring), it is known to exhibit substantial width variations (Berard et al. AJ, 154, 144). Both Chariklo and Haumea rings are close to a distance where the orbital period equals three central body rotations, corresponding to a 2/6 resonance with a rotating ellipsoidal body, and a 1/3 resonance for a mass anomaly (Sicardy et al. 2019).

Sicardy et al. (2019) demonstrated that torques connected to resonances lead to a rapid clearing of particles from the vicinity of the central body, up to distances where orbital period equals two central body rotation periods.  Their test particle calculations approximated the effects of impacts with an additional Stokes friction term.  Our realistic collisional simulations confirm these results, and also indicate that the m=2 perturbation by the ellipsoidal body has an insignificant effect at the 2/6 resonance. On the other hand, we find that a sufficiently strong mass anomaly may eventually lead to formation of a narrow confined ring near 1/3  (Fig. 1).

What maintains the ring confined?  Our favored mechanism is the reversal of angular momentum flux.  Without perturbation, the outward flow of angular momentum, together with collisional dissipation, always implies radial dispersal of a narrow ring. However, in a strongly perturbed ring (say with an eccentricity gradient related to width variations) the direction of flux may reverse, leading to a confinement of sharp edges (Borderies et al. 1982).  In Hänninen and Salo (1994, 1995; see also Goldreich et al 1995) such a confinement was verified in direct simulations of first order satellite Lindblad resonances, including the inner 2/1 (ILR) and outer 1/2 (OLR). Moreover, the
simulation-measured pressure tensor was shown to be in accordance with the theoretical mechanism.  With the current code we have verified this early simulation result, and extended similar measurements to the 1/3 case.  However, the 1/3 behaviour is more complicated due to the different order of the resonance.  While in the ILR and OLR resonances the response of the ring is more or less steady in the frame rotating with the perturber, this is not so in the 1/3 case.

We are currently investigating in detail the confinement/ flux reversal mechanism, which results will be reported.  We will also discuss the scaling between the simulated particle size and the magnitude of the mass anomaly required for confinement.  Eventually,  in order to extend the calculations to realistic particle sizes, a larger number of particles needs to be simulated in a multi-processor environment: for that purpose we plan to use the new REBOUND-based soft-sphere code recently applied to local simulations of viscous overstability (Mondino-Llermanos and Salo, this meeting; submitted to MNRAS).  The soft-sphere impact treatment is important as the ringlets have a large optical depth; it will also facilitate the later inclusion of ring self-gravity, important for rings near the Roche zone where temporary clumping of particles is expected.

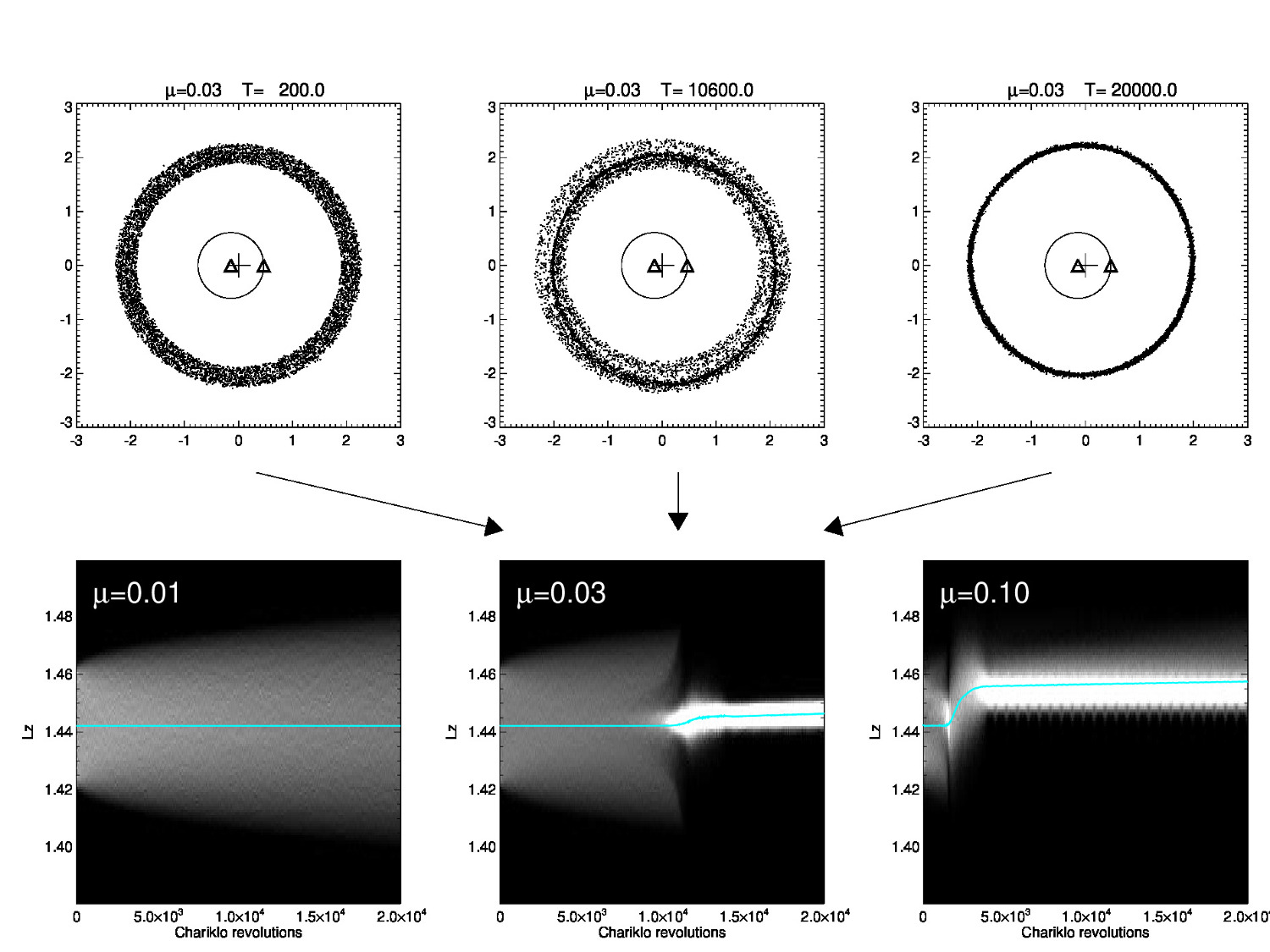
Figure 1.

Upper row: evolution of a ring around a spherical central body with a mass anomaly μ=0.03. Three snapshots of the ring are shown: the title indicates the time in terms of central body rotations. The ring is initially centered at the 1/3 resonance (2.08 times the corotation distance) and  the size of the simulated particles corresponds to about 200 meters when scaled to the Chariklo system.  In the plot the radial deviations from the resonance distance are exaggerated by a factor of three. Triangles indicate the locations of the central body and the mass anomaly, while  the cross indicates the center-of-mass: for clarity, the deviations are exaggerated by a factor of 10.  

Lower row: evolution of the distribution and mean value of angular momentum L_z, in three simulations with different μ. With μ=0.01 the perturbation is too weak to prevent the collisional spreading of the ring. With μ=0.03 (same simulation as in the upper row) and μ=0.1 the particle orbits gradually get organized in the vicinity of the resonance and eventually experience a rapid excitement of eccentricities accompanied by an outward drift in Lz. After resonance passage the eccentricities are damped and the particles form a narrow ringlet with confined sharp edges.

 

References:

  Berard et al. 2017, AJ 154, 144.   Borderies et al. 1982, Nature 299, 209.   Braga-Ribas et al. 2014, Nature 508, 72.   Goldreich et al., 1995, Icarus 118, 414.   Hänninen and Salo, 1994,  Icarus 108, 325.   Hänninen and Salo, 1995,  Icarus 117, 435.    Ortiz et al. 2017, Nature 550, 219.   Salo, 1995, Icarus 117, 287.   Salo et al. 2018, in Planetary Ring Systems (Tiscareno and Murray, eds.), 434.   Sicardy et al. 2019, Nature Astronomy 3, 146.