SB10
Session assets
Please decide on your access
Please use the buttons below to download the presentation materials or to visit the external website where the presentation is linked. Regarding the external link, please note that Copernicus Meetings cannot accept any liability for the content and the website you will visit.
Forward to presentation link
You are going to open an external link to the presentation as indicated by the authors. Copernicus Meetings cannot accept any liability for the content and the website you will visit.
We are sorry, but presentations are only available for users who registered for the conference. Thank you.
Oral and Poster presentations and abstracts
We have performed numerical simulations of narrow rings around small bodies, addressing both the m=2 resonance perturbations induced by a rotating tri-axial ellipsoidal central body and the m=1 perturbations due to a mass anomaly on the surface of the central body. The simulations include up to 1e5 mutually colliding particles, and their partially inelastic impacts are resolved with the soft-sphere treatment introduced in Salo (1995; for details see Salo et al. 2018). An azimuthally complete ring is followed, and the integrations are performed in an inertial center-of-mass frame, lasting up to 1e5 central body rotations. Our goal is to see under which conditions the perturbation may prevent the collision-induced viscous spreading of the ring, instead leading to a confinement.
Our study is motivated by the narrow dense rings discovered around the tri-axial Centaur object Chariklo (Braga-Ribas et al. 2014) and the dwarf planet Haumea (Ortiz et al. 2017). In particular the Chariklo ring consists of two narrow components, with the inner ring having an optical depth of the order of unity and possessing sharp edges. While the ellipticity of the ring is poorly constrained (measurements are consistent with a circular ring), it is known to exhibit substantial width variations (Berard et al. AJ, 154, 144). Both Chariklo and Haumea rings are close to a distance where the orbital period equals three central body rotations, corresponding to a 2/6 resonance with a rotating ellipsoidal body, and a 1/3 resonance for a mass anomaly (Sicardy et al. 2019).
Sicardy et al. (2019) demonstrated that torques connected to resonances lead to a rapid clearing of particles from the vicinity of the central body, up to distances where orbital period equals two central body rotation periods. Their test particle calculations approximated the effects of impacts with an additional Stokes friction term. Our realistic collisional simulations confirm these results, and also indicate that the m=2 perturbation by the ellipsoidal body has an insignificant effect at the 2/6 resonance. On the other hand, we find that a sufficiently strong mass anomaly may eventually lead to formation of a narrow confined ring near 1/3 (Fig. 1).
What maintains the ring confined? Our favored mechanism is the reversal of angular momentum flux. Without perturbation, the outward flow of angular momentum, together with collisional dissipation, always implies radial dispersal of a narrow ring. However, in a strongly perturbed ring (say with an eccentricity gradient related to width variations) the direction of flux may reverse, leading to a confinement of sharp edges (Borderies et al. 1982). In Hänninen and Salo (1994, 1995; see also Goldreich et al 1995) such a confinement was verified in direct simulations of first order satellite Lindblad resonances, including the inner 2/1 (ILR) and outer 1/2 (OLR). Moreover, the
simulation-measured pressure tensor was shown to be in accordance with the theoretical mechanism. With the current code we have verified this early simulation result, and extended similar measurements to the 1/3 case. However, the 1/3 behaviour is more complicated due to the different order of the resonance. While in the ILR and OLR resonances the response of the ring is more or less steady in the frame rotating with the perturber, this is not so in the 1/3 case.
We are currently investigating in detail the confinement/ flux reversal mechanism, which results will be reported. We will also discuss the scaling between the simulated particle size and the magnitude of the mass anomaly required for confinement. Eventually, in order to extend the calculations to realistic particle sizes, a larger number of particles needs to be simulated in a multi-processor environment: for that purpose we plan to use the new REBOUND-based soft-sphere code recently applied to local simulations of viscous overstability (Mondino-Llermanos and Salo, this meeting; submitted to MNRAS). The soft-sphere impact treatment is important as the ringlets have a large optical depth; it will also facilitate the later inclusion of ring self-gravity, important for rings near the Roche zone where temporary clumping of particles is expected.
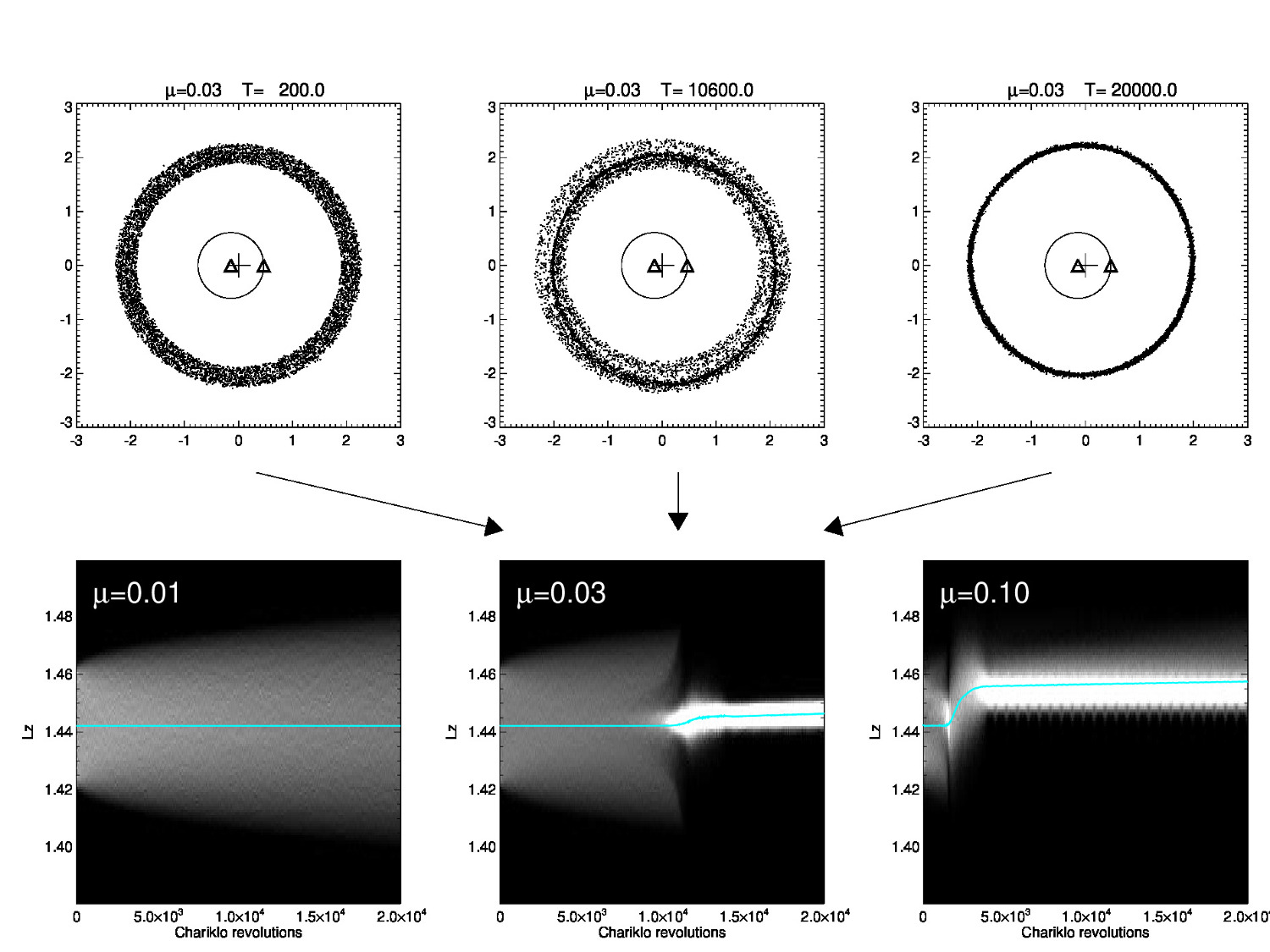
Figure 1.
Upper row: evolution of a ring around a spherical central body with a mass anomaly μ=0.03. Three snapshots of the ring are shown: the title indicates the time in terms of central body rotations. The ring is initially centered at the 1/3 resonance (2.08 times the corotation distance) and the size of the simulated particles corresponds to about 200 meters when scaled to the Chariklo system. In the plot the radial deviations from the resonance distance are exaggerated by a factor of three. Triangles indicate the locations of the central body and the mass anomaly, while the cross indicates the center-of-mass: for clarity, the deviations are exaggerated by a factor of 10.
Lower row: evolution of the distribution and mean value of angular momentum Lz, in three simulations with different μ. With μ=0.01 the perturbation is too weak to prevent the collisional spreading of the ring. With μ=0.03 (same simulation as in the upper row) and μ=0.1 the particle orbits gradually get organized in the vicinity of the resonance and eventually experience a rapid excitement of eccentricities accompanied by an outward drift in Lz. After resonance passage the eccentricities are damped and the particles form a narrow ringlet with confined sharp edges.
References:
Berard et al. 2017, AJ 154, 144. Borderies et al. 1982, Nature 299, 209. Braga-Ribas et al. 2014, Nature 508, 72. Goldreich et al., 1995, Icarus 118, 414. Hänninen and Salo, 1994, Icarus 108, 325. Hänninen and Salo, 1995, Icarus 117, 435. Ortiz et al. 2017, Nature 550, 219. Salo, 1995, Icarus 117, 287. Salo et al. 2018, in Planetary Ring Systems (Tiscareno and Murray, eds.), 434. Sicardy et al. 2019, Nature Astronomy 3, 146.
How to cite: Salo, H., Sicardy, B., Mondino-Llermanos, A., Soumi, D., Renner, S., Morgado, B., Braga-Ribas, F., Benedetti-Rossi, G., and de Santana, T.: Resonance confinement of collisional particle rings, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-338, https://doi.org/10.5194/epsc2021-338, 2021.
Narrow and dense rings have been discovered around the small Centaur object Chariklo (Braga-Ribas et al 2014) and the dwarf planet Haumea (Ortiz et al. 2017). Both ring systems are observed close to the 1/3 resonance with the central body, meaning that the particles complete one revolution while the body completes three rotations.
The potential of small bodies can have large non-axisymmetric terms when compared to the giants planets. As a result, strong resonant couplings occur between the body and a surrounding collisional, dissipative disk (Sicardy et al. 2019). Those resonances are described by a critical angle φ= mλ' - (m-j)λ - jϖ, where j>0 is the resonant order (i.e. the order in eccentricity of the resonant term in the Hamiltonian), m (m<0 or m>0) is the azimuthal number, λ' (resp. λ) is the rotational angle of the body (resp. the particle), and ϖ is the longitude of periapse of the particle.
Among the j= 1 (Lindblad), 2, 3 and 4 resonances, only the cases j= 1 and 2 can have an unstable (more precisely non-elliptic) point at the origin of the phase portrait describing [X= e.cos(φ), Y= e.sin(φ)], where e is the eccentricity and φ is the critical angle previously defined. The 1/3 resonant in particular has m=-1 and j=2, and is thus of second order. For a narrow range of the Jacobi constant associated with that resonance [i.e. a - (3/2)a0e2, where a is the ring's semi-major axis and a0 is the semi-major axis at exact resonance], the origin of the phase portrait is hyperbolic, hence unstable.
This instability triggers an eccentricity excitation of the ring near the 1/3 resonance, a source of torque on that ring. Such resonance can be created by a mass anomaly in the central body. We have tested this mechanism by simulating a ring with 30,000 particles undergoing inelastic collisions near the 1/3 resonance with Chariklo, in the presence of a large mass anomaly that represents 0.1 the mass of the body.
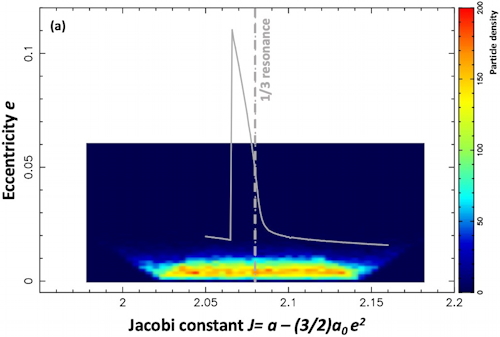
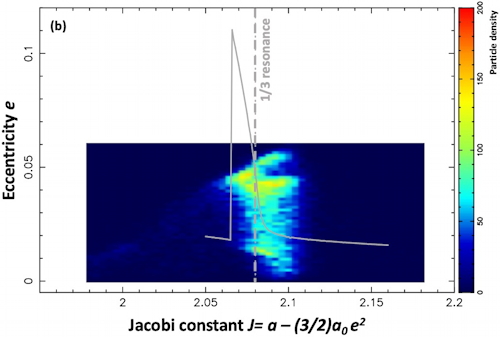
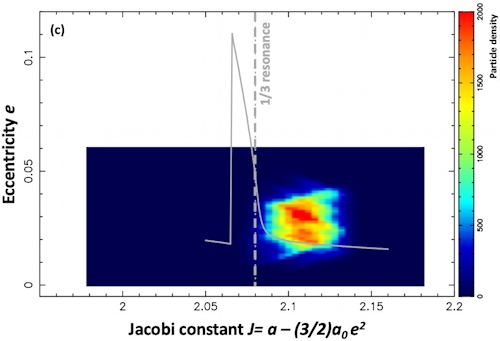
Preliminary results are shown in the figure above. The density of particles has been plotted in a (Jacobi constant-eccentricity) diagram, with the exact resonance location plotted as the vertical dash-dotted gray line. The solid gray line is the expected maximum eccentricity reached by particles for the corresponding Jacobi constant. Panel (a): initial conditions for the 30,000 ring particles; panel (b): the particles after 2,000 Chariklo rotations (about 1.6 years) during the excitation phase due to the 1/3 resonance; panel (c): the particles in the time interval 9,000-9,900 Chariklo rotations (~7-8 years). At that point, the ring has settled just outside the resonance location, reaching a balance between the eccentricity and semi-major dampings due to inelastic collisions, and the eccentricity excitation caused by the resonance.
More quantitative results will be presented, in particular the effect of smaller, more realistic, mass anomalies, and the assessment of a possible slow outward drift caused by a residual secular torque on the ring. Meanwhile, the observed behavior in those simulations appears as a promising mechanism to explain the proximity of both Chariklo's and Haumea's rings to the 1/3 resonance.
References
Braga-Ribas et al. 2014, Nature 508, 72
Ortiz et al. 2017, Nature 550, 219
Sicardy et al. 2019, Nature Astronomy 3, 146
Sicardy et al. 2020, in The Trans-Neptunian Solar System (Eds. D. Prialnik, M.A. Barucci and L. Young), Elsevier (Chapter 11)
Acknowledgements. The work leading to these results has received funding from the European Research Council under the European Community's H2020 2014-2021 ERC Grant Agreement n°669416 "Lucky Star".
How to cite: Sicardy, B., Salo, H., Souami, D., Renner, S., Morgado, B., Braga-Ribas, F., Benedetti-Rossi, G., and de Santana, T.: Rings around small bodies: the 1/3 resonance is key, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-91, https://doi.org/10.5194/epsc2021-91, 2021.
1. Introduction
After more than a dozen years in orbit about Saturn, the Cassini mission provided key measurements that are important for determining the age of Saturn’s rings. These include the extrinsic micrometeoroid flux at Saturn [1], the volume fraction of non-icy pollutants in the rings [e.g., 2], and the total ring mass [3]. These factors help to constrain the ring age to be no more than a few 100 Myr [1]. The Cassini Grand Finale also provided a suite of observations that demonstrate that the rings are losing mass to the planet at a surprising rate. Some of the mass flux falls as “ring rain” at higher latitudes consistent with the H+3 infrared emission pattern thought to be produced by an influx of charged water products from the rings [e.g., 4]. The contribution needed to account for the ring rain phenomenon though is considerably less than the total equatorial measured mass influx of 4800 – 45000 kg/s [5]. Taken together, these observations imply that the rings are not only young, but also ephemeral. Here we argue that bombardment by micrometeoroids can account for these observations.
2. What’s Driving the Mass Inflow?
It has been recently argued that the above age estimate for the rings derived from exposure to micrometeoroids is not the same as their formation age, and that the rings could look young but still be quite old [6]. At their current mass, the observed mass inflow is orders of magnitude more than what viscous evolution can currently produce [7,8]. However, recall that micrometeoroid bombardment (MB) not only leads to pollution of the rings over time (as well as a catalyst for ring rain), but also to exchange of mass and angular momentum throughout the rings due to ballistic transport (BT) of their impact ejecta. As a result of this fundamental feature of BT, the rings act like an accretion disk with outward angular momentum transport leading to a steady inward drift of material to the planet. In [8], we quantify this radial drift rate in the context of a quasi-steady uniform ring using an accretion disk analog to show that for plausible choices of the ejecta yield Y , that direct deposition (mass loading, ML) of micrometeoroids and BT can produce the observed mass inflow rates (Fig. 1). More importantly it means that as ring mass decreases and viscosity can no longer effectively drive their evolution, the rings can continue to dynamically evolve driven by MB. This has implications not only for the formation age and initial mass of Saturn’s current rings, but also for the long-term evolutionary state of planetary rings.
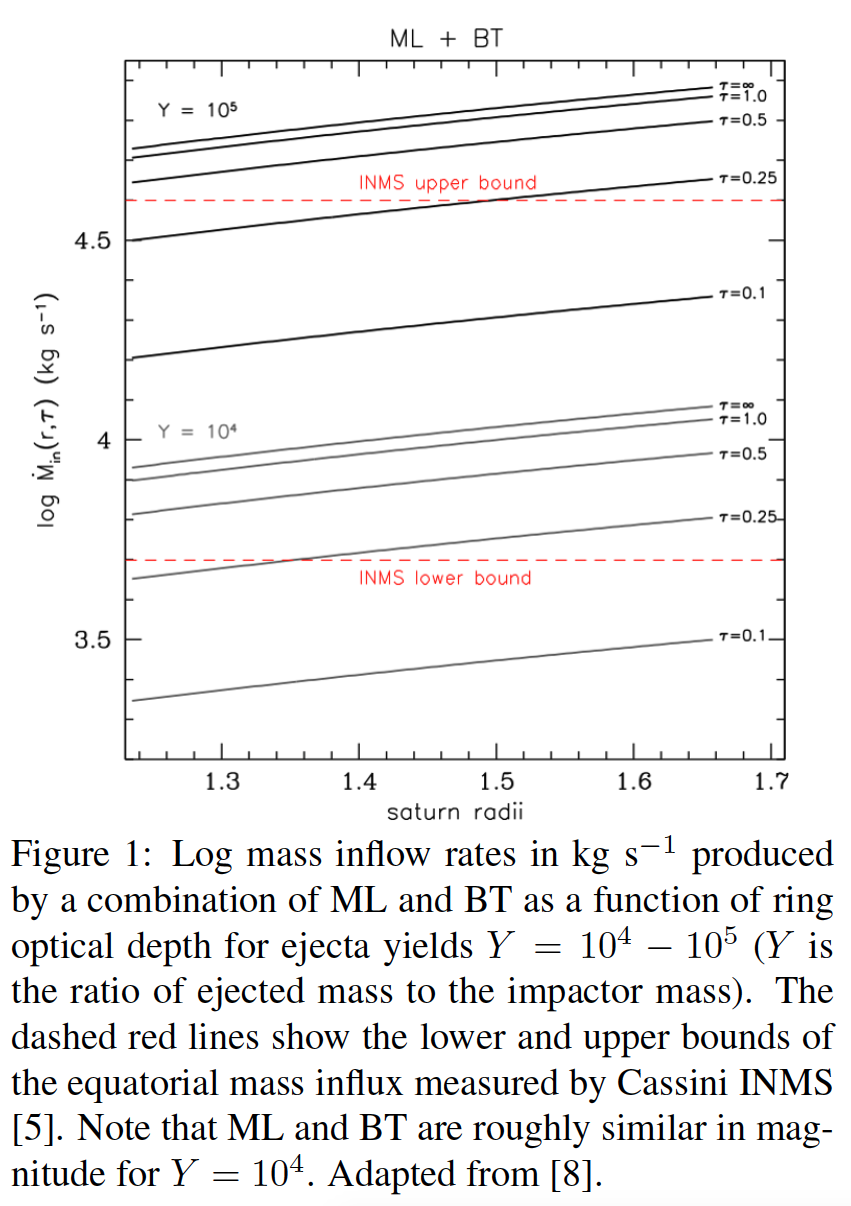
3. Evolution Under ML & BT
In [9] we have modeled the dynamical evolution of rings with initial disk masses ranging from 1-100 Mimas under the effects of viscosity and ML (Fig. 2, upper panel). For comparison, we show (blue dashed curve) the evolution due to viscosity alone for an initial disk mass of 100 Mimas [see 7]. This occurs because the evolution of massive rings is driven very strongly early on by viscosity, but weakens at later times as the ring spreads. We find though that when we include just ML (black curves), the rings’ dynamical evolution is eventually driven more strongly by ML once a threshold mass is achieved, and the ring mass continues to decrease. This result suggests, based on ML alone, that a primordial massive ring would likely have become low mass much earlier on in Solar System history, especially if the flux was much higher in the past. If one also includes BT (shown for 1 Mimas mass, magenta dotted curve) with Y = 104 for comparison, evolution (and mass loss) is greatly accelerated leading to much shorter life times. Figure 2 (bottom) shows the corresponding pollution rates which all achieve the observed range of volume fractions (green dotted lines) of non-icy material in the A/B rings [3] in ≤ few 100 Myr timescales independent of initial mass.
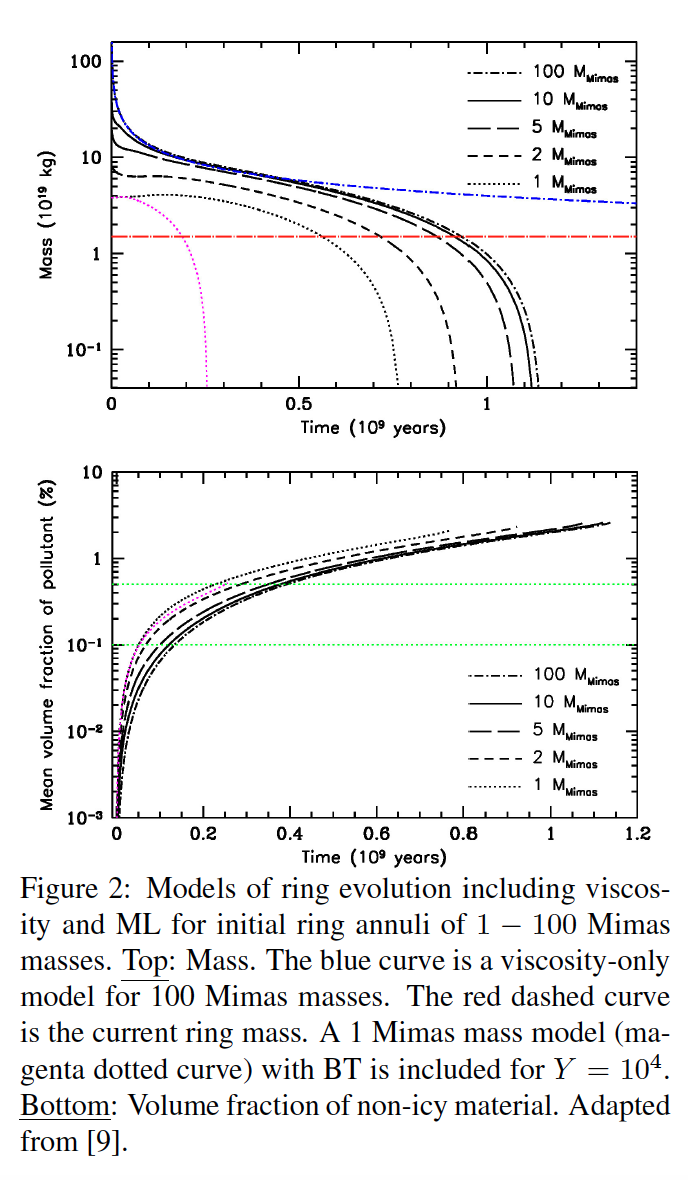
4. Implications for Ring Evolution
These results suggest that if the micrometeoroid flux was relatively constant at least at its current measured value [1] then the rings cannot be ancient, regardless of their initial mass. Moreover, given the relatively short life time of rings subject to the effects of MB, it is highly unlikely then that they started so massive, so recently. We argue in [9] using lower initial mass evolutionary models that the rings appear consistent with being only ∼100 Myr old, and likely had an initial mass of ∼1-4 Mimas masses with a remaining lifetime of ≤200 Myr. In these models, we have ignored that BT manifests and plays an important role in structural evolution which imposes additional constraints strengthening this argument. Such complicated effects require more detailed models which is the subject of ooing work. In reality, we expect that rings will achieve such low mass that BT becomes inefficient at further transport, and speculate that even initially massive rings will evolve to a highly polluted, low density tenuous state similar to the rings of Uranus and Neptune. This would be in agreement with Crida and Charnoz [10] who first suggested these ice giants may have had initially massive rings.
Acknowledgements: This work was supported by a grant from NASA’s Cassini Data Analysis Program.
References:
[1] Kempf, S., et al.: In prep., 2021
[2] Zhang, Z., et al.: Icarus 294, 14-42. 2017
[3] Iess, L., et al.: Science 364, id.aat2965, 2019
[4] O’Donoghue, J., et al.: Icarus 322, 251-260, 2019
[5] Waite, J. H., et al.: Science 362, id.aat2382, 2018
[6] Crida, A. et al.: Nature Astronomy 3, 967-970, 2019
[7] Salmon, J. et al.: Icarus 209, 771-785, 2010
[8] Durisen, R. H. & Estrada, P. R.: Icarus, sub., 2021
[9] Estrada, P. R., & Durisen, R. H.: Icarus, sub., 2021
[10] Crida, A. & Charnoz, S.: Science 338, 1196, 2012
How to cite: Estrada, P. and Durisen, R. H.: Diamonds are Not Forever: Dynamical Evolution of Saturn’sRings Driven by Micrometeoroid Bombardment, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-869, https://doi.org/10.5194/epsc2021-869, 2021.
Saturn's rings are well known for many good reasons, one of them being their brightness. Made of almost 99% water ice, they are by far the most ice-rich object of the solar system, and their composition is still a puzzle. Most formation models rely on the stripping of the icy mantle of a large body, be it by colision with a comet or tidal disruption of a passing centaur or a migrating satellite, providing the rings with an initial pure water composition. However, the rings are constantly bombarded by micrometeorites, which are made of at least half non icy material (hereafter "dust"). Based on the percentage of dust in the rings (Zhang et al. 2017a,b), the mass of the rings (Iess et al. 2019), and estimates of the bombardment rate, an exposure age of 10 to 100 million years has been derived. This age is simply the time it would take to bring all the dust observed in the rings through a constant bombardment at the present rate, assuming the rings are initially devoid of dust and keep all the pollution they recieve. It had been initially interpreted as the physical age of the rings (as illustrated by Figure 1). Crida et al. (2019) have shown that the exposure age and the formation age are actually two different concepts and could differ. This claim is supported by the results by Hsu et al. (2018) and Waite et al. (2018) who have found that the rings lose non icy material into Saturn ; this suggests the existence of some unknown but non-negligible cleaning mechanism.
Here, we explore the possibility of a cleaning mechanism in the rings, and perform numerical simulations and analytical calculations of the evolution of the pollution rate in the rings for various scenarios. When the cleaning is modeled by a characteristic time τc such that the time derivative of the dust density d is -d/τc , an equilibrium dust profile exists, and the dust fraction doesn't grow linearly with time. In fact, if the initial composition of the rings is more dust-rich than the equilibrium profile, the dust fraction then decreases with time to converge towards this equilibrium. Such a (yet unknown) cleaning mechanism would open the possibility for initially non-pure ice rings, if the cleaning time is shorter than the age of the solar system.
More interestingly, the equilibrium profile is similar to the one obtained without cleaning but for a ring age of τc . In other words, there is no way of deciding whether the exposure age represents the real age of the rings or their cleaning time, as illustrated by how similar the figures 1 and 2 are. We find parameters that allow to reproduce the present rings density and pollution after 4.5 Gyr of evolution (figure 2). This shows that old rings are still a valid possiblity, and that the theory of their cleaning desserves further investigation.
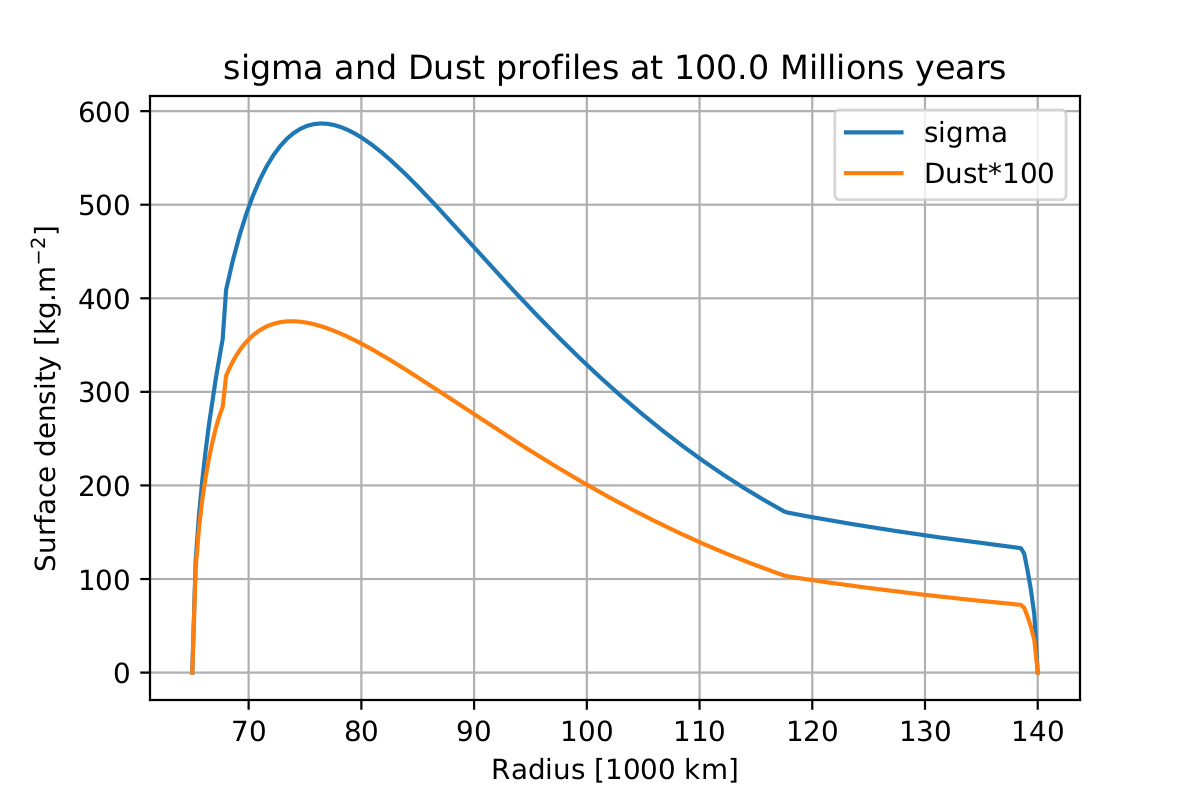
Figure 1 : Ring density profile (blue) and dust density profile (orange) after 100 Myrs of viscous evolution with a meteoritic bombardement following the parameters used by Zhang et al. (2017a), starting with a density profile equal to the one shown in figure 2, but with zero dust. No cleaning is used in this simulation. The result is similar to the actual A and B rings, showing that they correspond to 100 Myrs exposure age.
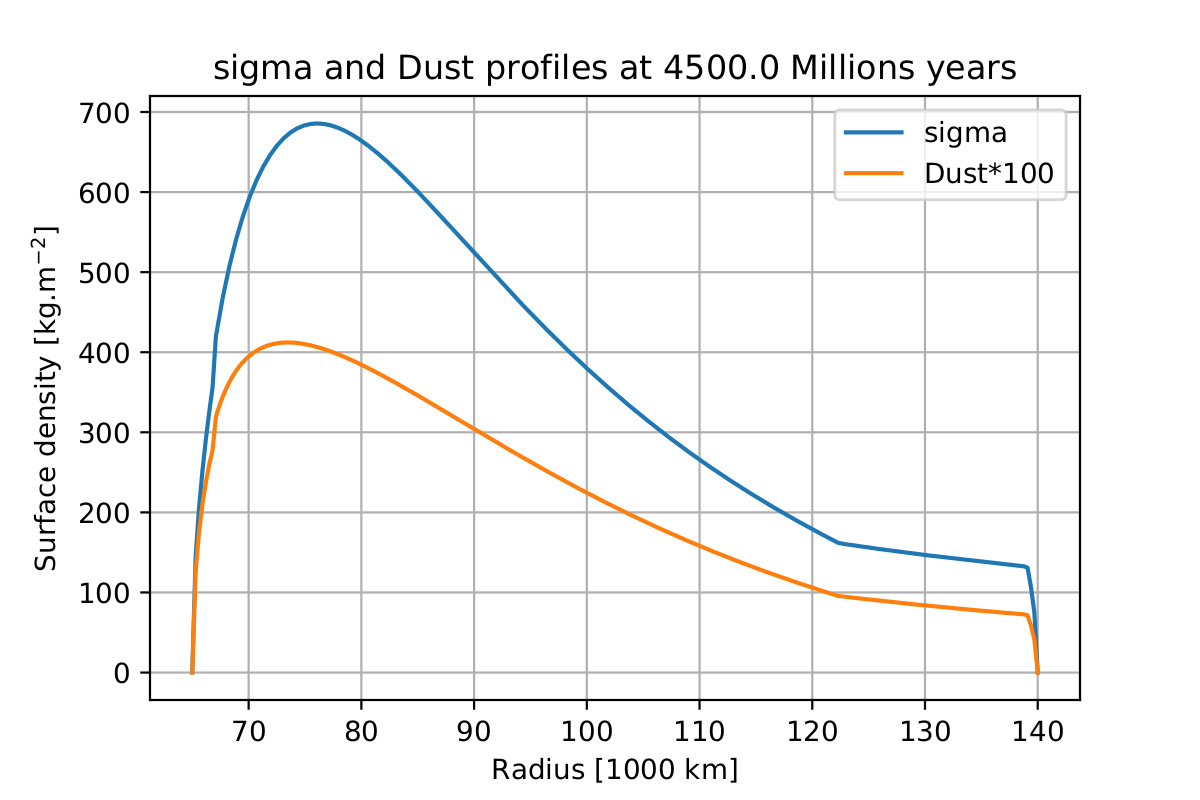
Figure 2 : Ring density profile (blue) and dust density profile (orange) after 4.5 Gyrs of viscous evolution reproducing Salmon et al. (2010), with a meteoritic bombardement following the parameters used by Zhang et al. (2017a) and a cleaning time τc = 100 Myrs. The result is almost identical to the one of Figure 1, and doesn't depend on the initial dust content of the rings, showing that an efficient cleaning mechanism can reconcile old rings with their apparent youth.
References:
Crida A., Charnoz S., Hsu H.-W., Dones L. (2019) Are Saturn's rings actually young ? Nature Astronomy 876, 437
Hsu H.-W. et al. (2018) In situ collection of dust grains falling from Saturn’s rings into its atmosphere. Science 362, eaat3185
Iess L. et al. (2019) Measurement and implications of Saturn’s gravity field and ring mass. Science 364, eaat2965
Salmon J., Charnoz S., Crida A., Brahic A. (2010) Long-term and large-scale viscous evolution of dense planetary rings Icarus 209,771-785
Waite J. R. et al. (2018) Chemical interactions between Saturn’s atmosphere and its rings. Science 362, eaat2382
Zhang, Z. et al. (2017) Exposure age of Saturn’s A and B rings, and the Cassini Division as suggested by their non-icy material content. Icarus 294, 14–42
Zhang, Z. et al. (2017) Cassini microwave observations provide clues to the origin of Saturn’s C ring. Icarus 281, 297–321.
How to cite: Crida, A. and Bramardi, G.: Effects of cleaning in Saturn's rings, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-393, https://doi.org/10.5194/epsc2021-393, 2021.
During the final mission phase, the Cassini spacecraft travelled through the gap between Saturn and its innermost D ring. One goal of these highly inclined orbits was sampling the dust population, mostly made of impact ejecta from the main rings, in the vicinity of the planet. These in situ measurements were primarily carried out by the Cosmic Dust Analyzer (CDA) onboard the spacecraft, which provided time-of-flight mass spectra of individual ice and dust grains, mostly between about 10 and 50 nm in size. Here we present an update on the composition of the silicate dust fraction stemming from Saturn’s main rings, which makes up about 30 % of the observed particles with water ice being the remaining fraction [1].
Elemental analysis of the silicate spectra was performed using an updated deconvolution method, based on a technique originally applied to the interpretation of CDA interstellar dust measurements [2]. Neighboring spectral peaks due to mineral-forming ions such as Mg+, Al+ and Si+ are often unresolvable, because of CDA’s relatively low (m/dm = 20–50) mass resolution [3]. Therefore, application of a deconvolution technique is required to disentangle the peak interferences and derive valuable compositional information. The robustness of the applied method has been tested and optimized through comparison with an independent automated fit algorithm. In order to calculate elemental abundances within the particles, the derived ion abundances were combined with experimentally-determined relative sensitivity factors (RSFs) [4]. To provide context to the measured element ratios, we compared them with a variety of space-relevant materials. We find an overlap with chondritic material for Mg/Si and Fe/Mg ratios. The observed range within the element ratios, however, indicates the contribution of a variety of minerals such as olivine, plagioclase or pyroxenes. Although our results agree with realistic mineral compositions, the calculated abundances of Al+ ions are still relatively uncertain and can be seen as an upper limit.
Additionally, we present the results of a dynamical model, which allow us to derive the likely source region within the main rings of individually detected silicate grains. We find the C and B rings to be the most likely sources of the vast majority of grains with the D ring being only a minor source. Currently an analysis of compositional diversity between the different ring segments is under way.
References
[1] H.-W. Hsu et al. (2018) In situ collection of dust grains falling from Saturn’s rings into its atmosphere. Science 362.
[2] N. Altobelli et al. (2016) Flux and composition of interstellar dust at Saturn from Cassini’s Cosmic Dust Analyzer. Science 352, 312–318.
[3] R. Srama et al. (2004) The Cassini Cosmic Dust Analyzer. Space Science Reviews 114, 465–518.
[4] K. Fiege et al. (2014) Calibration of relative sensitivity factors for impact ionization detectors with high-velocity silicate microparticles. Icarus 241, 336–345.
How to cite: Linti, S., Hillier, J., Fischer, C., Hsu, H.-W., Trieloff, M., and Postberg, F.: Compositional in situ analysis of dusty material stemming from Saturn’s main rings, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-181, https://doi.org/10.5194/epsc2021-181, 2021.
Abstract
Mass spectra from the Cosmic Dust Analyzer (CDA) [1] onboard the Cassini spacecraft revealed the existence of different compositional types of icy dust particles in Saturn’s E-ring. Most of these µm to sub-µm water ice grains were ejected from the cryo-volcanoes at the southern polar region of Enceladus and carry different constituents, for example organic compounds or salts [2-5]. These particles are subject to ongoing plasma sputtering during their lifetime in the E-ring [6,7].
Recent modelling of the dynamics of E-ring particles has shown that, in the region between the orbital distances of Dione and Rhea, the outwards migration of a proportion of the E-ring dust slows down and almost comes to a halt [8]. Due to the minimum of the V-shaped electrostatic grain equilibrium potential [9] and a polarity reversal of the dust surface charges [10], the semi-major axes of the dust particles’ orbits actually stop growing, forcing the particles to spend a significant part of their lifetime at this distance from Saturn. Therefore, this phenomenon should allow plasma sputtering to operate much longer on the dust particles residing in this region, potentially resulting in detectable alterations to the dust particle properties, e.g. particle composition and size, in this region.
Here we present the discovery of a new population of grains within the E ring, which show signs of compositional alteration, best explained by plasma sputtering. The radial frequency distribution of these grains shows a distinct accumulation in the region between the orbits of Dione and Rhea, and may provide evidence of prolonged residence there. Analyses of CDA mass spectra of the grains, interpreted via comparison with laboratory Laser‐Induced Liquid Beam Ion Desorption (LILBID) [11] analogue experiments, indicate the particles to be very salt-rich water ice. In comparison to the previously reported salt-rich particle types, generated from Enceladus’ subsurface ocean [3,4] this new population must possess a far higher salt concentration to explain its observed spectral appearance. We propose that the increase in salt concentration arises from sputtering-induced removal of water from less salty oceanic grains (Type 3) [3,4], during their extended time in the region between Dione and Rhea. This population may therefore represent the first confirmation of the proposed dynamical barrier within Saturn’s E-ring.
References
[1] Srama, R. et al., The Cassini Cosmic Dust Analyzer, Space Science Reviews, 114, 465-518, 2004.
[2] Hillier, J. et al., The composition of Saturn’s E ring, Mon. Not. R. Astron. Soc., 377, 1588–1596, 2007
[3] Postberg, F. et al., The E-ring in the vicinity of Enceladus II. Probing the moon’s interior-The composition of E-ring particles, Icarus, 193, 438-454, 2008.
[4] Postberg, F. et al., Sodium salts in E-ring ice grains from an ocean below the surface of Enceladus, Nature, 459, 1098-1101, 2009.
[5] Postberg, F. et al., A salt-water reservoir as the source of a compositionally stratified plume on Enceladus, Nature, 474, 620–622, 2011
[6] Jurac, S. et al., Saturn’s E Ring and Production of the Neutral Torus, Icarus, 149, 384–396, 2001
[7] Johnson, R. E. et al., Sputtering of ice grains and icy satellites in Saturn’s inner magnetosphere, Planetary and Space Science, 56, 1238–1243, 2008
[8] Kempf & Beckmann, Dynamics and long-term evolution of Saturn's E ring particles (in prep.)
[9] Mitchell, C. J. et al., Tenuous ring formation by the capture of interplanetary dust at Saturn, JOURNAL OF GEOPHYSICAL RESEARCH, 110, 2005
[10] Kempf, S. et al., The electrostatic potential of E ring particles, Planetary and Space Science, 54, 999-1006, 2006
[11] Klenner, F. et al., Analogue spectra for impact ionization mass spectra of water ice grains obtained at different impact speeds in space, Rapid Commun Mass Spectrom., 33, 1751–1760, 2019
How to cite: Nölle, L., Postberg, F., Kempf, S., Hillier, J., Khawaja, N., Klenner, F., Hsu, S., and Srama, R.: Compositional Indicators for a Dynamical Barrier within Saturn’s E-ring, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-146, https://doi.org/10.5194/epsc2021-146, 2021.
Introduction
We show how Saturn could create rings with the additional action of its magnetic field. Our model of the Saturn's rings origin includes the appearance of additional third force of diamagnetic expulsion of ice particle after emergence of axisymmetric Saturn’s magnetic field and mechanism of magnetic anisotropic accretion. This force of diamagnetic expulsion is acting together with force of gravity and centrifugal one on the particles within protoplanetary cloud. Cassini found 93% of ice in the particles of rings. The rings could have originated from the ice particles moving under the influence of centrifugal force and force of gravity in chaotic orbits around Saturn within protoplanetary cloud after the planet's magnetic field was emerged. After appearing of the force of diamagnetic expulsion of ice particles, all their chaotic orbits start shifting to the magnetic equator plane, where the minimum of magnetic energy of the particles is observed. Every particle on the magnetic equator comes to a stable position, and it prevents its horizontal and vertical shift. The particles are trapped within three-dimensional magnetic well and they form rings structure. Our model doesn't refute earlier theories, but rather improves them and explains many of the observed phenomena in rings.
The origin of Saturn's rings by taking into account the diamagnetism of ice particles and the mechanism of magnetic anisotropic accretion
We follow our paper V. V. Tchernyi, S.V. Kapranov, arxiv.org/abs/2104.03967, May 17, 2021. The problem of the origin of Saturn's rings has no definitive answer. Existing theories are based upon gravitational defragmentation of massive body approached Saturn or comet tidal disruption (A.I. Tsygan, SovA, 1977; A.M. Fridman, N.N. Gorkavyi, UFN, 1990; S. Charnoz et al, Icarus, 2009; R. M. Canup, Nature, 2010). These scenarios do not explain well how it turns out that the disk of sombrero rings is well constructed with separated particles, their fine structure, etc. The role of Saturn’s magnetic field is unclear. Once compare the ratio of the thickness of the rings to their diameter with the ratio of the thickness of the paper sheet to its length, the relative thickness of the disc of the rings is a thousand times less. It is a challenge that a thin film of ice particles of a huge diameter hangs in outer space. This is an emphasis on the important role of all interactions in the origin of rings, especially those that have not yet been described. It was experimentally determine the ice of the Saturn rings is like ice on the Earth (R. Clark al, Icarus, 2019, 322). Then the ice XI has stable parameters at the temperature of the rings and it is diamagnetic (R.J. Hemley, ARPC, 51, 2000). Our model assumes that after the appearance of Saturn's magnetic field and the force of diamagnetic expulsion of ice particles, the chaotic orbits of all the particles inside the protoplanetary cloud began to shift to the magnetic equator plane and finally formed a system of rings. We call this process magnetic anisotropic accretion due to the axisymmetric magnetic field of Saturn. The gravitational force in the orbit of the particle is balanced by the centrifugal force and the force of diamagnetic expulsion.
We need to demonstrate how protoplanetary cloud can collapse into a disk of rings (Fig. 1).
a b c
Fig. 1. Transformation of Saturn's protoplanetary cloud into a disk of rings after appearance of Saturn’s magnetic field and interaction of it with the iced particles: from (a) >> (b) >> to (c)
We use concept of V. Safronov: Evolution of the protoplanetary cloud and formation of Earth and planets, NASA, 1972. The mathematical solution of our problem is based on the work of V. Cherny and S. Kapranov (ApJ, 2020, May 6, 894, 1). First, we solve the problem of a single diamagnetic spherical particle located in the external gravitational field and magnetic field of Saturn. The equation for the azimuthal angle of the particles is:
We see all orbits of ice particles at the end of their movement entering to magnetic equator plane. The solution ϴ = π/2 accounts for essentially planar structure of Saturn’s rings and their location in the magnetic equator plane. The equation for azimuthal velocity of particles is:
We see the gravity force in the particle’s orbit is counterbalanced by both the centrifugal force and the force of diamagnetic expulsion.
Conclusions
It follows from our solution, in the superposition of the spherically symmetric gravitational field and axially symmetric magnetic field, the orbits of particles finally fall on the magnetic equator plane and formatted rings structure of Saturn. It also explains the essentially planar structure of the rings. Density gradient flow of the magnetic field repels particles of each other and it also cleans the gaps within rings system and forms rigid thin structure of separated rings.
Each particle comes to the stable position at the magnetic equator of Saturn and preventing its own move up or down of it due to minimum magnetic energy at this position. The horizontal displacement of the particles is prevented by the inhomogenity of the magnetic field along the radius.
The force of diamagnetic expulsion from the disk-shaped structure is stronger, and the potential barrier at the magnetic equator is larger. This means high stability of the particles inside the sombrero rings.
The spokes in the B ring have clear explanation due to diamagnetism of the ice particles. The action of magnetic field on diamagnetic particles is stronger the smaller particles size. Small particles coming to the anomalous positions of the magnetic field of Saturn change their position, and we see it as spokes.
How to cite: Tchernyi (Cherny), V. and Kapranov, S.: How could Saturn form rings involving the third force of diamagnetic expulsion and the mechanism of magnetic anisotropic accretion, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-362, https://doi.org/10.5194/epsc2021-362, 2021.
Saturn's rings exhibit a phenomenal wealth of structures covering a vast range of length scales (Porco et al. 2005). On the sub-kilometer scale, various instruments aboard the Cassini mission revealed the presence of quasi-periodic radial density variations at several locations of Saturn’s B and inner-A ring, where optical depth ∼1–2 (Colwell et al. 2007; Thomson et al. 2007; Hedman et al. 2007). To date, axisymmetric viscous overstability offers the most plausible explanation for these short-scale axisymmetric structures.
The emergence of viscous overstability was directly demonstrated for the first time in fully self-gravitating 3D N-body simulations, once the optical depth τ≥1. Otherwise, in the absence of self-gravity no overstability was seen until τ∼4. Further analysis showed that the ring’s vertical self-gravity is crucial in promoting the overstable behaviour at optical depths close to unity (Salo et al. 2001).
So far, the theoretical understanding of overstable ring systems relies on analytical results based on approximate treatments of ring self-gravity that omit the emergence of self-gravity wakes. The interplay between these two mechanisms, self-gravity and overstability, is still not well understood. The above mentioned self-consistent numerical experiments in Salo et al. (2001) indicated that self-gravity wakes and overstable oscillations can coexist, although only if the self-gravity is not too strong. More recently, Ballouz et al. (2017) confirmed this and moreover demonstrated that overstability can tolerate substantially stronger self-gravity if friction and sticking forces between particles are included in simulations.
We present a systematic study on the onset of viscous overstability in self-gravitating dense rings, in which we address numerically the factors that determine its occurrence: optical depth, particle elasticity and gravity-related parameters rh and/or Ωz/Ω. For this purpose we use our novel adaptation of the open-access code REBOUND (Rein & Liu 2012). Our version uses soft-sphere particle collisions while retaining the originally implemented Barnes-Hut tree algorithm for a self-consistent calculation of particle-particle gravity. Some details concerning this new version of the source code are discussed, as it will be publicly released in the near future.
We find that weak self-gravity promotes overstability whereas strong self-gravity, with prominent wake structure, weakens the overstable pattern. This strong self-gravity regime corresponds to large optical depths at intermediate rh, or to moderate optical depths at high rh. While the dependence on rh is known from earlier simulations, the suppression at high optical depths is a new finding. Both cases are illustrated in Figures 1 and 2.
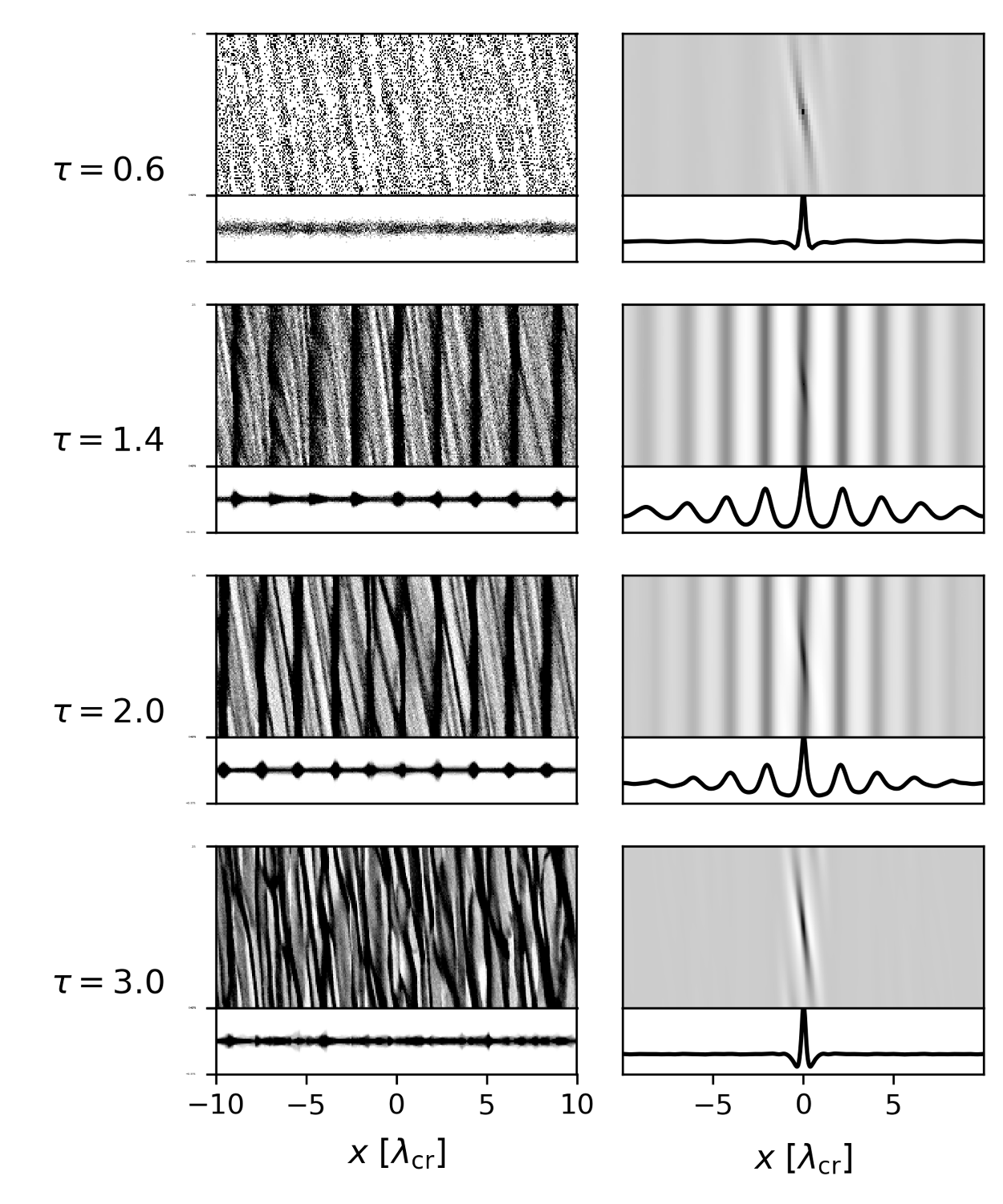
Figure 1. Self-gravitating local simulations with different optical depths, for fixed rh=0.61 and ε=0.1. The dimensions of the simulation box are 20λcr × 5λcr. Left column: Snapshot of the x-y (top) and x-z (bottom) particle distribution at 300 orbital periods. Notice that in the zx-projection the vertical scale is stretched by a factor 5. Right column: 2D autocorrelation function ζ2D(x,y) together with the corresponding 1D radial cut along the abscissa, averaged over 150–300 orbital periods. Grey scale extends from 0.9 to 1.4 times the mean value, while ζ2D(x,0) is displayed in the range 0.85–1.35.
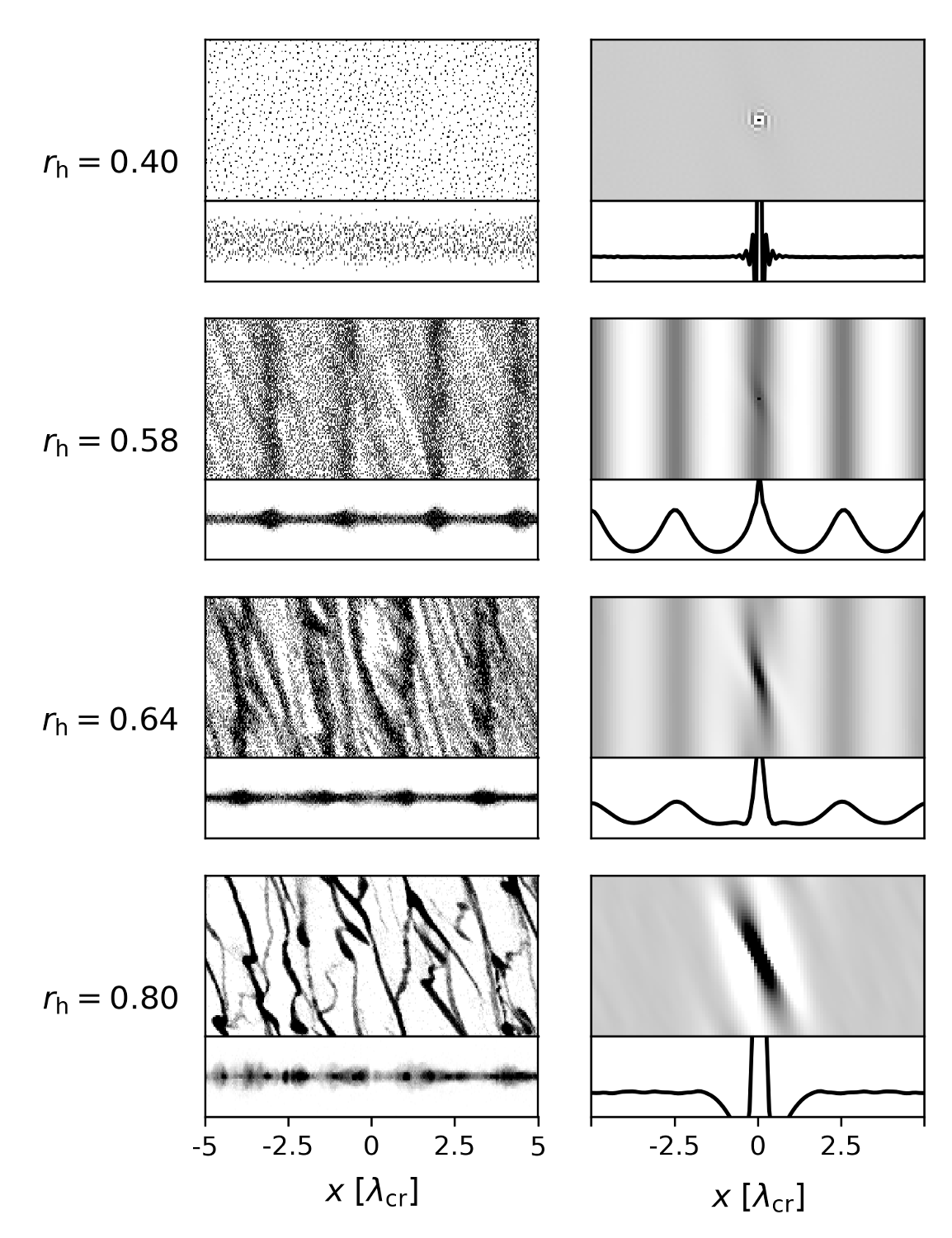
Figure 2. Self-gravitating local simulations with τ=1.0 and ε=0.1. The dimensions of the simulation box are 10λcr × 5λcr. Left column: Snapshot at 300 orbits. Note that the xz-projection the vertical scale is stretched by a factor of 3 compared to the radial. Right column: 2D autocorrelation function ζ2D(x,y) together with the corresponding 1D radial cut along the abscissa, averaged over 150–300 orbital periods. Grey scale and ζ2D(x,0) ranges are the same as in Figure 1.
To investigate the separate role of ring particles’ mutual self-gravity components in the promotion/suppression of viscous overstability we conduct a new type of hybrid experiments which combine a self-consistently calculated planar self-gravity with a separately adjusted vertical gravity field. Whereas in the case of fully self-consistent self-gravity the overstability is limited to rh=0.5–0.6, in hybrid method this regime can be extended using larger Ωz/Ω (see Figure 3); in this respect the method mimics the effects of including particle-particle surface forces done in Ballouz et al. (2017).
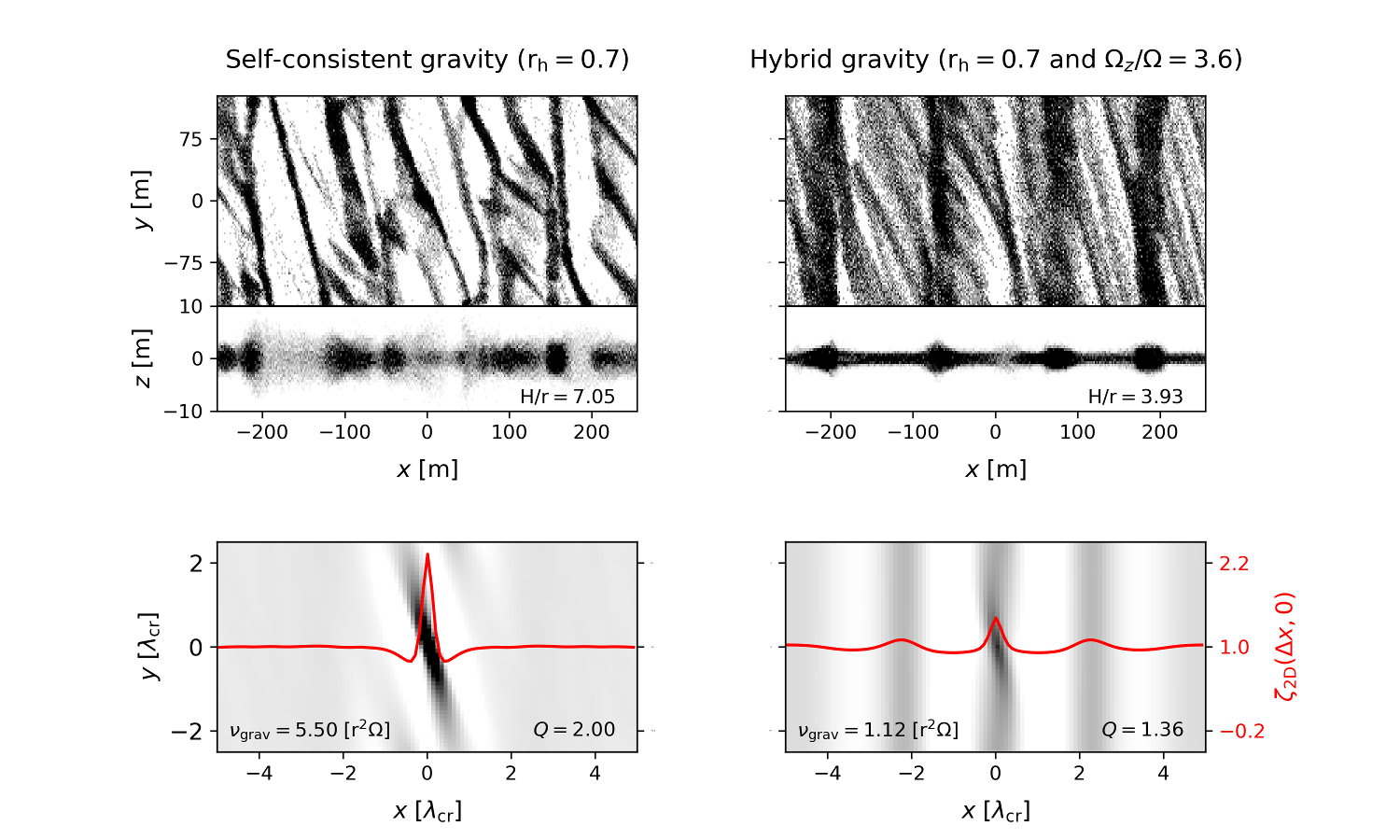
Figure 3. Comparative example between self-consistent (left) and hybrid (right) self-gravity simulations at rh=0.70 with τ=1.0 and ε=0.1. The vertical frequency enhancement use for hybrid method is Ωz/Ω=3.6. Some physical quantities like Toomre parameter Q (Toomre 1964), ring vertical thickness in terms of particle radius H/r, and the gravitational viscosity component νgrav are provided inside the panels. Top: Snapshot after 300 orbital periods. Bottom: 2D autocorrelation function averaged over 150–300 orbital periods together with the corresponding radial cut at y=0.
Finally, we derive a composite criterion for the onset of overstability valid even in the regime of strong gravity wakes and framed in terms of collective properties of the system: the central-plane filling factor and the ratio of gravitational and collisional viscosities. The combined semi-empirical condition reads:
FF(0) > FF(0)cr(rh) and νgrav / νcoll ≤ 0.3,
where FF(0)cr decreases monotonically when the strength of ring-plane self-gravity is increased, from ∼0.45 for the non-gravitating case to ∼0.3 at rh=0.76. In the limit where gravity wakes are omitted, this criterion agrees with that found by the kinetic theory analysis of the linear stability in Latter & Ogilvie (2008).
References:
Ballouz R.-L., Richardson D. C., Morishima R., 2017,AJ, 153, 146
Colwell J. E., Esposito L. W., Sremčević M., Stewart G. R., McClintockW. E., 2007,Icarus,190, 127
Hedman M. M., Nicholson P. D., Salo H., Wallis B. D., Buratti B. J., BainesK. H., Brown R. H., Clark R. N., 2007,AJ, 133, 2624
Latter H. N., Ogilvie G. I., 2008,Icarus,195, 725
Porco C. C., et al., 2005,Science,307, 1226
Rein H., Liu S. F., 2012,A&A,537, A128
Salo H., Schmidt J., Spahn F., 2001,Icarus,153, 295
Thomson F. S., Marouf E. A., Tyler G. L., French R. G., Rappoport N. J.,2007,Geophys. Res. Lett.,34, L24203
Toomre A., 1964,ApJ,139, 1217
How to cite: Mondino-Llermanos, A. and Salo, H.: Conditions for Axisymmetric Viscous Overstability in Self-gravitating rings, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-640, https://doi.org/10.5194/epsc2021-640, 2021.
The Cassini Ultraviolet Imaging Spectrograph (UVIS) High Speed Photometer (HSP) observed 15 occultation traces of the bright star Hadar (Beta Centauri) in 2008-2009 at an elevation above the ring plane of 66.7 degrees. The combination of the high signal from this star (up to 600 counts per msec integration period) and its high elevation above the rings means these occultations provide the strongest constraints on the transparency of high optical depth regions as observed by UVIS.
We use the excess variance that is introduced into the UVIS stellar occultation counting rates by the presence of ring particles to determine when the observed signal is purely background with no transmitted starlight. When the observed variance is equal to the mean, we identify the region as opaque. We have identified several regions that are opaque in the UVIS occultations in the B2 and B3 regions (Marouf et al. 2006). When comparing these regions between occultations of the same star, we discovered non-repeating, narrow regions where the transparency jumps from less than 1% up to as much as 20%. These regions are typically less than 100 m in radial extent and frequently less than 50 m. These regions do not repeat at the same location between occultations. In addition, we are able to take advantage of the fact that Hadar is a binary star and both components produce measurable signals in the HSP data. These partially transparent features produce two distinct signals in the occultation data if the azimuthal extent of the feature is at least as large as the projected separation of the two stars onto Saturn’s rings. In many cases we find that there is only one feature observed, indicating that the features are not only narrow in the radial direction but also of limited (< 100 m) extent in the azimuthal direction. We refer to these features as “phantoms” due to their similarity to the completely transparent regions identified in the C ring plateaus dubbed “ghosts” (Baillie et al. 2013).
Figure 1 shows an example of an opaque region in the B2 region of the B ring in all 15 occultations of Hadar. In all but two of the 15 profiles there is a narrow spike with a transparency of 5% up to nearly 20% in the region between 100,090 km and 100,130 km. If a transparent region is observed in all occultations at the same location, we identify that as a boundary between two opaque regions rather than as a phantom. The region between ~100,140 – 100,160 km in Figure 1 has complicated structure that is not exactly repeated between the occultations but marks the boundary between two opaque regions. The phantoms, observed between 100,090 km and 100,130 km, do not repeat and are generally very narrow. The first 15 km of the next opaque region, seen from 100,165-100,180 km in Figure 1 are virtually free of phantom features.
The projected separation of the two components of Hadar is less than 50 m in the azimuthal direction, and frequently phantoms are only seen to pass behind one of the two stars. The actual transparency of narrow phantoms is thus approximately twice as high as that shown in Figure 1, because the transparency is based on the combined brightness of the two components. Baillie et al. (2013) suggested that ghosts are the nearly empty openings in the background ring carved out by small moonlets akin to the propeller features imaged in the A ring. The situation may be similar for the phantoms, but the dynamics of neighboring ring particles resulting from embedded moonlets in the dense B ring may not produce the same orbital perturbations that give rise to propeller features. We will describe the distribution and characteristics of opaque regions and phantoms in the B2 and B3 regions.
Figure 1: Transparency of 100 km of the B2 region of Saturn’s B ring showing an opaque region extending from approximately 100084 km to 100140 km, and part of another beginning at about 100162 km. Each curve is offset by 5% for clarity.
Bibliography:
Baillié, K., J. E. Colwell, L. W. Esposito, and M. C. Lewis 2013. Meter-sized Moonlet Population in Saturn’s C Ring and Cassini Division. Astron J.145, 171, doi:10.1088/0004-6256/145/6/171.
Marouf, E. A., French, R. G., Rappaport, N. J., McGhee, C. A., Wong, K., Thomson, F. S., Anabtawi, A. 2006. Structure and properties of Saturn’s Ring B from Cassini radio occultations. Bull. Am. Astron. Soc. 38, 552.
How to cite: Colwell, J., Brooks, M., Jerousek, R., Coleman, C., Lina, K., Rothermich, A., and Esposito, L.: Phantoms in the Dark: Mesoscale Openings in the Core of Saturn’s B Ring, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-858, https://doi.org/10.5194/epsc2021-858, 2021.
Cassini’s Ultraviolet Imaging Spectrograph (UVIS) observed 276 stellar occultations of Saturn’s rings over the course of its mission. During these occultations, UVIS’ High-Speed Photometer (HSP) collected photon count measurements through the rings at a typical radial resolution of 10 meters from a wide range of viewing angles. Because photon counts are Poisson distributed, the variance of the starlight is approximately equal to its mean in the absence of occulting ring material. When the star passes behind the rings from the point-of view of the spacecraft, the finite sizes of the ring particles result in an excess variance above the mean caused by correlation in the blocking of photons. Showalter and Nicholson (1990, Icarus, 87, 285) and Colwell et al. (2018, Icarus, 300, 150) interpreted this excess variance in terms of an effective particle or clump size, RE, which depends on the length scale of shadows cast by particles and clumps. In the A ring however, where ring particles aggregate into trailing spiral structures called self-gravity wakes (Colwell et al., 2006, Colwell et al., 2007, Hedman et al., 2007, Nicholson and Hedman (2010), the assumptions of Showalter and Nicholson (1990) and Colwell et al. (2018) of uncorrelated spherical particles are invalid.
Here we expand their analyses to account for the presence of self-gravity wakes, ephemeral agglomerations of ring particles under the competing influence of their mutual self-gravity and Keplerian shear, by introducing free parameters S(wake separation), and W (wake width) into a direct calculation of higher order statistical moments of excess variance, skewness, and kurtosis from the expectation value of the random variate, ring transparency (T). We use the granola bar model of self-gravity wakes (Colwell et al. 2006) to calculate the autocovariance of the measured signal. In this work we compare the values of these higher order moments in the peaks and troughs of the Janus 2:1, Pandora 5:4, Janus 5:4, and Janus 6:5 density waves, which exist in regions in which self-gravity wakes are prominent. We compare the best-fit combinations of S and W to the excess variance for many combinations of S and W from different ring regions to reveal trends in the variation of wake properties by ring region. The sum S+W is constrained by the measured dispersion of the waves which gives the local surface mass density. We use this value to determine the Toomre most-unstable wavelength which we assume to be equal to the self-gravity wake wavelength (S+W) (Julian and Toomre, 1966).
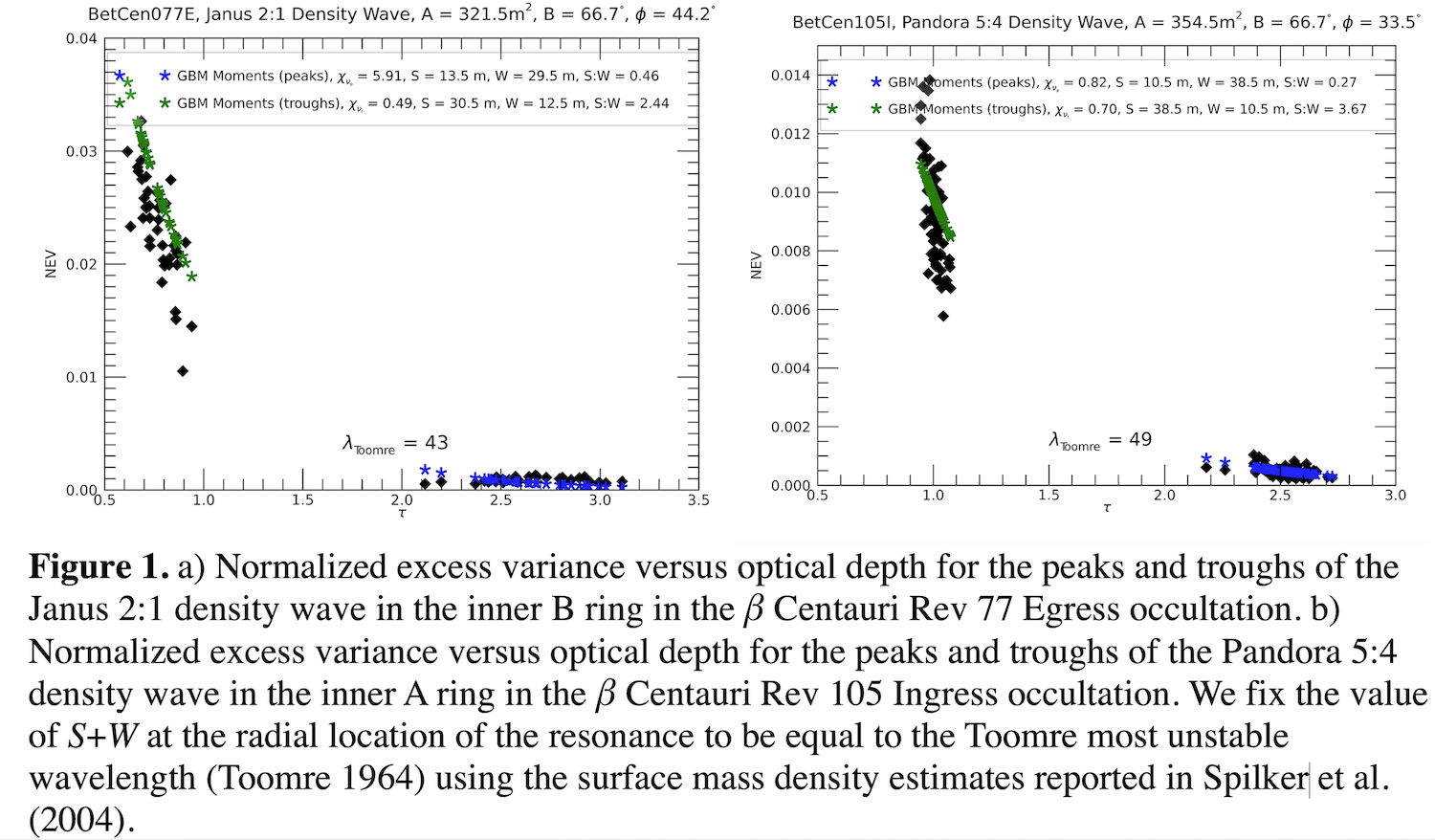
The second order moment, skewness (S), measures the asymmetry of the distribution and is indicative of either large clumps or small gaps in the rings nicknamed "ghosts" (Baillie et al., 2012). The presence of a few small gaps (high transparency outliers in the distribution) may lead to a positive skewness. The presence of too many gaps, however, increases the symmetry of the distribution as the gaps are no longer outliers. We take the ratio of S to τ to account for the correlation between the two variables (S is proportional to τ when τ ≳ 1). We occasionally observe that the ratio in the troughs differs by more than one standard deviation from the ratio in the peaks of the density waves. Our results indicate that either there are more gaps (positive outliers) present in the troughs than in the peaks or that there are so many gaps in the peaks that they no longer stand out as outliers of the distribution.
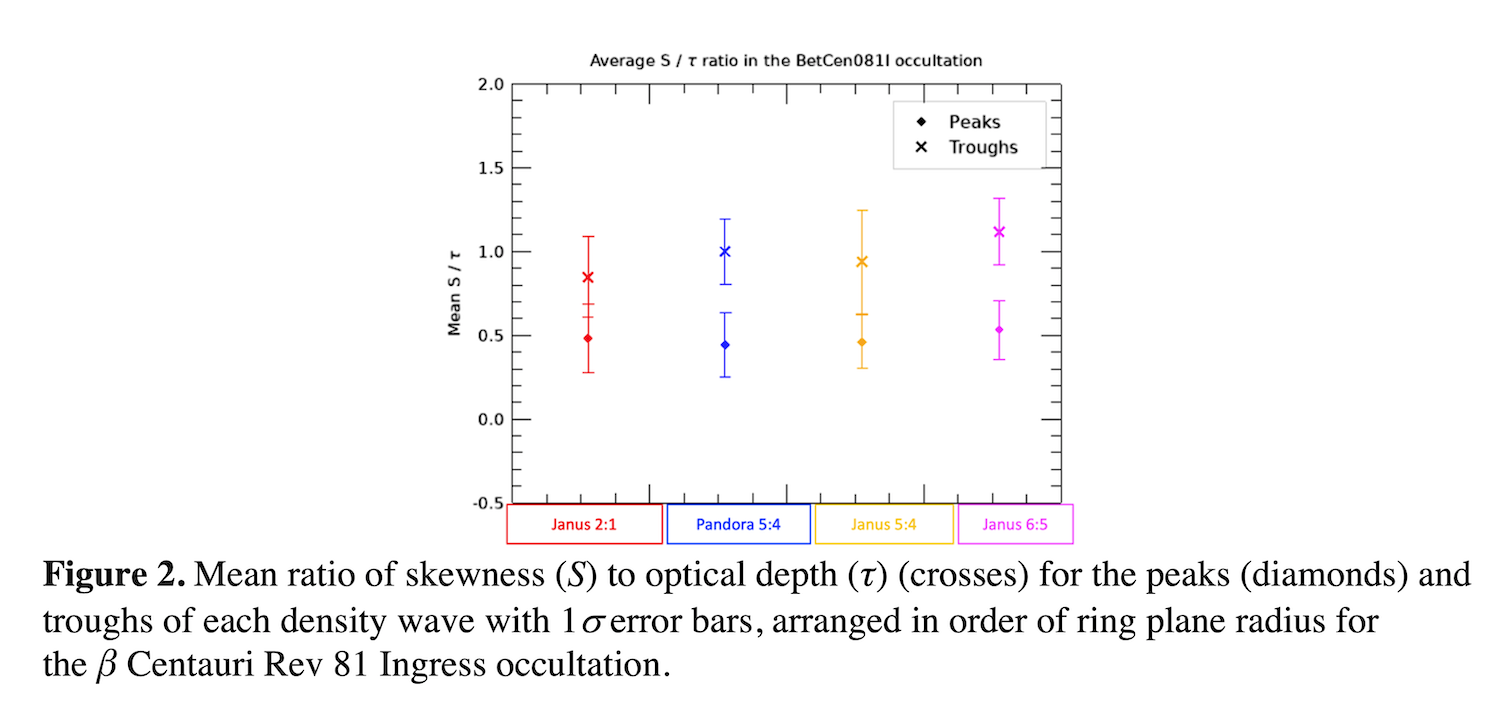
We apply this analysis technique to a multitude of occultations across a variety of ring elevation (B) and azimuthal (f) angles to survey wake parameter variation across these regions.
References
Baillié, K., Colwell, J.E., Lissauer, J.J., Esposito, L.W., Sremčević, M., 2011. Waves in Cassini UVIS stellar occultations 2: The C ring. Icarus 216, 292-308.
Colwell, J.E., et al., 2006. Gravitational wakes in Saturn’s A ring measured by stellar occultations from Cassini. Geophys. Res. Lett. 33.
Colwell, J.E., Esposito, L.W., Sremčević, M., Stewart, G.R., McClintock, W.E., 2007. Self-gravity wakes and radial structure of Saturn’s B ring. Icarus 190, 127-144.
Colwell, J. E., Esposito, L. W., Cooney, J. Particle sizes in Saturn’s rings from UVIS stellar occultations 1. Variations with ring region. Icarus 300, 150.
Hedman, M. M., et al., 2007. Self-gravity wake structures in Saturn’s A ring revealed by Cassini-VIMS. The Astronomical Journal 133(6), 2624-2629.
Jerousek, R. G., Colwell, J. E., Nicholson, P. D., Hedman, M. M., Esposito, L. W., 2016. Small Particles and Self-Gravity Wakes in Saturn’s Rings from UVIS and VIMS Stellar Occultations. Icarus 279, 36-50.
Julian, W.H. and Toomre, A. (1966). Non-axisymmetric responses of differentially rotating disks of stars. Astrophys. J., 146. 810-830.
Nicholson, P. D., and Hedman, M. M., 2010. Self-Gravity Wake Parameters in Saturn’s A and B Rings. Icarus 206, 410-423.
Showalter, M. R., and Nicholson, P. D., 1990. Saturn's rings through a microscope: Particle size constraints from the Voyager PPS scan. Icarus 87, 285-306.
Spilker, L. J., et al., 2004. Saturn A ring surface mass densities from spiral density wave dispersion behavior. Icarus 171, 372–390.
How to cite: Eckert, S., Colwell, J. E., Jerousek, R. G., Esposito, L. W., and Luthra, R.: Characterizing self-gravity wake morphology in Saturn’s rings from Cassini UVIS stellar occultation statistics, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-860, https://doi.org/10.5194/epsc2021-860, 2021.
The varying geometry of Cassini star occultations by Saturn’s rings constrains both the size and shape of structures that block starlight. Statistics of UVIS star occultations measure structures as small as meters, on times scales of minutes to decades. We calculate the excess variance, skewness and kurtosis including the effects of irregular particle shadows, along with a granola bar model of gaps, ghosts and clumps. The widths W and separation S of rectangular clumps play an analogous role to the relative size of the particle shadows, δ. In the first model considered, our calculations are based on the moments of the transparency T in that part of the ring Asampled by the occultation, thus extending the work of Showalter and Nicholson (1990) to larger τ and δ, and to higher central moments, without their simplifying assumptions. We also calculate these statistics using an approach based on the autocovariance, autocoskewness and autocokurtosis.
These new approaches compare well to the formula for excess variance from Showalter and Nicholson in the region where all are accurate, δτ≪1. Skewness for small τ has a different sign for transparent and opaque structures, distinguishing gaps from clumps. The higher order central moments are more sensitive to the extremes of the size distribution and opacity. We explain the upward curvature of the dependence of normalized excess variance for Saturn’s background C ring by the observation of Jerousek etal (2018) that the measured optical depth is correlated with particle size. For a linear dependence Reff = 12 * (τ – 0.08) + 1.8m from Jerousek’s results, we match the curvature of normalized excess variance, the skewness and the kurtosis in the region between 78,000 and 84,600 km from Saturn.
Statistics calculated from the granola bar model give different predictions from individual particles. The different τ dependence suggests that the wave crests compress the gaps more than the wakes, and produce more regularity among the clumps; and larger and more opaque self-gravity wakes in the wave crests, with transparent ghosts. The UVIS observations fall between the most regular and the most irregular granola bar models.
We compare selected occultations (Eckert etal 2020) at different values of the elevation B to estimate the flattening and axial ratio of ring particles and clumps. In Ring C, we find spheres: The statistical measures from multiple occultations follow the expected dependence on sin B, e.g. Showalter & Nicholson (1990). However, in the Janus 2:1 and Mimas 5:3 density waves, the excess variance for stars β Cen, λ Sco and σ Sgr shows no B dependence. This is exactly the expectation for completely flat (H/W =0) self-gravity wakes that we have derived from the autocovariance of the wake shadows. A closer analysis of this particular case gives H/W < 0.04, different from Colwell etal (2007), suggesting wakes are more like linguine than granola bars.
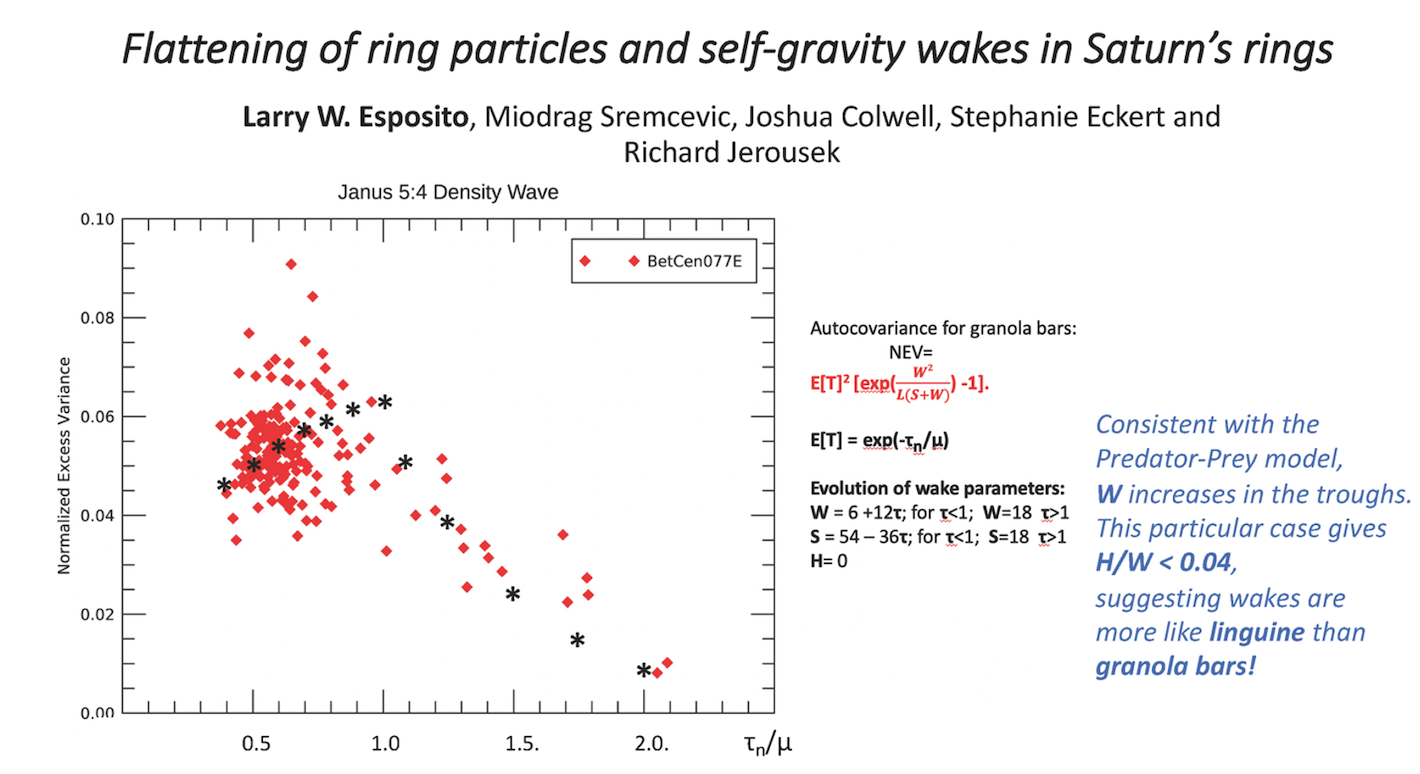
How to cite: Esposito, L. W., Sremcevic, M., Colwell, J., Eckert, S., and Jerousek, R.: Flattening of ring particles and self-gravity wakes in Saturn’s rings, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-854, https://doi.org/10.5194/epsc2021-854, 2021.
Binaries and multiple systems are common among young stars (Reipurth et al. 2014). These stars are often surrounded by discs of gas and dust, formed due to the conservation of angular momentum of the collapsing cloud, thought to be the site of planet formation.
In the case of binary systems, three discs can form: an outer disc surrounding all the stars (called circumbinary disc), and two inner discs around the stars. As circumbinary planets have recently been discovered by Kepler (see e.g., Martin 2018, Bonavita & Desidera 2020), it is crucial to understand the dynamics and evolution of circumbinary discs to better understand the initial conditions of planet formation in multiple systems.
The GG Tau A system is an example of a young multiple T Tauri star. The binary is surrounded by a bright disc, observed in the continuum emission at different wavelengths (see e.g., Guilloteau et al. 1999; Dutrey et al. 2014; Phuong et al. 2020b) and in scattered light (e.g., Duchene et al. 2014, Keppler et al. 2020). The disc extends in the dust from 180 to 280 au from the center of mass, and in the gas up to 850 au. The inner (<180 au) part is depleted in gas and dust. Scattered light images show a complex structure in the inner part of the disc, with arcs and filamentary structures connecting the outer ring with the arcs and three shadows.
Two different configurations are possible fitting the proper motion data for the system: a co-planar case with a low eccentricity binary with a semi-major axis of 34 au, explored by Cazzoletti et al. 2017 and Keppler et al. 2020, and a misaligned case (i=30) with an eccentric binary (e=0.45) and a wider semimajor axis of 60 au (Aly et al.2018). At the state of the art, all these analyses focused on the gas dynamics only.
We will show the results of new 3D SPH simulations of dust and gas performed with the code PHANTOM, devised to test the two possible scenarios. We will describe the dynamics of the system in the two cases, comparing our models with observational results in order to better constraint the orbital parameter of the GG Tau A system. Our predictions will guide future observing campaigns and shed light on the complex evolution of discs in triple stellar systems.
How to cite: Toci, C., Ceppi, S., Cuello, N., Lodato, G., Longarini, C., Ragusa, E., and Aly, H.: Exploring the dust ring in the circum-binary disc around GG Tau A, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-831, https://doi.org/10.5194/epsc2021-831, 2021.
Abstract
Large icy exomoons may represent a ubiquitous habitable environment yet remain on the fringes of detectability. Despite decades of progress in theoretical work, the nature and origin of the solids which form the building blocks of satellites remains a topic of debate. We utilize a radiation-thermochemical disk modeling code to study the time-dependent chemical evolution of volatiles prior to their incorporation into moons. We trace the evolving ice fraction and composition throughout an ensemble of disk models to match their evolving chemical state to solar system observables. We find that the expected evolutionary timescales of viscously evolving circumplanetary disks (103-105 yr) are not generally sufficient to allow chemical equilibrium to be reached, and that some degree of chemical inheritance from the circumstellar disk may be necessary in the form of meter-sized boulders which retain their volatiles during shock heating or even larger objects.
Introduction
Icy satellites and minor bodies are the most prevalent of the Solar System worlds known or suspected to host oceans of liquid water [1]. The bulk composition of the satellite ices may contain chemical impurities ranging from 0.1-15% by mass fraction [2]. The melting point of ice mixtures can be depressed by the presence of Ammonia, Methanol, or salts. Hence the composition of the volatile reservoir from which icy satellites form is of relevance to the presence of subsurface oceans, their geothermal and -physical evolution [3], the interpretation of in-situ measurements [4], and the eventual atmospheric composition [5].
The exact process by which moon formation occurs in circumplanetary disks (CPDs) is still a matter of debate. A general feature of regular satellite formation scenarios is that the CPD consists of circumstellar material accreted from within the vicinity of the planet [6]. Modeling of the outer solar circumstellar disk suggests a possible ammonia fraction relative to water NH3/H2O = 0.14, with as much as 80% of the nitrogen locked into NH3 [7].
Once a sufficiently massive planet has opened a gap in its circumstellar disk, accretion onto the CPD slows but does not stop as circumstellar material continues to flow into the vicinity of the planet [8]. Gas falling supersonically onto the CPD may pass through one or more accretion shocks and could be heated to >1000 K [9][10] destroying molecules in the accretion flow and potentially altering the eventual composition of satellites in a "reset" scenario.
The potentially short viscous timescale in which CPDs radially transport material suggests that they may be unable to reach chemical equilibrium before solid material is lost or incorporated into satellites. We must consider the time-dependant chemical evolution of the CPDs to determine whether inheritance may be necessary to reproduce the observed bulk composition of the icy satellites. If inheritance is necessary, CPDs may need to acquire their solids in larger (> 1 m) boulders able to retain their volatiles during gap crossing and shock heating.
Methodology
We aim to investigate the consequences of a chemical reset on the final composition of ices in chemically evolving circumplanetary disks by expanding the network of chemical reactions previously considered and taking into account the relatively short period in which chemical evolution can occur prior to moon formation. We will analyze the CPD time-dependant chemistry and determine the timescales for chemical equilibration relative to viscous diffusion, and extract bulk volatile satellite compositions given a variety of plausible disk properties. We will determine which scenarios are consistent with in-situ coeval formation of satellites and which suggest sequential formation and migration. Additionally We will determine whether limits on the CPD viscosity, accretion rate, and dust-to-gas ratio can be determined by the relevant timescales of chemical evolution versus radial transport. We use a radiation thermo-chemical disk model ProDiMo (PROtoplanetary DIsk MOdel) to explore the resulting abundance of various ices in a model grid of CPDs [11][12][13].
Figure 1: The radial ice-to-rock ratio in a Jovian circumplanetary disk model. The black dashed lined indicates the a steady-state chemical equilibrium , while the colored lines trace the evolving ice-to-rock ratio over 106 years. The black circles indicate the radial location and ice content of the Galilean satellites.
[1] Nimmo & Pappalardo 2016, Journal of Geophysical Research: Planets, 121, 8 [2] McKinnon et al. 2008, The Solar System Beyond Neptune [3] Hammond et al. 2018, Journal of Geophysical Research: Planets 123, 12 [4] Vance et al. 2018, Journal of Geophysical Research: Planets 123, 1 [5] Glein 2015, Icarus 250, 570-586 [6] Canup & Ward 2002, Astronomical Journal 124, p.3404-3423 [7] Dodson-Robinson et al. 2009, Icarus 200, 2 [8] Kley 1999, Monthly Notices of the Royal Astronomical Society 303, p.696-710 [9] Lubow et al. 1999, Astrophysical Journal 526, p.1001-1012 [10] Szulagyi & Mordasini 2017, Monthly Notices of the Royal Astronomical Society 465, 1 [11] Woitke et al. 2009, Astronomy and Astrophysics 501, p.383-406 [12] Kamp et al. 2010, Astronomy and Astrophysics 510, A18 [13] Thi et al. 2011, Monthly Notices of the Royal Astronomical Society 412, 2
How to cite: Oberg, N., Kamp, I., and Cazaux, S.: The Chemical Inheritance of Icy Moons, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-608, https://doi.org/10.5194/epsc2021-608, 2021.
1 – Introduction
The early dynamical evolution of the Solar System is nowadays clear to be likely occurred in an non isolated context, like many studies of Sun evolution inside an Open Cluster suggest (see Pfalzner, 2015 for istance). Such a framework indicates us that even protoplanetary matter around young stars may evolve in complex environments, which is further proved by some recent observations of protoplanetary disks around stars in Open Clusters (Mann et al., 2015).
An important role in the evolution of a disk in a non isolated system may be played by secular perturbations due to the far field stars, and, on the other hand, by the strong perturbations induced, on a shorter time-scale, by the close fly-bys. Occasional encounters with passing-by stars may considerably affect the dynamical evolution of the gas and change the balance of distribution of matter around each star.
We aim to investigate such a framework by means of 3D numerical hydrodynamical simulations, schematizing a solar-like star+disk system perturbed by close encountering stars.
By means of a Lagrangian Smoothed Particles Hydrodynamics (SPH) scheme, we calculate the evolution of the gas by including also the thermal effects induced by both the propagation of the radiation through the optically thick disk and the effects of the radiation coming from the stars. The temperature profile of a disk, which is substantially dependent on the thermal scheme assumed, may determine the turbulent viscous evolution of the disk itself and its susceptibility to the strong macroscopical perturbations induced by fly-by events.
2 – gas mixing and gas migration
It is worth to consider some recent formation models according which the time scale of giant planet formation inside the disks may be less than 105 yr (Magni & Coradini, 2004; Brennecka et al., 2020), far shorter than the previous classical results which amount of the order of 106 yr . Such a framework changes considerably the action of the cluster in altering the disk evolution. As a matter of fact, on one hand, the role of far field star becames less prominent in influencing the destiny of a gaseous disk since the secular perturbations has a small interval of time to act. On the other hand, the early stages of an Open Cluster are typically characterized by a chaotic non-relaxed state, in which the close interactions have a substantially high probability to occur. Thus, if the key processes inside the disk happen in a relatively short time, the disks itself have good chances to undergo strong perturbations by close approaching stars during its crucial evolutionary phases close to the planet formation stage.
We are interested to investigate two peculiar phenomena connected to the transport of matter induced by fly-by perturbation. One is represented by the macroscopical transport of matter from the inner to the outer layers of the disk, which may explain a still opened question about the Solar System consisting in unexpected observation of crystalline sylicates in comets (Brownlee et al. 2006). Despite sylicate compounds in comets are expected to be amorphous, they present a crystalline structure which need to be generated in the hot inner regions, hence incompatible with the current cometary distances from the sun.
On the other hand, we focus our attention to gas swapping among stars consisting in substantial capture and migration of matter towards another star during a close encounter. The simplest case that may happen is characterized by a star, previously lacking of any gas distribution around, that acquires a new disk. But a rather more complex situation occurs when gas migrates towards another disk during its phases of gaseous planet formation, altering the planetary cores feeding process.
The figure 1 shows an interesting example of gas migrated and captured by an approaching star, the sequence illustrates the main phases of truncation of a protoplanetary revolving around a single solar-like star, and further formation of a secondary tiny disk around the second star.

3 – Numerical method
We implemented an SPH based code to integrate the hydrodynamical evolution of disks, with a tree code based algorithm to account for their selfgravity. SPH algorithms represent a class of lagrangian schemes commonly employed to face a wide range of astronomical problems ( see for example Monaghan, 2005 or Price & Monaghan, 2007) involving self-grativating fluids. They employ a set of free moving particles which automatically mimic the gas density distribution into the 3D space without the need of any regular mesh-grid. This is an essential feature in problems where rather irregular distributions of gas are involved, like our investigation where the close interactions between 2 or more stars and a disk may substantially alter the original morphology of the disks and cause violent matter migration.
To perform the work, we developed an SPH algorithm (Pinto et al., 2019) to which we further added a radiative transfer scheme (according to the schematization of Viau et al., 2006) implemented with a careful study of the boundary conditions, due to the complex geometry and thermal exchange during a close encounter star–disk. This approach allows to describe a physically reasonable propagation of radiation through matter.
References:
- Brennecka et al. 2020, Science 370, 837–840
- Brownlee, D. et al. 2006, Science 314 , 1711 DOI: 10.1126/science.1135840
- Mann, R. K., Andrews, S. M., Eisner, J. A., et al. 2015, ApJ, 802, 77
- Magni, G. and Coradini, A. 2004, Planetary and Space Science 52, 343
- Monaghan, J. J. 2005, Reports on Progress in Physics, 68:1703–1759
- Pfalzner, S., Davies, M. B., Gounelle, M., et al. 2015, Physica Scripta, 90, 068001
- Price, D. J. and Monaghan, J. J. 2007, MNRAS, 374:1347–1358
- Pinto, L. D., Capuzzo-Dolcetta, R., and Magni, G. 2019, A&A 628, A82
- Viau, S. , Bastien, P. & Cha, S.H. 2006, ApJ, 639:559–570
How to cite: Pinto, L. D., Capaccioni, F., and Magni, G.: Protoplanetary disks and stars interaction in young open clusters: study of gas migration and chemical mixing with an SPH treatment., Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-720, https://doi.org/10.5194/epsc2021-720, 2021.
Please decide on your access
Please use the buttons below to download the presentation materials or to visit the external website where the presentation is linked. Regarding the external link, please note that Copernicus Meetings cannot accept any liability for the content and the website you will visit.
Forward to presentation link
You are going to open an external link to the presentation as indicated by the authors. Copernicus Meetings cannot accept any liability for the content and the website you will visit.
We are sorry, but presentations are only available for users who registered for the conference. Thank you.
Please decide on your access
Please use the buttons below to download the presentation materials or to visit the external website where the presentation is linked. Regarding the external link, please note that Copernicus Meetings cannot accept any liability for the content and the website you will visit.
Forward to session asset
You are going to open an external link to the asset as indicated by the session. Copernicus Meetings cannot accept any liability for the content and the website you will visit.
We are sorry, but presentations are only available for users who registered for the conference. Thank you.

