The evolution of the gravity signature of impact structures on the lunar farside

Introduction: The morphology of impact basins formed during the first 700 Ma after the Moon-forming event (e.g., [1-2]) is affected by the impactor's size and velocity, and the thermal state of the crust and upper mantle, which is related to the cooling history of the Moon (e.g., [3-5]). Due to alteration and erosion of structural surface features by subsequent impact flux, the size of given basins cannot be determined unequivocally. High resolution Bouguer gravity data from the Gravity Recovery and Interior Laboratory (GRAIL) mission [6-7] show a strong positive anomaly in the center, surrounded by a gravity low for impact basins located at the lunar farside. The relationship between the size of these gravity patterns and basin diameter may allow for estimating the impactor's size and thermal state of the Moon at the time of impact (e.g., [3, 5, 8]).

Previous studies (e.g., [7, 9]) showed that basin formation processes are followed by isostatic adjustment and cooling processes. As a result, basin structures undergo relaxation processes, coupled with modifications in gravity signature. Therefore, the direct comparison of GRAIL data with gravity data from numerical models of basin formation may be questionable.

We summarize results of our systematic numerical modeling study on the influence of the thermal state and impactor size on basin formation processes [5]. Using observed gravity data as constraints for our numerical basin formation models allows for estimating the thermal conditions and the size of the impactor at the time of impact for observable basin structures [5].

Based on this work we now aim at considering isostatic compensation processes and show preliminary results on how to investigate the problem.

Methods: In our previous work, we account for different impactor sizes, crustal thicknesses, and thermal states of the Moon. Different depth-temperature profiles represent the lunar thermal evolution at 4.5 Ga ("warm"), 4.1 Ga ("intermediate") and 3.8 Ga ("cold"), which correspond to approximate basin ages. We correlate modeled Bouguer gravity from our models of basin formation with observed gravity signatures of 16 lunar farside basins.

To evaluate the state of isostatic equilibrium in our best-fit models, we use as a first attempt the isostatic model assuming the Airy concept. Here, different topographic heights are accommodated by changes in crustal thickness. With this approach, we can estimate the location of the crust-mantle boundary for our best-fit models to evaluate the state of isostatic compensation. 

Results: Figure 1 shows the transient crater (D_t) , the diameter of the largest crustal thickness (DLCT), and the diameter of the Bouguer anomaly from basin formation models (D_BA-mod) as a function of impactor size (L_imp). Apparently, D_t, DLCT, D_BA-mod depend on the target's thermal state (indicated by the colors). For impactors larger than 40 km in diameter the thermal state affects the size of the Bouguer anomaly [5].

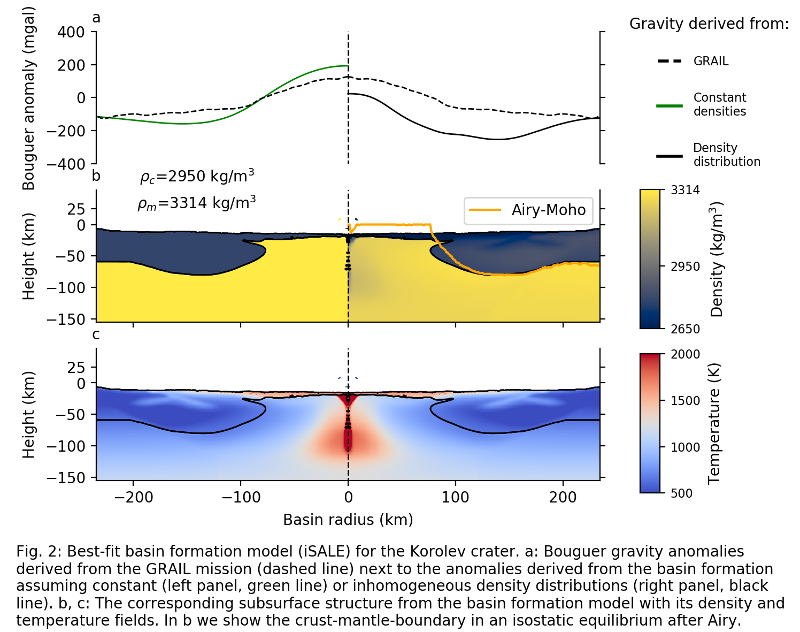
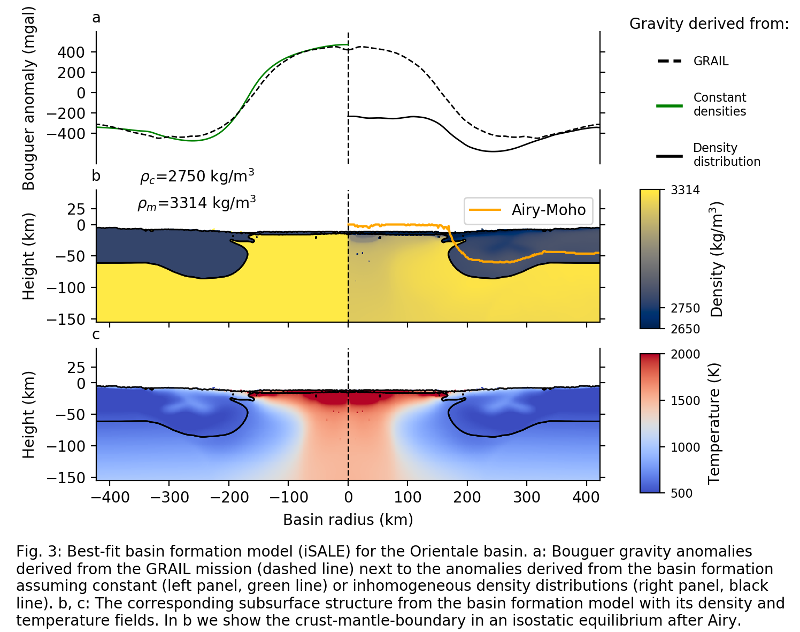
As examples, we discuss here the best-fit models for Korolev crater and Orientale basin: Figure 2 shows the model for the Korolev crater, assuming an impactor size of 50 km and a temperature profile at ca. 4.1 Ga. In Figure 3, the best-fit model for the Orientale basin formed by an impactor of 80 km in a cold lunar environment (3.8 Ga) is shown. The models are fitted to the observed gravity signal (Fig. 2a, 3a, dashed line). The green line (Fig. 2a, 3a) corresponds to the gravity anomaly derived from the basin formation model assuming constant densities in crust (ρ_c) and mantle (ρ_m) (Fig. 2b, 3b, left panel). The latter distinctly deviates from the density distribution in our basin formation models (Fig. 2b, 3b); however, we consider the usage of constant densities as a simple estimate of how Bouguer anomalies of our models may look like after cooling. The gravity signal (Fig. 2a, 3a; black line) based on the inhomogeneous density distribution due to the thermal expansion right after impact shows a much lower amplitude and a "plateau" in the basin center. A closer look to the temperature field (Fig. 2c, 3c) reveals that the "plateau" is directly related to the hot area of the temperature field. 

In order to assess the isostatic equilibrium of the basin formation models with the inhomogeneous density distribution, we determine the position of the crust-mantle-boundary according to the Airy concept (Fig. 2b, 3b, orange line). Our preliminary results show that the Korolev impact structure is almost in isostatic equilibrium, whereas large changes in the crust-mantle-boundary have to be assumed for the larger Orientale basin.

Conclusion: By assuming constant densities in the target, we are able to fit the observed and modeled gravity signatures. But this method of gravity fitting is questionable because the observed gravity data are based on the current subsurface density field, whereas the basin formation models show the density field directly after impact. We expect that cooling of impact structures between the last 4.4 Ga and 3.8 Ga directly affects the density distribution concomitant with isostatic compensation processes changing the position of the crust-mantle-boundary. Thus, the position of the gravity signal will also change.

Acknowledgements: We gratefully thank the developers of iSALE and the pySALEPlot tool. This work is funded by the Deutsche Forschungsgemeinschaft (Project-ID 263649064-TRR 170).

References: [1] Wilhelms, D.E. (1987) USGS Professional Paper 1348. [2] Morbidelli, A. et al. (2018) Icarus, 305, 262-276. [3] Miljkovic, K. et al. (2016) J. Geophys. Res. Planets, 121, 1695-1712. [4] Potter, R.W.K. et al. (2015) GSA Special Papers, 518, SPE518-506. [5] Lompa, T. et al. (2021) LPSC, Abstract #1254. [6] Zuber, M.T. et al. (2013) Science, 339, 668-671. [7] Melosh, H.J. et al., (2013) Science, 340, 1552-1555. [8] Neumann, G.A., et al. (2015) Sci. Adv., 1, e1500852. [9] Freed, A.M. et al. (2014) J. Geophys. Res. Planets, 119.