Modeling of a two-phase system with phase change, applications in planetology: Earth's inner core and Transneptunian objects

1. Introduction

We are interested in systems where two phases coexist: a solid phase with a high effective viscosity, and a low-viscosity liquid phase which fills the porosity of the solid phase. Two-phase systems, or "mush", are common in planetary sciences: magma extraction, Earth's inner core, icy moons... On terrestrial or icy bodies, such biphasic layers can compact under their own weight, which leads to the extraction of the liquid phase from the solid phase, and compaction of this solid phase. We present here a new model of two-phase flows with phase change (melting or freezing), and focus on 2 applications:

• Earth's inner core compaction: Whether the inner core crystallises dendritically or by sedimentation, it is likely that some liquid iron is trapped within the inner core, which may explain its low rigidity [1]. We extend here the studies of Sumita et al., 1996 [2] and Lasbleis et al., 2019 [3] by taking into account phase change within the inner core. 

• Transneptunian objects (TNOs): Ices may contain antifreezes like ammonia or methanol which could depress the melting point by up to 155 K [4]. Due to their presence, the melting temperature depends on their concentration. Then it is very likely that there would not be any clear border between solid and liquid if the melting point was reached, but rather a mushy layer. Several authors have studied the thermal evolution of TNOs without these considerations (for instance [5], [6], [7]).

 

2. Two-phase flow model

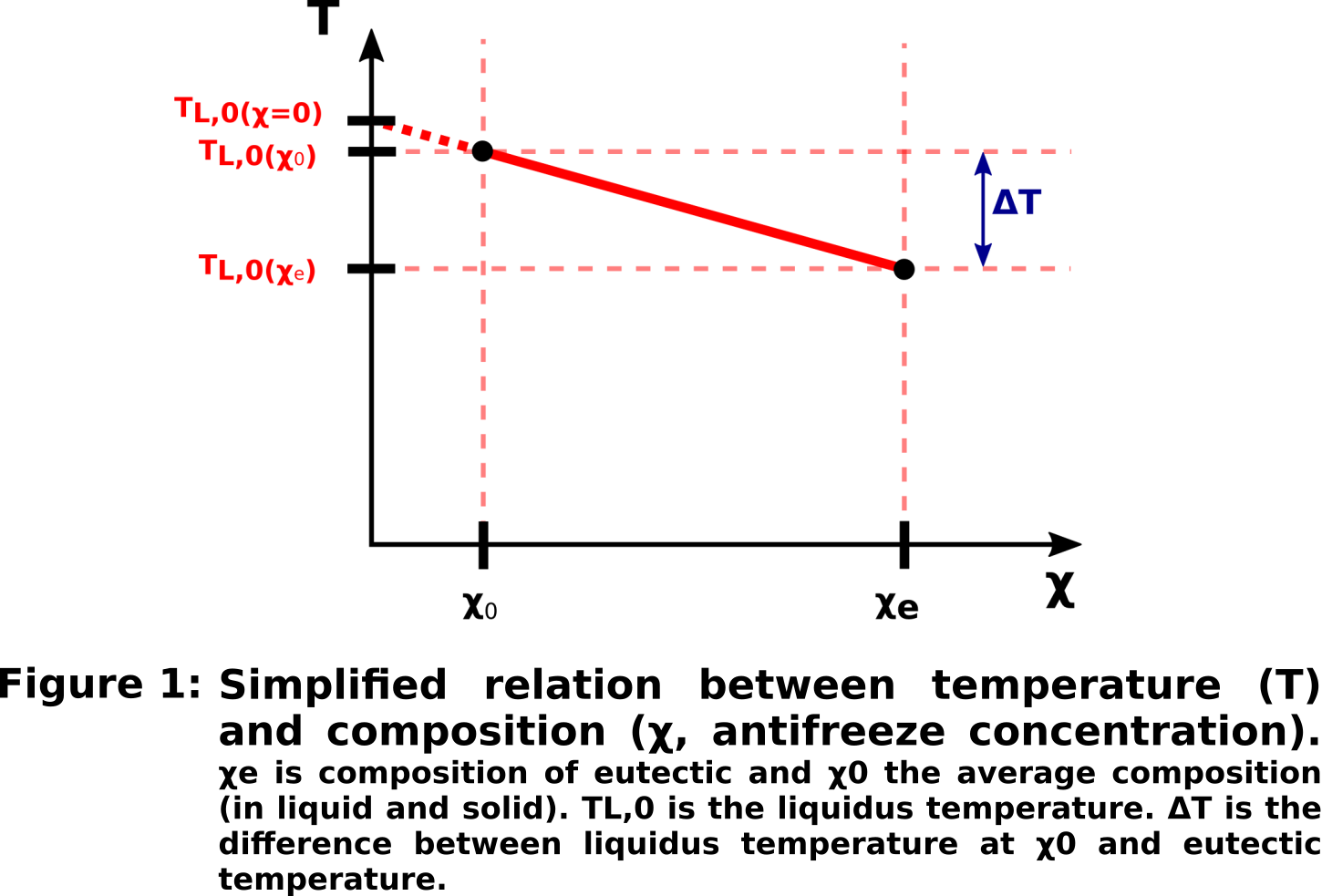
The model is based on the two-phase formalism developed by Bercovici et al., 2001 [8] for a non-reacting two-phase medium, which we generalise to allow for non-congruent phase change. This requires solving equations of conservation of mass and momentum for each phases, energy, and solute, with appropriate boundary conditions. In our model, the solid and liquid phases are assumed to be in thermodynamic equilibrium, which allows to link temperature and composition through the phase diagram. To simplify the problem, the liquidus temperature is taken to be linear (Fig. 1), which implies that the temperature in the two-phase region is a linear function of solute concentration. We further assume that the solute is considered to be totally contained in the melt (solid/liquid partition coefficient equal to 0). The set of equations is written in 1D spherical geometry. These assumptions allow us to reduce the system of equations to a system of only three equations (conservation of momentum, energy, and solute), which we solve to obtain the temperature (directly connected to composition), radial velocity of liquid (linked to velocity of solid) and porosity (the proportion of liquid).

The code solves equations in a 1D sphere, which size can evolve with time, either due to accretion (TNOs during their formation), or solidification (inner core). This is taken into account thanks to an adaptive grid. The code has been developed from the code written by Lasbleis et al., 2019 [3].

 

3. Preliminary results

Application to Earth's inner core

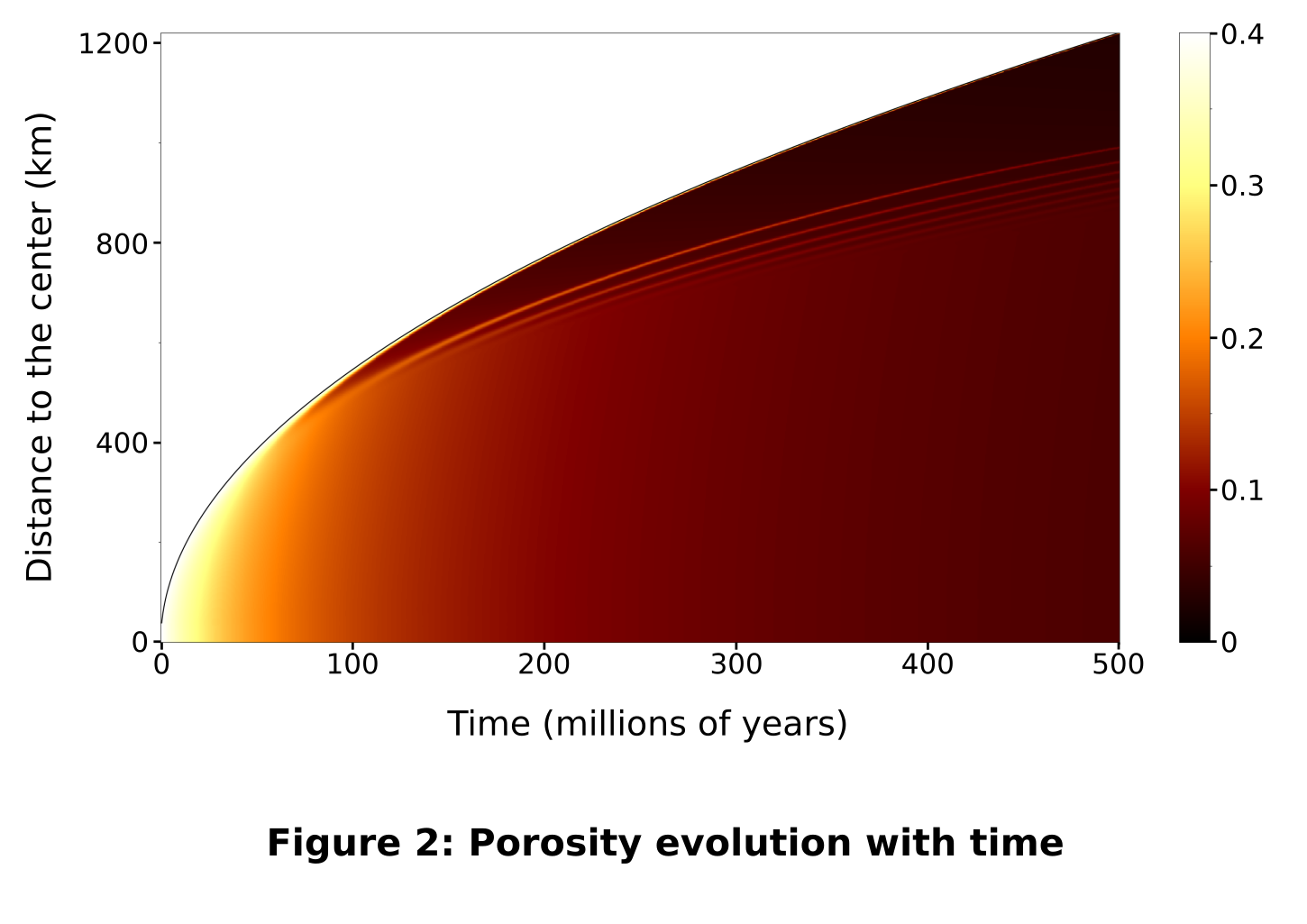
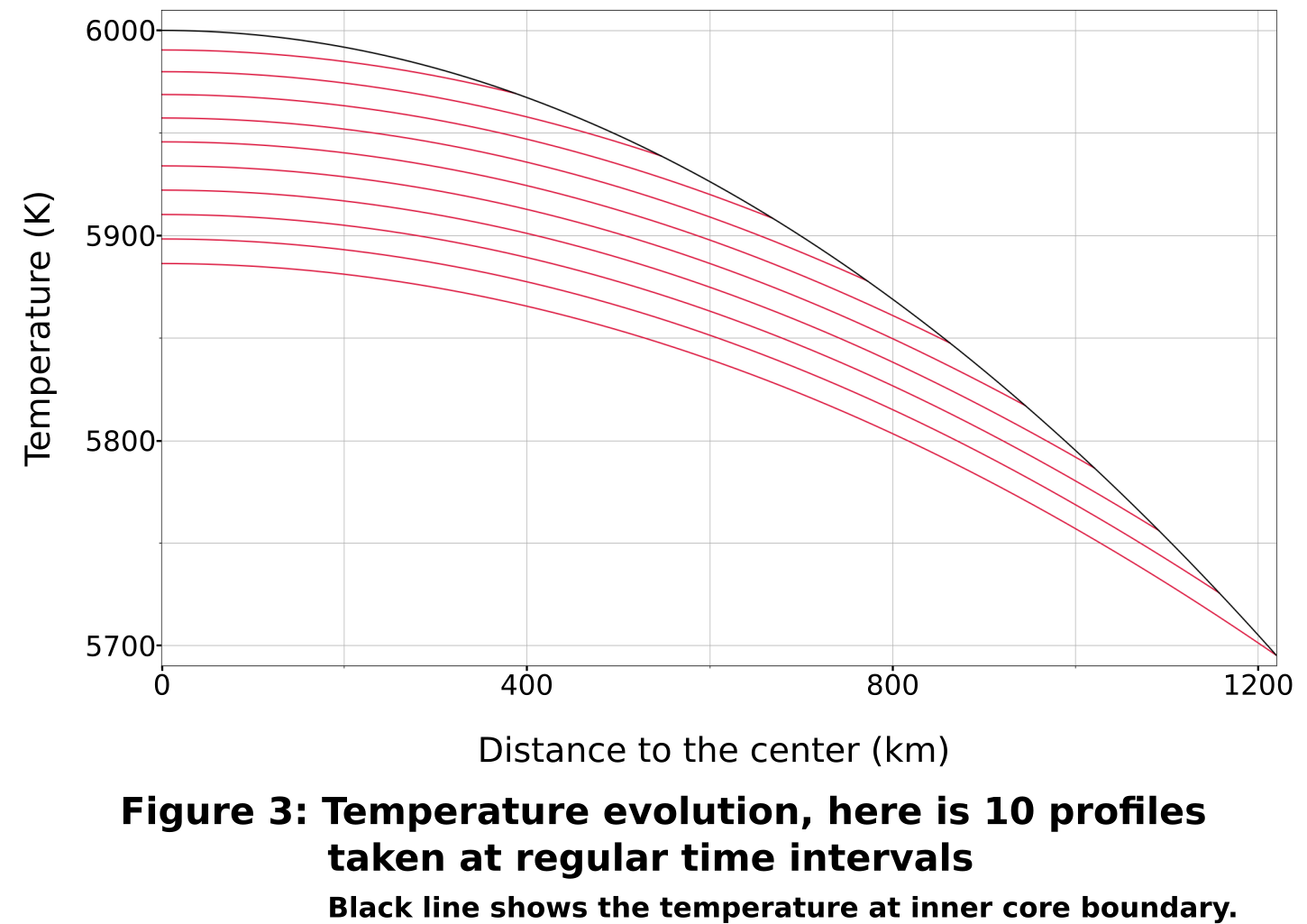
In the inner core, 'light elements', and in particular oxygen, act as antifreezes [9]. Within the inner core, the effect of pressure on the liquidus temperature cannot be neglected, and we thus take this factor into account in the model. The temperature-composition relation thus depends on pressure, or radius; the slope of the liquidus with respect to solute concentration is take to be constant but T_L decreases with decreasing pressure and increasing radius. At the inner core boundary, the temperature is set to T_L(χ₀, r). Fig. 2 and Fig. 3 show the evolution of porosity and temperature in the inner core as functions of time and radius.

 

Application to TNOs

When modeling the thermal evolution and differentiation of TNOs, our code has to be associated with an external icy diffusive spherical shell. If in addition we consider the formation of a rocky core, the mush (modeled by our code) is a spherical shell around a spherical rocky core. Our model takes into account the variations with temperature of ice thermal conductivity and heat capacity, which are far better known than for iron Earth's inner conditions [10] [11]. However, the pressure effect on T_L is negligible.

 

Acknowledgements

This project has received funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreements 802699 and 716429).

 

References

[1] Deguen, R. (2012). Earth and Planetary Science Letters, 333, 211-225.

[2] Sumita, I., Yoshida, S., Kumazawa, M., & Hamano, Y. (1996). Geophysical Journal International, 124(2), 502-524.

[3] Lasbleis, M., Kervazo, M., & Choblet, G. (2020). Geophysical Research Letters, 47(2), e2019GL085654.

[4] McKinnon, W. B., Prialnik, D., Stern, S. A., & Coradini, A. (2008). The solar system beyond Neptune, 1, 213-241.

[5] Bierson, C. J., Nimmo, F., & McKinnon, W. B. (2018). Icarus, 309, 207-219.

[6] Desch, S. J., & Neveu, M. (2017). Icarus, 287, 175-186.

[7] Malamud, U., & Prialnik, D. (2015). Icarus, 246, 21-36.

[8] Bercovici, D., Ricard, Y., & Schubert, G. (2001). Journal of Geophysical Research: Solid Earth, 106(B5), 8887-8906.

[9] Alfè, D., Gillan, M. J., & Price, G. D. (2002). Earth and Planetary Science Letters, 195(1-2), 91-98.

[10] Klinger, J. (1980). Science, 209(4453), 271-272.

[11] McCord, T. B., & Sotin, C. (2005). Journal of Geophysical Research: Planets, 110(E5).