Modelling of thermal stratification at the top of Mercury’s core

Introduction:

Thermal evolution studies of planet Mercury consistently predict that the heat flux at Mercury’s core-mantle boundary drops below the adiabatic heat flux early in Mercury’s evolution and thermally stratifies at least the outer part of Mercury’s core [1-3]. The deep dynamo explanation for Mercury’s broad-scale and low-intensity magnetic field suggests that a thick stratified liquid layer covers the convective dynamo region in Mercury’s core [4,5] and adds evidence that the top of Mercury’s core is stratified. In the simplest scenario that the liquid planetary core is well-mixed and that stratification of an upper liquid core layer is exclusively thermal in nature, the temperature profile satisfies the conduction equation in the stratified region of the core and it approaches the adiabat in the lower region of the core where heat fluxes are super-adiabatic.

Thermal evolution modelling of a core that is partly conductive and partly adiabatic involves a moving boundary problem in which the radius of the interface between the conductive region and the adiabatic region varies with time. One-dimensional thermal evolution models for the Earth have been performed that take thermal stratification into consideration by discretizing the core in many small spherically symmetric intervals [6]. For Mercury, Knibbe and van Westrenen (2018) have taken the development of a thermally stratified layer in consideration in a thermal evolution model [3]. They implemented a ‘steady-flux’ form of the temperature profile in the conductive region, by which we mean that they implemented the converged solution of the conduction problem where fluxes remain constant in time. This approach leads to a considerable numerical simplification, because discretizing the conductive part of the core is not needed. However, the approach is inconsistent with the time-variable fluxes that apply throughout Mercury’s evolution. We have recently improved the steady-flux approach of Knibbe and van Westrenen (2018) by the development of a numerical scheme that does not rely on the steady-flux assumption. Here, we present this method along with implications for Mercury’s thermal evolution.  

Method:

We developed a ‘piece-wise steady-flux’ (PWSF) numerical scheme, which solves one-dimensional thermal conduction problems up to arbitrary precision with increase of spatial resolution. This numerical scheme assumes a steady flux form of temperature in each of the intervals, which is continuous and differentiable in radial direction. These smoothness properties are convenient for implementing the numerical scheme in an energy-conserved thermal evolution approach for Mercury’s core, in which a conductive thermally stratified layer is considered that develops below the core-mantle boundary when the heat flux drops below the adiabatic heat flux. If a single interval is used by the numerical scheme, the method is equivalent to the steady-flux approach of Knibbe and van Westrenen (2018).

Results:

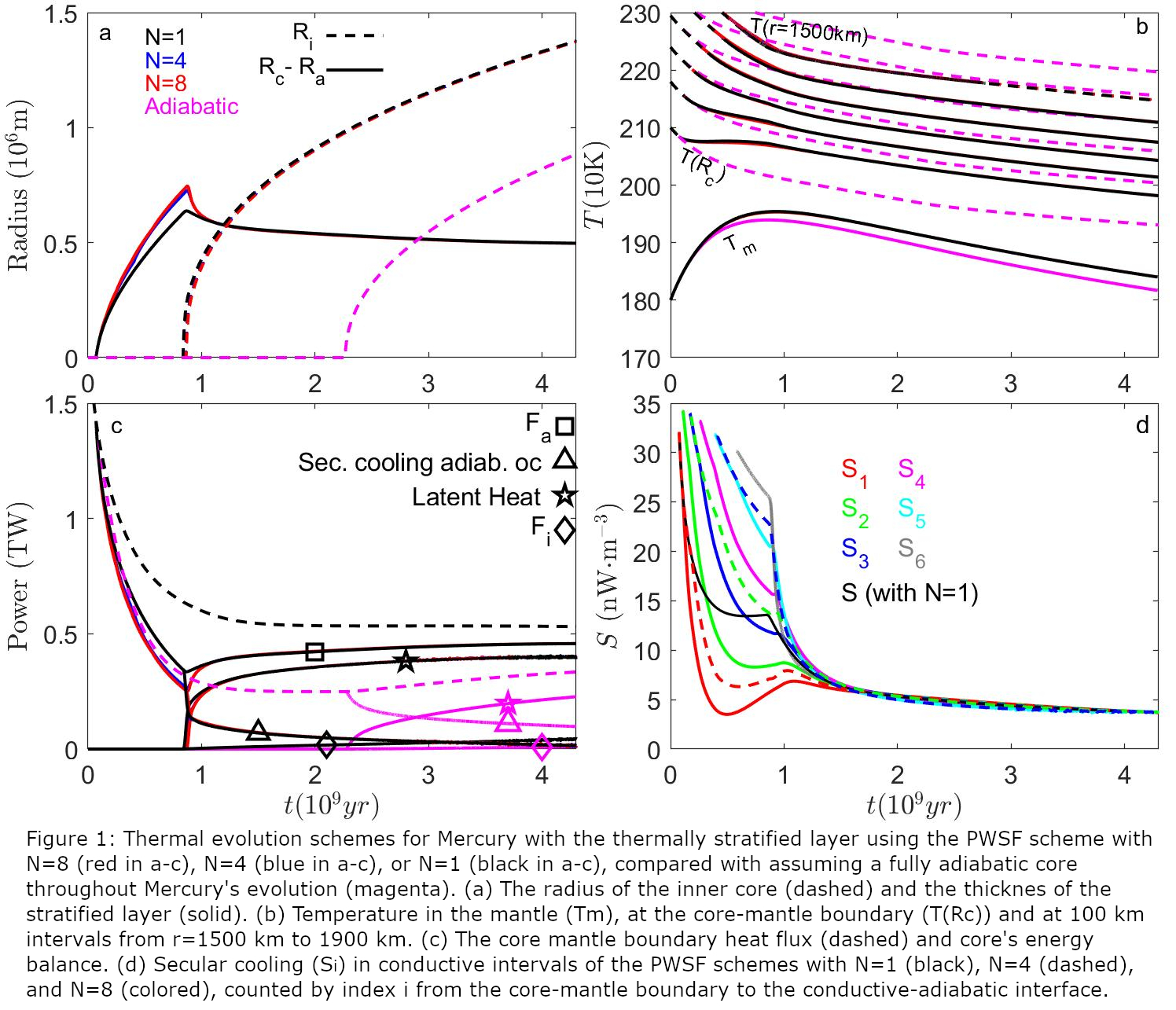
Figure 1 shows an example of a thermal evolution scheme for Mercury. The close similarity between the PWSF scheme with N=4 and that with N=8 (N being the number of adopted equal-volume intervals for the total core) indicates that N=4 is a sufficiently high resolution. For the PWSF scheme with N=1, the thermally stratified region of thickness R_c-R­_a grows at a slightly lower rate compared to the PWSF scheme with higher resolution, but for the rest the N=1 scheme shows a very similar thermal evolution as compared to those with higher resolution. After heat fluxes are stabilized (figure 1c), which is in this scenario at about 1 billion years where the inner core (R_i) starts to form (figure 1a), the PWSF scheme with N=1 becomes even more consistent with the PWSF schemes that use higher resolution. The reason is that the radial variation of average secular cooling within the stratified region becomes negligible (figure 1d). The similarity between the PWSF schemes with N=1 and with higher resolution suggests that the steady-flux approach of Knibbe and van Westrenen (2018) is appropriate for studying Mercury’s thermal evolution. 

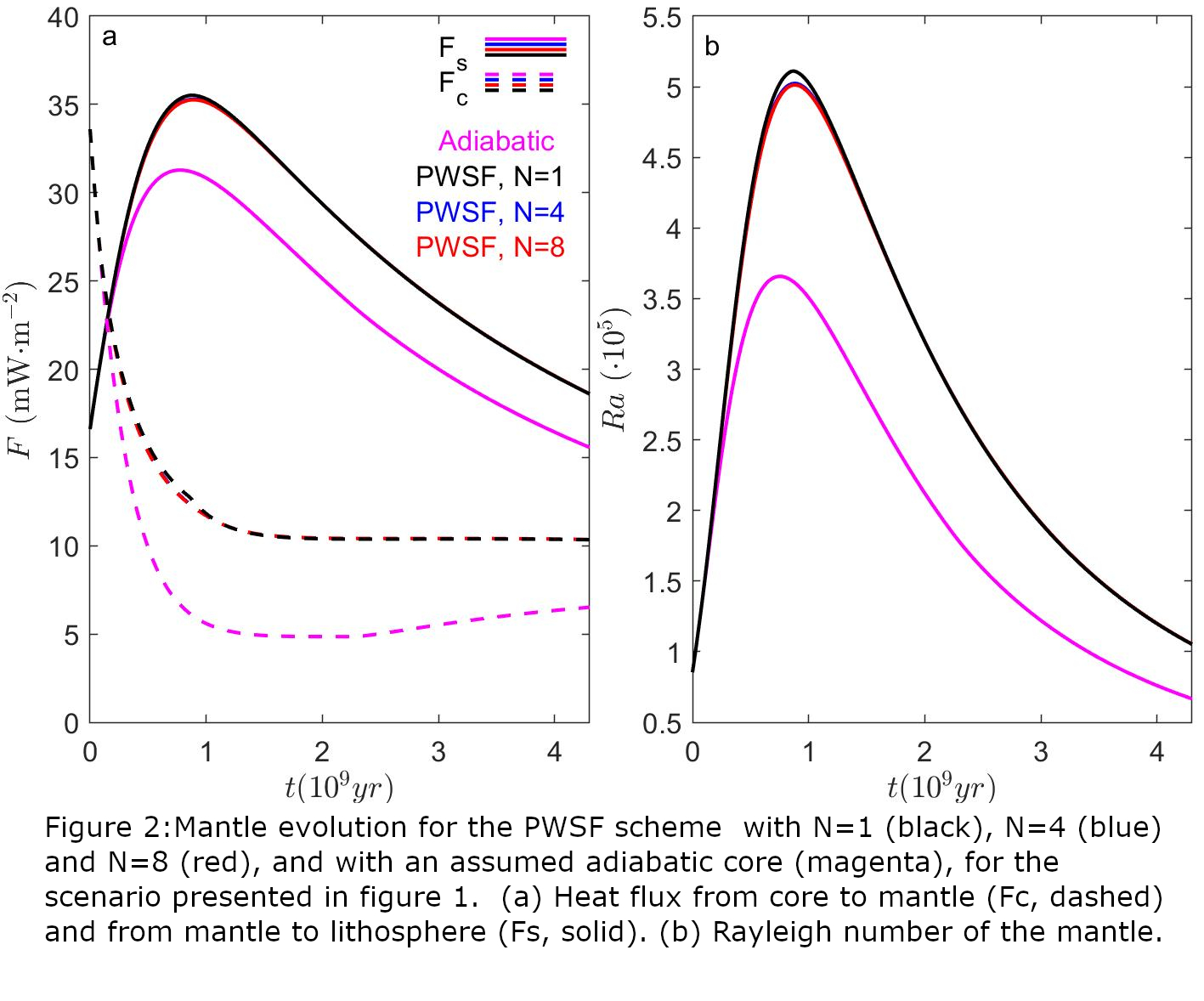
The implications of considering a thermally stratified layer in a thermal evolution model for Mercury are significant and cannot be neglected. By considering thermal stratification in a planetary core where the heat flux is lower than the adiabatic heat flux, radial variations in the cooling rate are accounted for whereas otherwise the distribution of energy in the core is fixed by the imposed adiabat. During the growth of the thermally stratified region to about 500 km in thickness (figure 1a), the deep part of the core cools more rapidly than the outer part of the core (figure 1b). Therefore, the inner core grows to a larger size (figure 1a) and the temperature and heat flux at the core-mantle boundary are higher and larger, respectively, if a thermally stratified region is considered (figure 1b and 1c). The higher heat flux into the mantle leads to a slightly higher mantle temperature (figure 1b) and higher heat flux through the silicate mantle. The latter is reflected by a larger heat flux into the lithosphere of Mercury (and larger heat flux out of the planet), and a higher Rayleigh number of the mantle (figure 2). These results indicate that the vigour and duration of mantle convection is underestimated if the evolution of a thermally stratified layer is not considered.

Details of the new thermal evolution model and of the consequences for Mercury’s thermal evolution will be presented in more detail at the conference.

[1] Stevenson D. J. et al. (1983) Icarus, 54(3), 466-489. [2] Tosi N. et al. (2013) JGR:Planets, 118(12), 2474-2487. [3] Knibbe J. S. and W. van Westrenen (2018), Earth Planet. Sci. Lett., 482, 147-159. [4] Christensen U. (2006), Nature, 444(7122), 1056-1058. [5] Takahashi et al. (2019) Nat. Comm., 10, 208. [6] Labrosse S. et al. (1997) Phys. Earth. Planet. Int., 99(1-2), 1-17.