Spectral unmixing with positivity, sparsity and group exclusivity constraints

Abstract

This work is related to the spectral unmixing problem, where the goal is to estimate the abundances corresponding to the decomposition of an observed spectrum into a linear mixture of "pure" spectra, called endmember. This problem is a classic problem of spectral analysis in planetary science, see for instance [1]. If the use of a dictionary including a large number of spectra allows to refine the model, it makes the estimation problem particularly difficult, these spectra being highly correlated between them. Using the tool developed in [2], we illustrate how additional constraints can improve the quality of the estimated mixtures. In particular group exclusivity (only one spectra per group of spectra), is promising to handle a complex spectral database. We discuss here how groups can be defined in a practical planetary science problem.

 

Method

We proposed to use a new approach for the linear unmixing problem, based on mixed integer programs (MIPs) [3], where a binary variable encodes the presence or absence of each dictionary element in the mixture. This formulation allows to model exactly a large variety of problems incorporating different types of constraints, among which :

- positivity/sum-to-one (POS): all abundances are positive and sum-to-one. Even though these constraints are becoming usual in spectral linear unmixing problems [1], we stress that MIP can easily encompass them.

- exact sparsity (SPA): A low number of non-zero abundances (called “active component”) is expected in the mixture [4]. Where classical sparsity methods are limited, the MIP reformulation allows to approach the problem in "l0 norm" in its exact form, i.e: a constraint on Kmax the maximum number of non-null elements.

- structuring the dictionary (Group Exclusivity GE):  We impose one active component among subgroups of spectra constituting the dictionary [5]. In the case of planetary surface, the definition of subgroups can be minerals, or family of minerals.

- minimum abundance (Significant Abundance SA): We constraint the abundances of the active components to be higher than a threshold. This constraint, relevant to model the search for significant components, is usually not addressed directly. Instead of a posteriori thresholding of abundances, MIP allows to directly include this constraint in the estimation of the abundances.

The resolution of optimization problems using MIP allows an exact resolution for problems of moderate size [2], which is often the case for the demixing problems. It has been shown that the solution can be reached in a reasonable time when the number of active components remains small (~10) for a spectral database composed of about 500 endmembers. 

We tested the results on the USGS spectral library [6], composed of 481 spectra, sampled in the 113 wavelength, based on the OMEGA hyperspectral imaging spectrometer [7]. To face any discrepancies between the spectral library and the real data, we also added synthetic slopes that mimic the effect of grain size and aerosols contribution [1].

Here we propose and discuss ways to design groups, meaningful for planetary science cases. In addition to the natural mineralogical groups (simply by names of mineral), we also designed groups of minerals, that we called “family”. In addition, we also add a special  family that contains the slopes, that are always active, in order to take into account the potential differences between spectral library and actual observation.

Results

Figure 1 shows a typical behavior in one synthetic example using different constraints. Figure 2 presents the same example as Figure 1, but with an alteration. The synthetic spectra is added by 0.1, in order to mimic a simple discrepancy between the spectral library and the actual data. In this case, one retrieved spectra is not exactly the same as the true one, but in the same family (both in the hematite group). Figure 3 presents the results of the proportion of the correct spectra/mineral/family that is retrieved as a function of SNR.

Discussion and conclusion

We proposed a way to group spectra into families and used this constraint to tackle the barrier of the limitation of the number of endmember in the spectral library. Group Exclusivity in addition to Significant Abundance or sparsity, seems a promising constraint to improve the spectral data analysis.

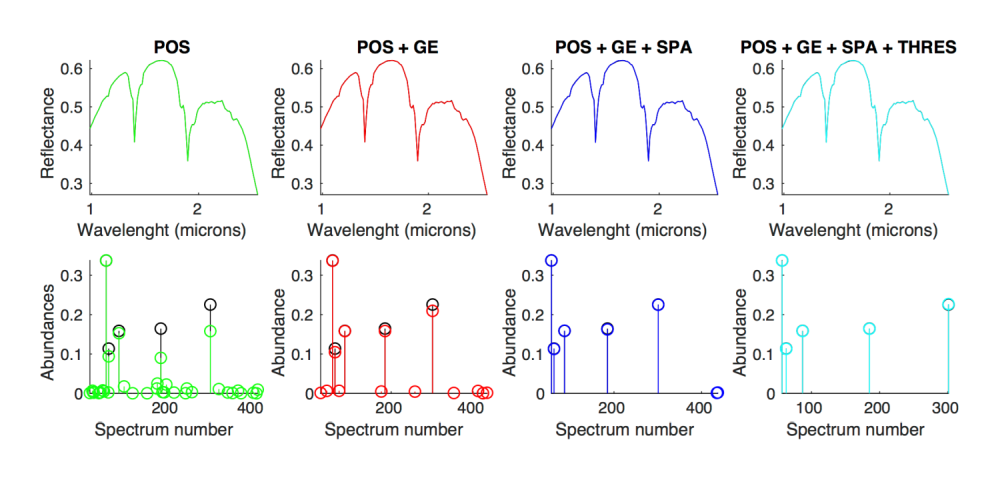
Figure 1 : Typical example of a mixture of Kmax=5 endmember out of 481 at noise level of 60 dB (very low noise level) black ground truth, color estimation. Using the POS constraints, the fit is acceptable, but the retrieved non null components are not corresponding to the actual active endmembers. By adding Group Exclusivity only (GE), all active components are detected. By adding sparsity (SPA) and significant abundance (SA), the results are drastically improved.

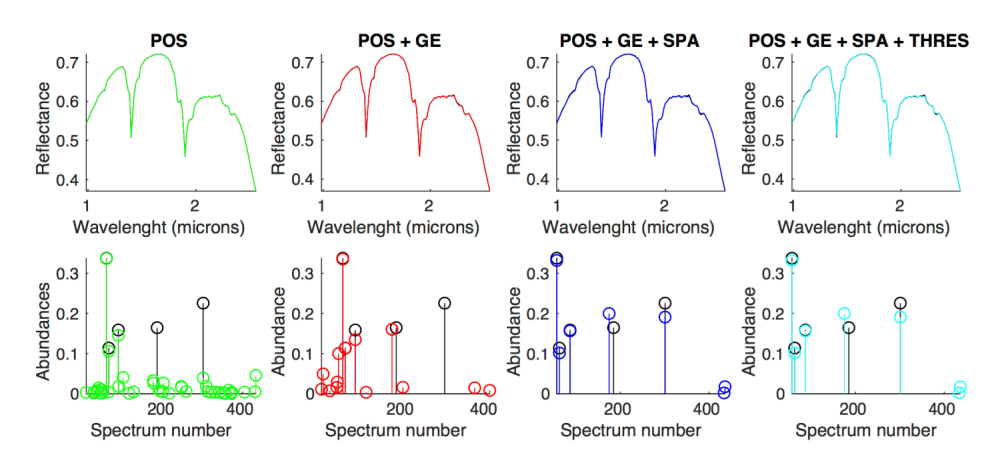
Figure 2: Same as Fig.1 but for a brighter synthetic spectra (synthetic spectra of Fig. 1 + 0.1). One detected spectra is not the same as the ground truth, but in the same family (hematite), leading to the same conclusion.

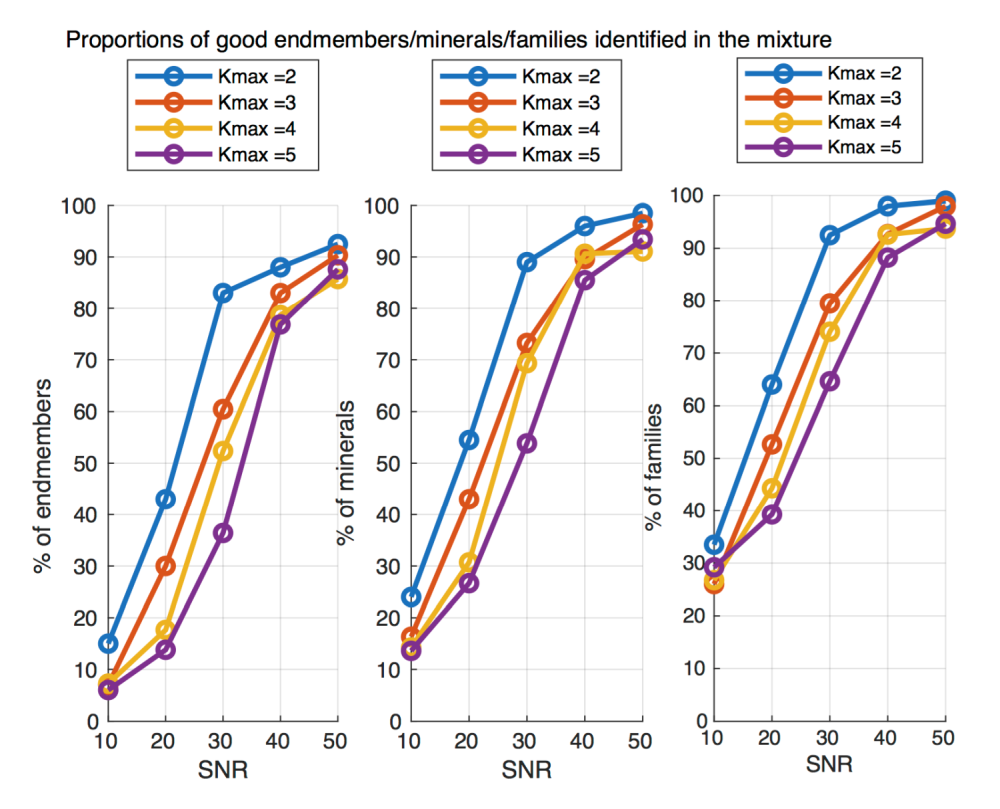
Figure 3: Average number of good endmember detection on 100 random examples, using POS + GE + SPA + THRES algorithm. At SNR 50, 90% of the endmembers are correctly detected, but 95% of the minerals (same mineral name), and 99% of the same family (same group of minerals).

   

Reference            

[1] F. Schmidt, M. Legendre, and S. Le Mouelic, “Minerals detection for hyperspectral images using adapted linear unmixing: LinMin,” Icarus, vol. 237, 2014.

[2] Ben Mhenni, R.; Bourguignon, S.; Ninin, J. & Schmidt, F. Spectral Unmixing with Sparsity and Structuring Constraints Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), 2018 9th Workshop, held 23-26 September 2018, Amsterdam, The Netherlands, 2018, 1-4,

[3] S. Bourguignon, J. Ninin, H. Carfantan, and M. Mongeau, “Exact sparse approximation problems via mixed-integer programming : Formulations and computational performance,” IEEE Trans. Signal Process., vol. 64, no. 6, Mars 2016.

[4] M.D. Iordache, J.M. Bioucas-Dias, and A Plaza, “Sparse unmixing of hyperspectral data,” IEEE Trans. Geosci. Remote Sens., vol. 49, no. 6, Juin 2011.

[5] L. Drumetz, T. R. Meyer, J. Chanussot, A. L. Bertozzi and C. Jutten, "Hyperspectral Image Unmixing With Endmember Bundles and Group Sparsity Inducing Mixed Norms," in IEEE Transactions on Image Processing, 2019.

[6] Clark, R. N.; Swayze, G. A.; Wise, R.; Livo, K. E.; Hoefen, T. M.; Kokaly, R. F. & Sutley, S. J. USGS Digital Spectral Library splib05a U.S. Geological Survey, U.S. Geological Survey, 2003 http://speclab.cr.usgs.gov/spectral-lib.html

[7] Bibring, J. P.;et al., OMEGA: Observatoire pour la Minéralogie, l'Eau, les Glaces et l'Activité Mars Express: the Scientific Payload, 2004, 1240, 37-49,