Estimation of the interior density of a small body given its gravity field

Abstract

We present here a method for the retrieval of the internal density distribution of a small body, via a least squares inversion of its gravity field and rotational state. Multiple solutions are averaged in order to limit the effect of the a priori density distribution. Simulations show successful density map estimations even with little to no initial information on the interior structure of the body.

 

1. Introduction

The gravity field of a body is a property among the most readily obtainable by a spacecraft mission. Be it by employing radio-tracking, optical, or gravimetric data, several missions have provided and will provide gravity expansions of degree 2 and higher for small bodies. In turn, the extended gravity field is an effect of the distribution of the mass inside the body. However, the inverse problem of estimating the density distribution from the gravity field is not a trivial one, and generally with non-unique solutions [1].

Here, we propose a method to obtain a unique solution for the internal mass distribution of a small body by restricting our estimation to zones of constant density, which are limited in number by the accuracy of the gravity model [2]. Where available, additional observables such as the libration amplitudes could help in the estimation of the interior structure. Averaging of the solutions obtained for different subdivisions of zones provides then the estimated density map [3].

 

2. Methods

The code builds from available software which allows to compute the gravity harmonics of a body approximated by a collection of cubes, each with a given density [4]. Here, the cubes are grouped in subregions of constant density, as many as there are measured coefficients. Each subregion is assigned an initial density, from which the software computes gravity coefficients matching in degree and order those observed. The difference between the coefficients thus computed and the observed ones is then minimized in a least-squares sense [5]. The solution of the regularized least-squares inversion is the density for each of the initial zones, along with its uncertainty. However, this solution is heavily dependent on the initial subdivision of the body into zones. Hence, a wide range of possible initial zones is explored, and the corresponding density solutions averaged together. 

From such an average solution, a new set of subregions is generated, with the help of a blob detection algorithm [6]. Finally, the gravity coefficients are inverted using this new zone subdivision. This step is necessary because, while providing a good distribution of the density zones, the density values of the averaged map are biased by solutions coming from inaccurate initial zones subdivisions. 

The data used in the inversion are the spherical harmonics coefficients of the gravity field expansion. The advantage of these observables is that they can be measured without the need for specific payload. Although the method can be easily adapted to process surface gravity measurements, the larger errors on the surface gravity coming from the cubes discretization make it less appealing for these type of data.

 

3. Discussion and outlook

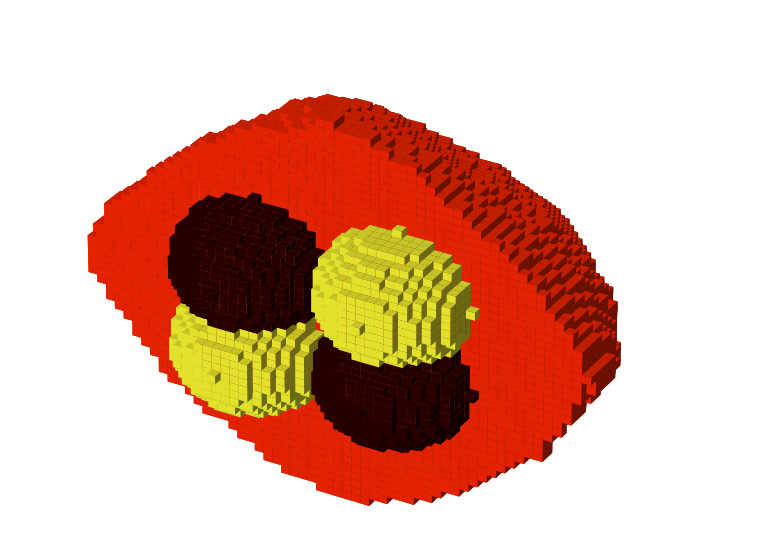
Figure 1 shows the results obtained when applying the method to a fictitious density distribution for asteroid Bennu. The nominal density distribution, shown in Figure 1a, was used to produce a synthetic gravity field expansion of degree 11. An optimistic noise profile was assumed for these simulated observables, with a 1% error on each gravity coefficient. The spherical harmonics coefficients were then inverted via the iterative process described in Section 2, resulting in the density distribution shown in Figure 1b. 

With a gravity field of this resolution, the inversion method is clearly able to distinguish the 4 density anomalies inside the body. Still, the comparison between the nominal and the estimated density models reveals the current limitations of the method in accurately reconstructing the size of the anomalies or their density — which is equivalent, given the constraint on the total mass. 

Once a better agreement between the retrieved and the nominal models will be achieved with the current (high) resolution of the gravity harmonics, the synthetic gravity fields will be truncated at lower degrees, making them more realistic as outputs of spacecraft missions to small bodies. Future simulation studies will also make use of more realistic noise profiles, with the errors on the observed coefficient increasing as a function of the degree.

(a)

(b)

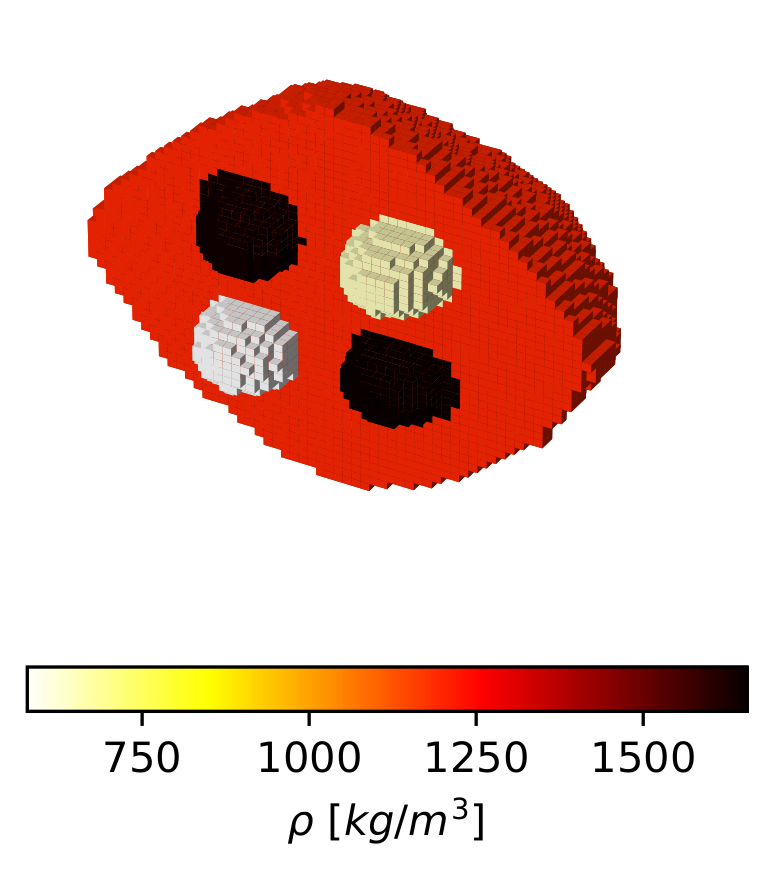
Figure 1: (a) density model used to simulate a degree-11 gravity field; (b) density distribution retrieved from said gravity field, without any initial assumptions about the true distribution

 

Acknowledgements

This work was financially supported by the French community of Belgium within the framework of a FRIA grant, and by the Belgian PRODEX program, managed by the European Space Agency in collaboration with the Belgian Federal Science Policy Office.

 

References

[1]  P. Tricarico. Global gravity inversion of bodies with arbitrary shape. Geophysical Journal International, 195(1):260–275, 2013.
[2]  Y. Takahashi and D. J. Scheeres. Morphology driven density distribution estimation for small bodies. Icarus, 233:179–193, 2014.
[3]  L.-I. Sorsa, M. Takala, P. Bambach, et al. Tomographic inversion of gravity gradient field for a synthetic Itokawa model. Icarus, 336:113425, 2020.
[4]  S. Le Maistre, A. Rivoldini, and P. Rosenblatt. Signature of Phobos’ interior structure in its gravity field and libration. Icarus, 321:272–290, 2019.
[5]  D. J. Scheeres, B. Khushalani, and R. A. Werner. Estimating asteroid density distributions from shape and gravity information. Planetary and Space Science, 48(10):965–971, 2000.
[6]  S. v. d. Walt, J. L. Schönberger, J. Nunez-Iglesias, et al. scikit-image: image processing in Python. PeerJ, 2:e453, 2014.