Rings around small bodies: the 1/3 resonance is key

Narrow and dense rings have been discovered around the small Centaur object Chariklo (Braga-Ribas et al 2014) and the dwarf planet Haumea (Ortiz et al. 2017). Both ring systems are observed close to the 1/3 resonance with the central body, meaning that the particles complete one revolution while the body completes three rotations.

The potential of small bodies can have large non-axisymmetric terms when compared to the giants planets. As a result, strong resonant couplings occur between the body and a surrounding collisional, dissipative disk (Sicardy et al. 2019). Those resonances are described by a critical angle φ= mλ' - (m-j)λ - jϖ, where j>0 is the resonant order (i.e. the order in eccentricity of the resonant term in the Hamiltonian), m (m<0 or m>0) is the azimuthal number, λ' (resp. λ) is the rotational angle of the body (resp. the particle), and ϖ is the longitude of periapse of the particle.

Among the j= 1 (Lindblad), 2, 3 and 4 resonances, only the cases j= 1 and 2 can have an unstable (more precisely non-elliptic) point at the origin of the phase portrait describing [X= e.cos(φ), Y= e.sin(φ)], where e is the eccentricity and φ is the critical angle previously defined. The 1/3 resonant in particular has m=-1  and j=2, and is thus of second order. For a narrow range of the Jacobi constant associated with that resonance [i.e. a - (3/2)a₀e², where a is the ring's semi-major axis and a₀ is the semi-major axis at exact resonance], the origin of the phase portrait is hyperbolic, hence unstable.

This instability triggers an eccentricity excitation of the ring near the 1/3 resonance, a source of torque on that ring. Such resonance can be created by a mass anomaly in the central body. We have tested this mechanism by simulating a ring with 30,000 particles undergoing inelastic collisions near the 1/3 resonance with Chariklo, in the presence of a large mass anomaly that represents 0.1 the mass of the body.

  

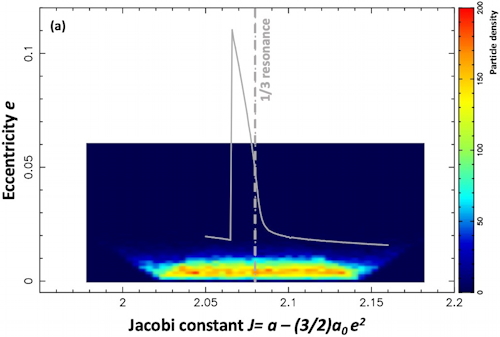
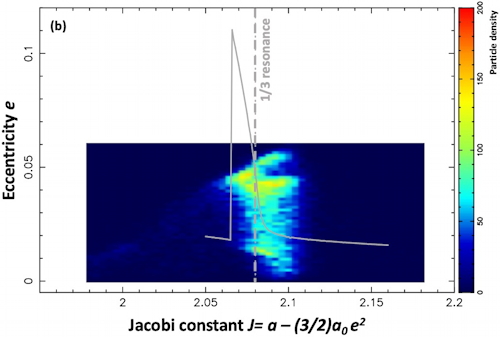
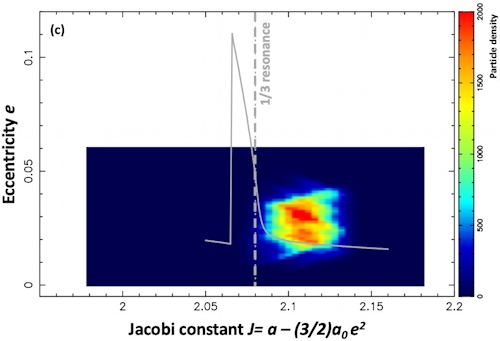
Preliminary results are shown in the figure above. The density of particles has been plotted in a (Jacobi constant-eccentricity) diagram, with the exact resonance location plotted as the vertical dash-dotted gray line. The solid gray line is the expected maximum eccentricity reached by particles for the corresponding Jacobi constant. Panel (a): initial conditions for the 30,000 ring particles; panel (b): the particles after 2,000 Chariklo rotations (about 1.6 years) during the excitation phase due to the 1/3 resonance; panel (c): the particles in the time interval 9,000-9,900 Chariklo rotations (~7-8 years). At that point, the ring has settled just outside the resonance location, reaching a balance between the eccentricity and semi-major dampings due to inelastic collisions, and the eccentricity excitation caused by the resonance.

More quantitative results will be presented, in particular the effect of smaller, more realistic, mass anomalies, and the assessment of a possible slow outward drift caused by a residual secular torque on the ring. Meanwhile, the observed behavior in those simulations appears as a promising mechanism to explain the proximity of both Chariklo's and Haumea's rings to the 1/3 resonance.

References
Braga-Ribas et al. 2014, Nature 508, 72
Ortiz et al. 2017, Nature 550, 219
Sicardy et al. 2019, Nature Astronomy 3, 146
Sicardy et al. 2020, in The Trans-Neptunian Solar System (Eds. D. Prialnik, M.A. Barucci and L. Young), Elsevier (Chapter 11)

Acknowledgements. The work leading to these results has received funding from the European Research Council under the European Community's H2020 2014-2021 ERC Grant Agreement n°669416 "Lucky Star".