TP15

EnVision is a proposed orbiter mission aiming at determining the nature and current state of Venus' geological evolution and its relationship with the atmosphere, to understand how and why Venus and Earth evolved so differently. It is is one of two M5 mission concepts in Phase A study with a final down-selection expected in June 2021. EnVision’s overall science goals are

- to characterise the sequence of events that generated the regional and global surface features of Venus, and characterize the geodynamics framework that controls the release of internal heat over Venus history; 

- to search for ongoing geological processes and determine whether the planet is active in the present era;

- to characterise regional and local geological units, to better assess whether Venus once had condensed liquid water on its surface and was thus perhaps hospitable for life in its early history.

EnVision will deliver new insights into geological history through complementary imagery, polarimetry, radiometry and spectroscopy of the surface coupled with subsurface sounding and gravity mapping; it will search for thermal, morphological, and gaseous signs of volcanic and other geological activity; and it will trace the fate of key volatile species from their sources and sinks at the surface through the clouds up to the mesosphere.

EnVision’s science payload consists of VenSAR, a dual polarization S-band radar also operating as microwave radiometer, three spectrometers VenSpec-M, VenSpec-U and VenSpec-H designed to observe the surface and atmosphere of Venus, and the Subsurface Radar Sounder (SRS), a High Frequency (HF) sounding radar to probe the subsurface. These are complemented by a radio science investigation which achieves gravity mapping and radio occultation of the atmosphere, for a comprehensive investigation of the Venusian surface, interior and atmosphere and their interactions.

How to cite: Widemann, T., Ghail, R., Wilson, C., and Titov, D.: EnVision: Understanding why Earth's closest neighbour is so different, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-414, https://doi.org/10.5194/epsc2021-414, 2021.

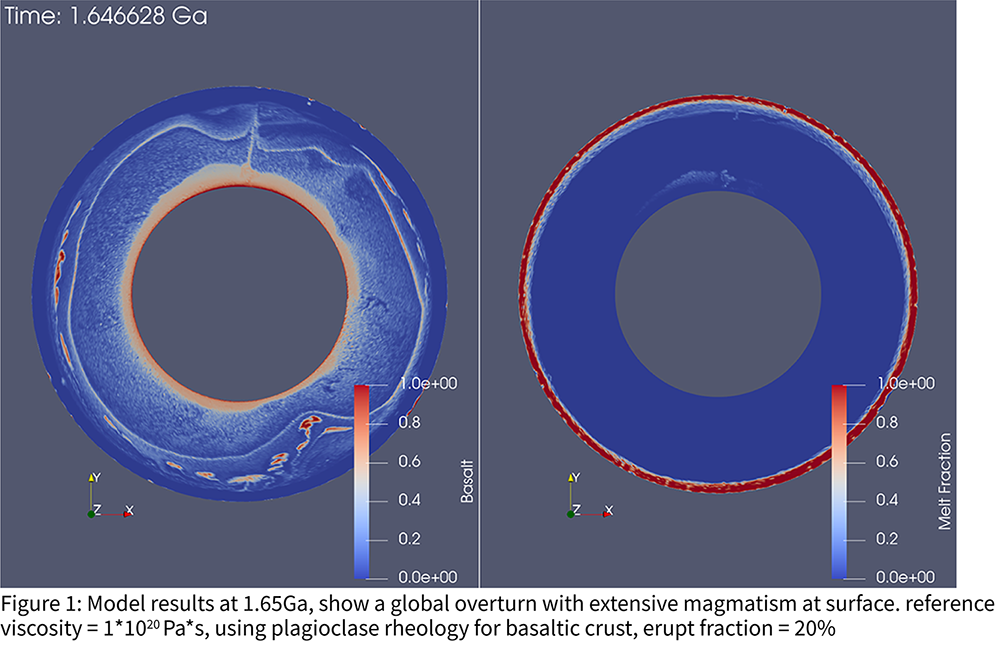
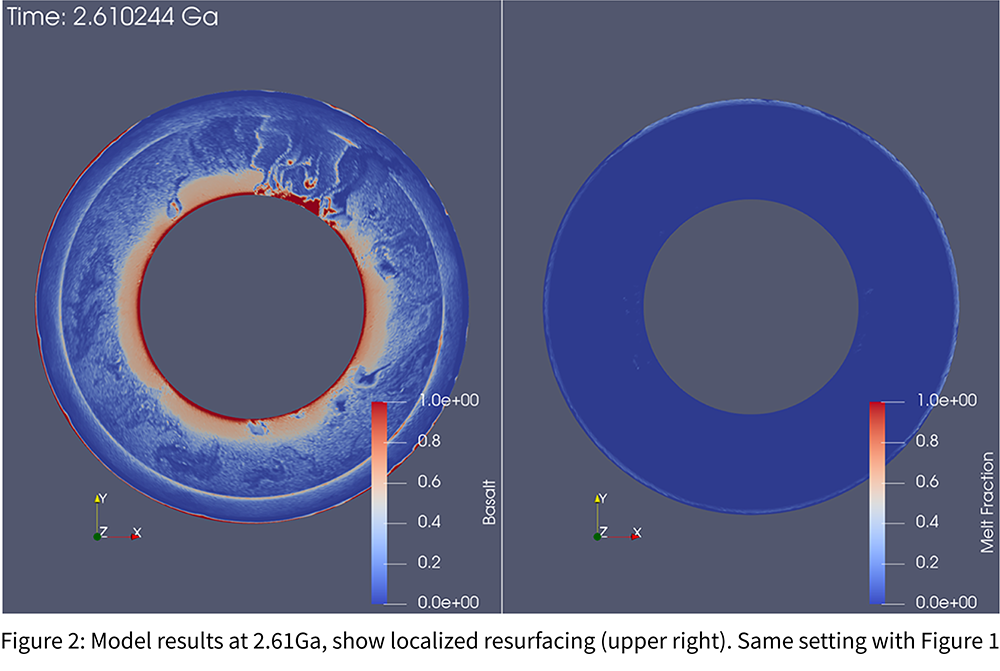
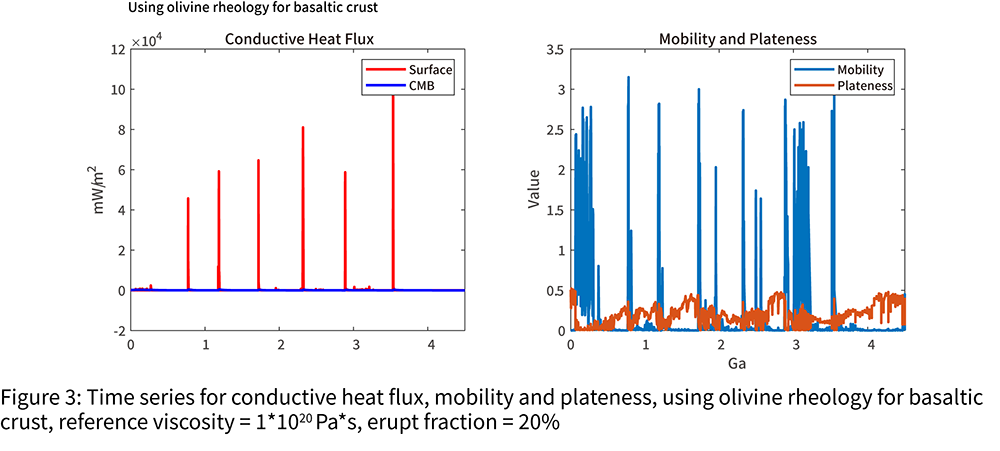
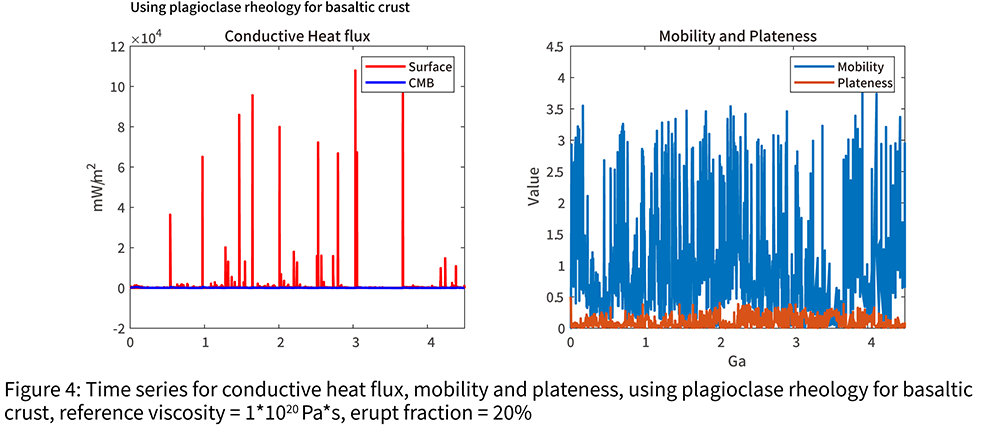
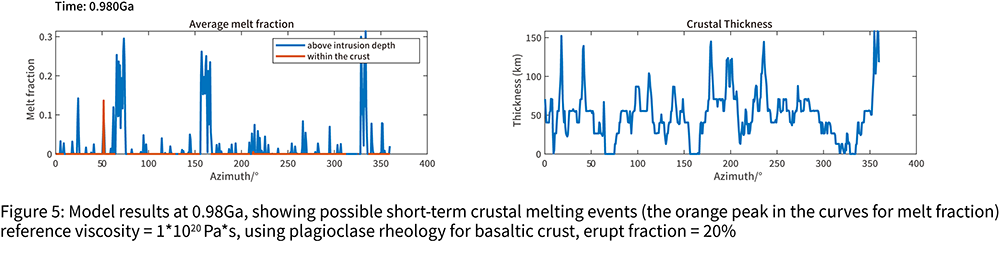
Introduction

An invaluable source of information about the present interior structure of Venus is the measurement of surface deflections and disturbances to the planet's gravity field caused by tidal deformation. The planet is mainly loaded by the semidiurnal solar tide that probes the interior at the angular frequency ω ≈ 1.25×10^-6 rad s^-1 [e.g., 1]. The tidal response is then determined by the rheological properties of the body.

In this work, we combine interior structure and tidal modeling of Venus to compute and compare measurable quantities, namely the tidal Love numbers k₂, the moment of inertia factor MoIF, and the tidal quality factor Q. Our predictions can be tested with future measurements, should current Venus mission proposals (e.g., Veritas and EnVision) be selected.

Interior structure and thermal state models

In order to calculate the tidal parameters (k₂ and Q), we first generate 1-D interior structure models of Venus. Our method is similar to that of [2] in which the interior is subdivided into chemically separated layers: an iron core, a rocky mantle, and a basaltic crust.

In addition, steady-state temperature profiles are calculated by applying a mixing-length approach [3], and we vary poorly constrained parameters (crustal density and thickness, iron content in the mantle, reference viscosity of mantle and core, surface and core-mantle heat fluxes).

Tidal deformation models

Tidal deformation modeling is based on the normal mode theory for a radially-stratified nonrotating incompressible viscoelastic sphere [e.g., 4]. In this approach, the deformations, tractions, and additional potential in the planet are expanded into spherical harmonics and the governing equations for the viscoelastic continuum are solved analytically. The resulting deformation state is then described by parametric functions, the parameters of which can be obtained from the boundary conditions.

We compute the potential Love numbers by using two different techniques. In the first approach, the radial profiles of the deformations, tractions, and additional potential are computed by using a matrix propagation method [e.g., 5, 6]. In the second approach, we seek directly the parameters of the aforementioned parametric functions [7].

We use the well-known Maxwell model for the core and adopt an Andrade model to compute the response of the Venusian mantle and crust [8, 9]. In contrast to the Maxwell model, the Andrade rheology accounts not only for the instantaneous elastic deformation and the viscous (steady-state) creep but also for the transient effects governed by the Andrade hereditary terms.

Results

(a) Comparison of Love numbers

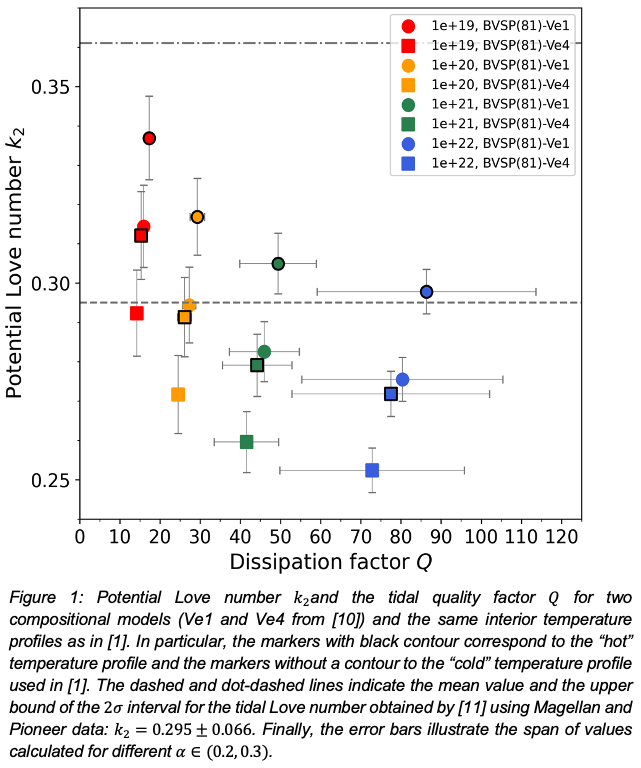
We select representative interior structure models and compute the tidal parameters according to the two methods described above. Both methods provide the same results for various sets of input parameters. Furthermore, we compare our results with published data from [1]. To this end, we used the same interior temperature profiles, core size, and viscosity as in [1], and employed two end-member compositions (i.e., BVSP(81)-Ve1 with a low and BVSP(81)-Ve4 with a high iron content in the Venusian mantle) similar to their models V1 and V4. Our results in Fig. 1, calculated with the tidal model of [7], are in close agreement with the data presented in Fig. 4 of  [1].

(b) Effect of mantle composition

We observe two distinct ranges of MoIF according to the bulk composition used in our interior structure models (Fig. 2). All models corresponding to the mantle mineralogy with a negligible low iron content [BVSP(81)-Ve1] are found at significantly lower MoIF than their iron-rich [BVSP(81)-Ve4] counterparts. Furthermore, it can be seen that an iron-rich mantle leads to smaller core sizes when comparing the two compositional models.

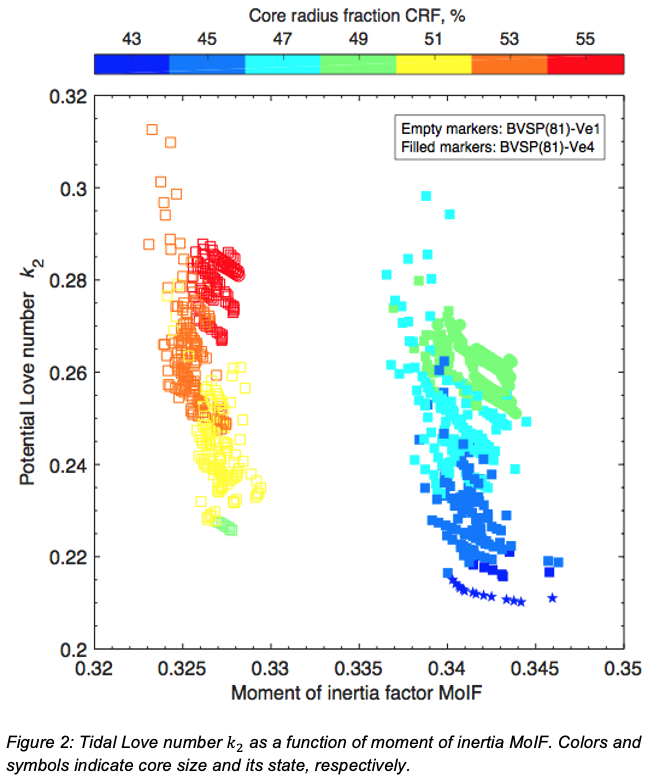
Combining the MoIF and the potential Love number k₂ delivers additional information about the state and size of the core. In Figure 2, the models with a completely solid core (stars) have the smallest core size and thus the lowest k₂, whereas the models with a completely liquid core (circles) have in general large core sizes and thus high k₂. In between these two end-members, we find the models with solid inner and liquid outer cores (squares). These models usually have medium-sized cores and intermediate potential Love numbers k₂. However, the highest k₂ value is obtained for models with partially liquid iron cores. Their much hotter counterparts with completely liquid cores, which would lead to even higher k₂, contain a fully molten mantle layer, and have been excluded here. Thus, the determination of the state and size of the core could be challenging for high potential Love numbers k₂ due to a model degeneracy from input parameters.

Conclusions

In this study, we have presented a comparison between two tidal deformation models [6,7] to compute Venusian tides. The results show a close agreement between the two tidal deformation models and the study of [1].

We have applied our interior models to investigate the effects of composition on the tidal parameters and moment of inertia factor. The results indicate two families of models with distinct MoIF that could be constrained by future measurements.

In the next step, we plan to combine the tidal deformation model with thermal evolution calculations to study the secular tidal evolution. To this end, we will couple the tidal model to 1-D parametrized [e.g., 12] and 2-D geodynamical [e.g., 13] models that treat the cooling history and melt production in the interior of Venus. Furthermore, our coupled tidal-thermal evolution model can be applied to study the interior of Venus-like extrasolar planets.

References

[1] Dumoulin, C. et al. (2017): JGR:Planets, 122.

[2] Sohl, F. & Spohn, T. (1997): JGR:Planets, 102(E1).

[3] Wagner, F. W. et al. (2019): GJI, 217(1).

[4] Sabadini, R. & Vermeersen, B. (2004): Springer.

[5] Segatz, M. et al. (1988): ICARUS, 75(2).

[6] Steinbrügge, G. et al. (2018): JGR:Planets, 123(10).

[7] Walterová, M. & Běhounková, M. (2020): ApJ, 900(1).

[8] Jackson, I. & Faul, U. H. (2010): PEPI, 183.

[9] Castillo‐Rogez, J. C. et al. (2011): JGR:Planets, 116(E9).

[10] Basaltic Volcanism Study Project (1981): Pergamon Press.

[11] Konopliv, A. S. & Yoder, C. F. (1996): GJI, 23(14).

[12] Tosi, N. et al. (2017): A&A, 605.

[13] Plesa, A.-C. & Breuer, D. (2021): LPSC, No. 2548.

How to cite: Walterova, M., Wagner, F. W., Plesa, A.-C., and Breuer, D.: Interior structure and tidal response of Venus: Implications for future missions, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-542, https://doi.org/10.5194/epsc2021-542, 2021.

Tidal forces acting on a planet cause a deformation and mass redistribution in its interior, involving surface motions and variation in the gravity field, which may be observed in geodetic experiments. The change in the gravitational field of the planet, due to the influence of an external gravity field, described primarily by its tidal Love number k of degree 2 (denoted by k₂) can be observed from analysis of a spacecraft radio tracking. The planet’s deformation is linked to its internal structure, most effectively to its density and rigidity. Hence the tidal Love number k₂ can be theoretically approximated for different planetary models, which means comparing the observed and theoretical calculation of k₂ of a planet is a window to its internal structure.

The terrestrial planet Venus is reminiscent of the Earth twin planet in size and density, which leads to the assumption that the Earth and Venus have similar internal structures. In this work, with a Venus we investigate the structure and elastic parameters of the planet’s major layers to calculate its frequency dependent tidal Love number k₂. The calculation of k₂ is done with ALMA, a Fortran 90 program by Spada [2008] for computing the tidal and load Love numbers using the Post-Widder Laplace inversion formula. We test the effect of different parameters in the Venus model (as a layer’s density, rigidity, viscosity and thickness) on the tidal Love numbers k₂ and different linear and non-linear combinations of k₂ andh₂ (as the tidal Love number h₂ describes the radial displacement due to tidal effects).

How to cite: Saliby, C., Fienga, A., Spada, G., Melini, D., and Memin, A.: Venus internal structure and global deformation, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-65, https://doi.org/10.5194/epsc2021-65, 2021.

Venus is commonly described as Earth’s slightly smaller twin planet. However, the dynamics of plate tectonics present at Earth are not observed at Venus.  Gravity and topography are key observations to help understand the interior dynamics of a planet. On Earth, the long-wavelength geoid and total surface topography are not well correlated, with the interpretation that total surface topography is mainly due to the ocean-continent dichotomy whereas geoid reflects density anomalies deep in the mantle, mainly caused by subducted slabs. Dynamic surface topography is small compared to the total surface topography. On Venus, in contrast, the geoid and topography are well correlated, indicating a more direct connection between convection and the lithosphere and crust.

For Venus, two end-member origins of geoid and topography variations have been proposed: 1) Deep-seated (i.e. below the lithosphere) density anomalies associated with mantle convection, which may require a recent global lithospheric overturn to be significant [1][2][3]. 2) Variations in lithosphere and crustal thickness that are isostatically compensated - the so-called "isostatic stagnant lid approximation" [4][5], which appears consistent with simple stagnant-lid convection experiments.

Here we analyse 2-D and 3-D dynamical thermo-chemical models of Venus' mantle and crust that include melting and crustal production, multiple composition-dependent phase transitions and strongly variable viscosities to test whether variations in crust and lithosphere thickness explain most of the geoid signal [4][5], or whether it is caused mostly by density variations below the lithosphere, and thus, what we can learn about the crust, lithosphere and deeper interior of Venus from observations, as well as which tectonic mode is most likely to explain the observed geoid signal. Multiple input parameter sets are used to recreate the end-member scenarios of stagnant-lid and episodic-lid tectonics and to investigate the influence of the different rheological parameters. Characteristic snapshots of simulations showing end-member tectonic behaviour are analysed to determine the depth ranges of heterogeneities that are the predominant influence on topography and geoid variations. Findings will also guide future efforts to combine gravity and topography observations to infer lithosphere and crustal thickness and their variations (e.g. [6][7]).

References

[1] Armann, M., and P. J. Tackley (2012), Simulating the thermo-chemical magmatic and tectonic evolution of Venus' mantle and lithosphere: two-dimensional models, J. Geophys. Res., 117, E12003, doi:12010.11029/12012JE004231

[2] King, S. D. (2018), Venus resurfacing constrained by geoid and topography, J. Geophys. Res., 123, doi:10.1002/2017JE005475.

[3] Rolf, T., B. Steinberger, U. Sruthi, and S. C. Werner (2018), Inferences on the mantle viscosity structure and the post-overturn evolutionary state of Venus, Icarus, 313, 107-123, doi:10.1016/j.icarus.2018.05.014.

[4] Orth, C. P., and V. S. Solomatov (2011), The isostatic stagnant lid approximation and global variations in the Venusian lithospheric thickness, Geochem. Geophys. Geosyst., 12(7), Q07018, doi:10.1029/2011gc003582.

[5] Orth, C. P., and V. S. Solomatov (2012), Constraints on the Venusian crustal thickness variations in the isostatic stagnant lid approximation, Geochemistry, Geophysics, Geosystems, 13(11), n/a-n/a, doi:10.1029/2012gc004377

[6] Jiménez-Díaz, A., J. Ruiz, J. F. Kirby, I. Romeo, R. Tejero, and R. Capote (2015), Lithospheric structure of Venus from gravity and topography, Icarus, 260, 215-231, doi:10.1016/j.icarus.2015.07.020.

[7] Yang, A., J. Huang, and D. Wei (2016), Separation of dynamic and isostatic components of the Venusian gravity and topography and determination of the crustal thickness of Venus, Planetary and Space Science, 129, 24-31, doi:10.1016/j.pss.2016.06.001.

How to cite: Elbertsen, R., Tackley, P., and Rozel, A.: Geoid and topography on Venus: Isostatic or dynamic?, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-560, https://doi.org/10.5194/epsc2021-560, 2021.

Introduction: Although Venus shares many similar characteristics with Earth, like its size, distance to sun, and bulk composition, its surface characteristics significantly differ from those on Earth, especially in the lack of plate tectonics. From a geodynamic perspective, Venus has been proposed to be in an episodic-lid regime with catastrophic resurfacing and episodic overturns for the lithosphere (e.g., Armann & Tackley, 2012). However, these global models assumed that Venus’ crust has the same rheology as olivine and neglect dislocation creep, resulting in negligible deformation between overturn events, whereas in contrast, Venus' crust exhibits substantial tectonic deformation (e.g. Ivanov and Head, 2011; Ghail, 2015) and regional geodynamic models assuming a realistic, laboratory experiment-based crustal rheology and igneous intrusion into the crust, successfully reproduce surface features like coronae (Gerya, 2014; Gülcher et al., 2020). Therefore, in this study, we test the influence of a strain-rate dependent laboratory experiment-based rheology for the crust, as well as intrusive volcanism, in global geodynamic models to evaluate whether these factors could affect Venus’ tectonics and evolution, and help to explain Venus’ surface characteristics. 

Methods: We use the mantle convection code StagYY (Tackley, 2008) in a 2D spherical annulus geometry to model the thermochemical evolution of Venus. The infinite Prandtl number approximation is assumed, and compressibility is included in the model by assuming anelastic approximation.

A composite rheology is assumed, including diffusion creep, dislocation creep, and plastic yielding (using an effective rheology). This rheology depends on composition via the olivine and pyroxene-garnet phase systems, in both solid and molten states. For the basaltic crust, a plagioclase (An75) rheology from (Ranalli, 1995) as used in (Gülcher et al., 2020) is applied to the basalt facies in the pyroxene-garnet system. For other facies in pyroxene-garnet and olivine system, the rheological parameters are based on (Karato & Wu, 1993) for the upper mantle and (Yamazaki & Karato, 2001; Ammann et al., 2010) for the lower mantle. Additionally, we include intrusive magmatism in the model using an approach similar to (Lourenço et al., 2020).

Preliminary results and discussions: For the resurfacing history for Venus, the models show that if both dislocation creep rheology and plastic yielding plus intrusion magmatism are included, there would be both catastrophic global overturns with extensive magmatism (Figure 1) and localized resurfacings (Figure 2) during Venus’ mantle evolution. These two types of resurfacing are also shown in the time series of conductive heat flux (Figure 3 and 4): the conductive heat flux is much larger for global overturn due to extensive intrusive magmatism. Additionally, the surface mobilities in our models (Figure 3 and 4) differ from surface mobilities in olivine-crustal-rheology models, where the global overturns are followed by stagnant-lid phases with near-zero surface mobilities. Applying the realistic rheology (instead of olivine diffusion-creep rheology) to the crust could lead to a transition from near episodic-lid resurfacing (Figure 3) to a scenario with more local resurfacings and generally higher and more continuous surface mobilities (Figure 4).

Contrary to the previous global models (Armann & Tackley, 2012), there are no persistent mantle plumes in our models. Basalt accumulating at the boundary between upper and lower mantle (e.g. in Figure 2) works as a barrier for convective flows and affects mantle upwelling from the core-mantle boundary. Also, even if the intrusion depth is set to be below the basaltic crust (possibly, most of the intrusions solidify to form basaltic crust there), there could still be melt present in the crust (Figure 5). These short-term crustal melting events are in accord with observations of recent magmatic features found on Venus’ surface, and the short-term plumes suggested by coronae formation models (Gerya, 2014; Gülcher et al., 2020)