OPS1

The investigation of Titan’s surface chemical composition is of great importance for the understanding of the atmosphere-surface-interior system of the moon. The Cassini cameras and especially the Visual and infrared Mapping Spectrometer has provided a sequence of spectra showing the diversity of Titan’s surface spectrum from flybys performed during the 13 years of Cassini’s operation. In the 0.8-5.2 μm range, this spectro-imaging data showed that the surface consists of a multivariable geological terrain hosting complex geological processes. The data from the seven narrow methane spectral “windows” centered at 0.93, 1.08, 1.27, 1.59, 2.03, 2.8 and 5 μm provide some information on the lower atmospheric context and the surface parameters. Nevertheless, atmospheric scattering and absorption need to be clearly evaluated before we can extract the surface properties. In various studies (Solomonidou et al., 2014; 2016; 2018; 2019; 2020a, 2020b; Lopes et al., 2016; Malaska et al., 2016; 2020), we used radiative transfer modeling in order to evaluate the atmospheric scattering and absorption and securely extract the surface albedo of multiple Titan areas including the major geomorphological units. We also investigated the morphological and microwave characteristics of these features using Cassini RADAR data in their SAR and radiometry mode. Here, we present a global map for Titan’s surface showing the chemical composition constraints for the various units. The results show that Titan’s surface composition, at the depths detected by VIMS, has significant latitudinal dependence, with its equator being dominated by organic materials from the atmosphere and a very dark unknown material, while higher latitudes contain more water ice. The albedo differences and similarities among the various geomorphological units give insights on the geological processes affecting Titan’s surface and, by implication, its interior. We discuss our results in terms of origin and evolution theories.

References: [1] Solomonidou, A., et al. (2014), J. Geophys. Res. Planets, 119, 1729; [2] Solomonidou, A., et al. (2016), Icarus, 270, 85; [3] Solomonidou, A., et al. (2018), J. Geophys. Res. Planets, 123, 489; [4] Solomonidou, A., et al. (2020a), Icarus, 344, 113338; [5] Solomonidou, A., et al. (2020b), A&A 641, A16; [6] Lopes, R., et al. (2016) Icarus, 270, 162; [7] Malaska, M., et al. (2016), Icarus 270, 130; [8] Malaska, M., et al. (2020), Icarus, 344, 113764.

Acknowledgements: This work was conducted at the California Institute of Technology (Caltech) under contract with NASA. Y.M. and A.S. (partly) was  supported by the Czech Science Foundation (grant no. 20-27624Y). ©2021 California Institute of Technology. Government sponsorship acknowledged.

How to cite: Solomonidou, A., Coustenis, A., Le Gall, A., Lopes, R., Malaska, M., Schmidtt, B., Lawrence, K., Elachi, C., Schoenfeld, A., Sotin, C., Wall, S., Markonis, Y., and Matsoukas, C.: Compositional mapping of Titan’s surface using Cassini VIMS and RADAR data, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-137, https://doi.org/10.5194/epsc2021-137, 2021.

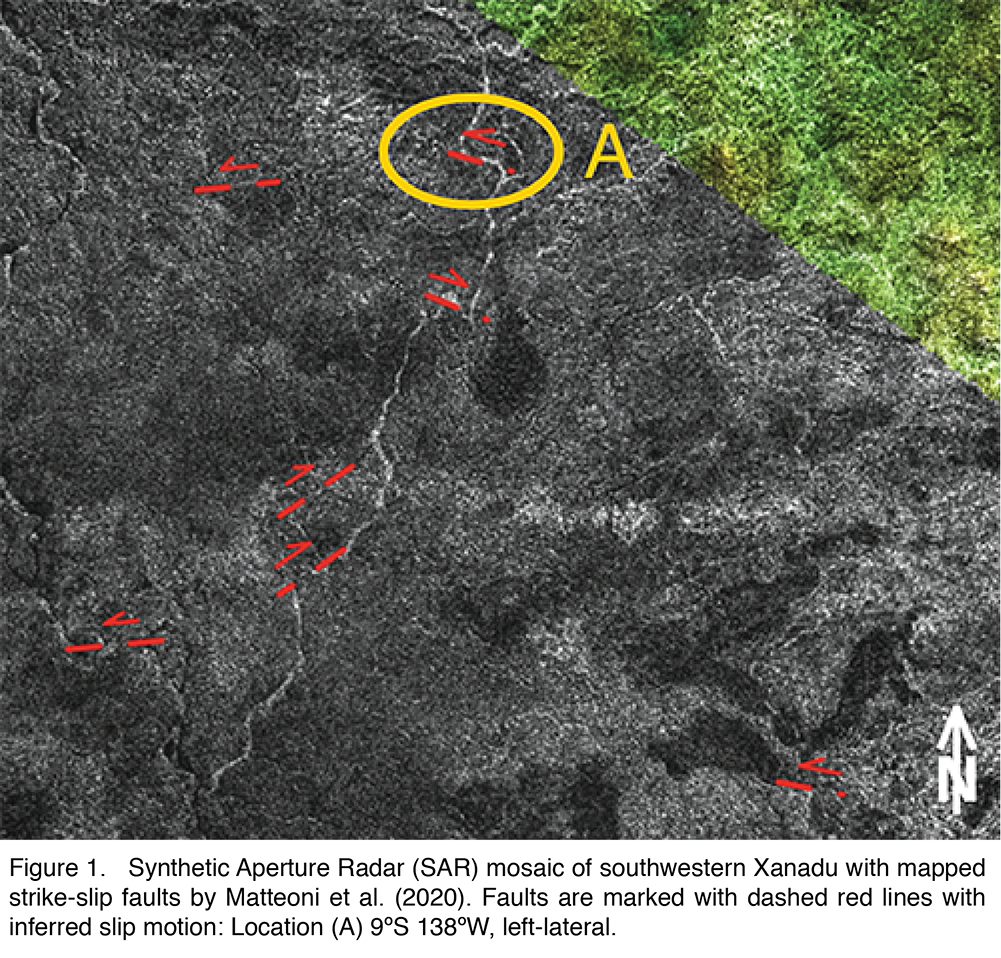
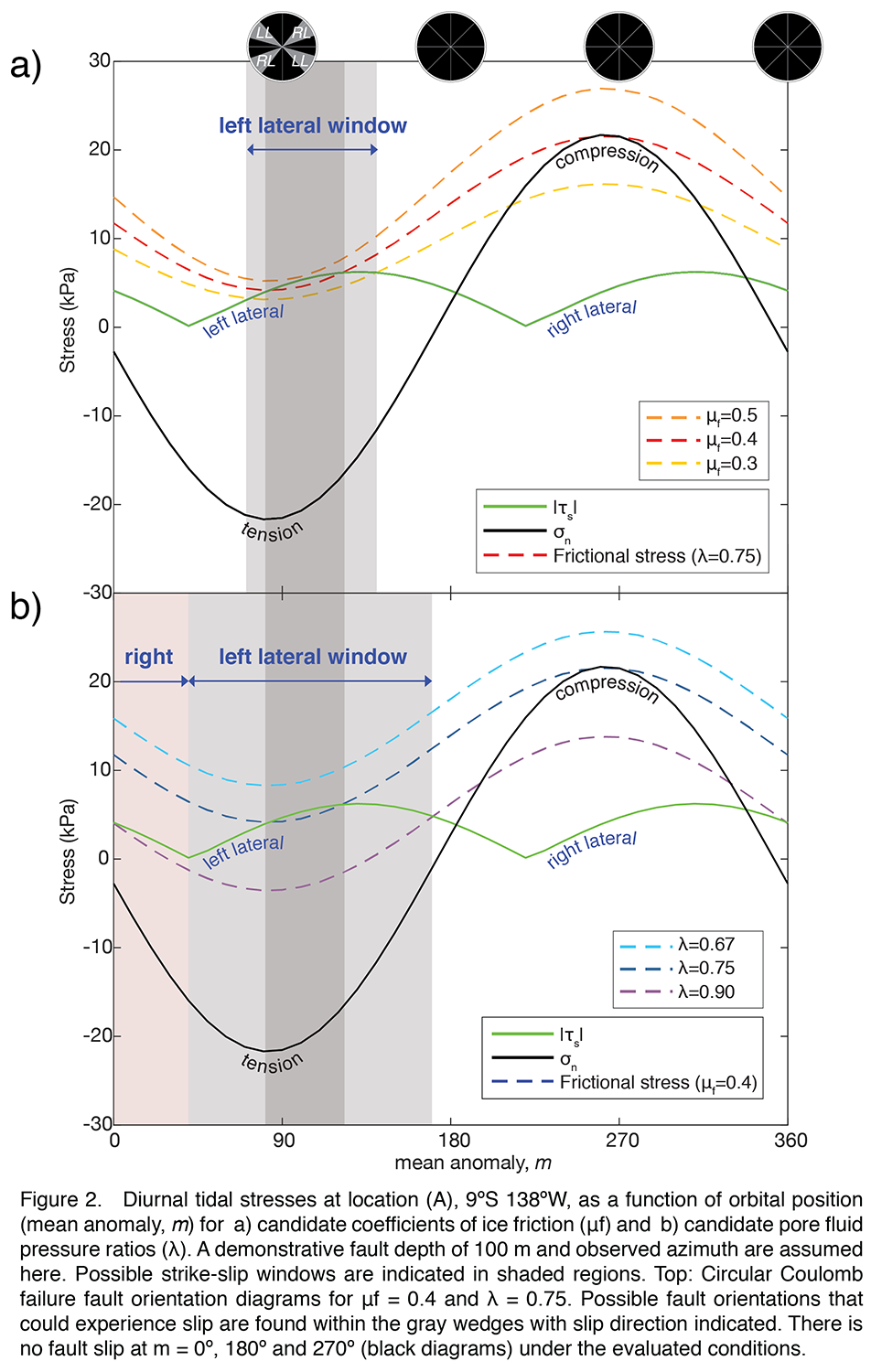
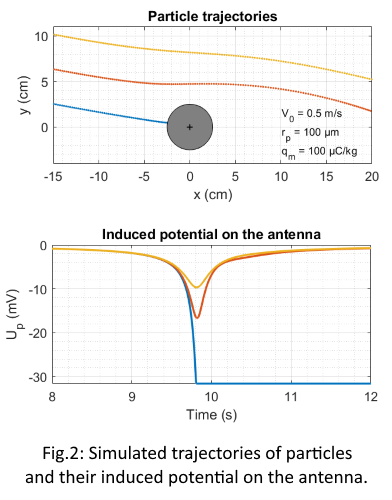
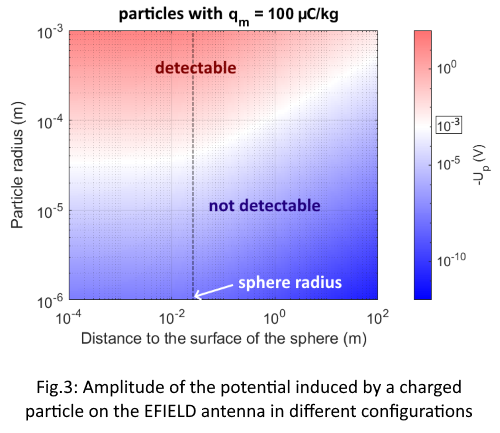
INTRODUCTION

The thermo-mechanical evolution of Titan's ice shell is primarily controlled by the mode of the heat transfer in the ice shell and the amount of heat coming from the ocean. Numerical models of thermal convection in Titan's ocean have suggested that the heat flux from the core can be strongly affected by the Coriolis effect, leading to a latitudinal gradient in the heat flux at the base of the ice shell [1,2,3]. These heat flux variations are of the order of mW/m² and may induce phase changes at the ice/ocean interface, affecting the thickness of the ice shell. Until now, the effect of lateral variations in the heat flux has been studied under the assumption that the ice shell is highly viscous and the heat transfer in the ice occurs by conduction. In such a case, the heat flux from the ocean is negatively correlated with the ice shell thickness [3]. A higher-than-average heat flux in polar regions then causes melting of ice and thinning of the ice shell, possibly explaining the fact that the poles on Titan are about 300 m lower than the equator [4].

The issue of whether Titan's ice shell is convecting or not has not yet been resolved. The mode of heat transfer depends on the ice shell thickness and the viscosity of ice, which in turn depends on the grain size and the temperature of the ocean. Since these parameters are not accurately known, the convection model cannot be excluded from analysis. The response of the convecting ice shell to heat flux variations from the ocean is likely to be different from that described for the conduction model [5]. When heat is transferred by convection, the ice shell is on average warmer and less viscous than in the conductive case. The loss/gain of ice mass at the ice/ocean interface caused by melting/freezing is compensated by flow of low-viscosity ice and, therefore, the shape of the ice/ocean interface remains unchanged. The shape of the surface topography is difficult to assess a priori because it may depend on the vigor of convection.

METHOD

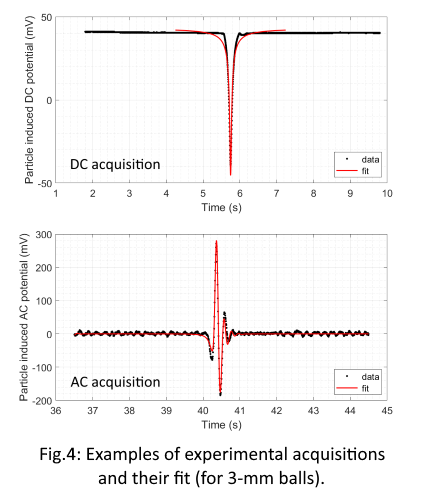
In this study, we investigate the effect of spatial variations in the heat flux from the ocean on the behavior of a convecting ice layer. The models discussed below have been obtained by simultaneously solving the momentum equation, the transport equation for temperature and the mass conservation equation for an incompressible fluid. The temperature is fixed to 90 K on the upper boundary and to 265 K on the bottom (ice/ocean) boundary. The computational domain is 100 km thick and has an aspect ratio of 16:1. We assume that the deformation of ice is controlled by diffusion creep and the viscosity of ice only depends on temperature and grain size.

The surface is treated as a material boundary while the ice/ocean interface is open and its shape can change due to phase changes. The heat flux variations from the ocean enter the problem through the energy conservation law which relates the jump in the heat flux across the boundary with the relative motion of the ice/ocean interface [3,6,7]. Note that the heat flux across the phase boundary is generally not continuous (as assumed, for example, by [8]), but depends on the velocity of ice flow, which cannot be neglected if the viscosity of ice is low (< 10¹⁶ Pa.s). The lateral variation of the heat flux imposed at the bottom boundary of the domain is scaled to correspond to 50 % of the average heat flux (Fig. 1a).

RESULTS

In Figs. 1 and 2, we compare the results obtained for a grain size of 2 mm and 3 mm. Although these values are close to each other, the models represent two end-member cases discussed above. While in the former case (2 mm), the heat transfer is controlled by convection, in the latter case (3 mm), convection does not develop and the heat is transferred by conduction.

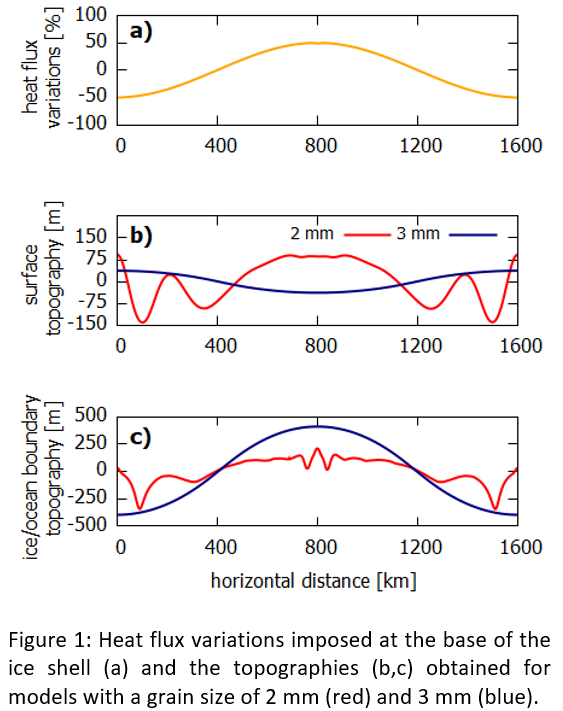
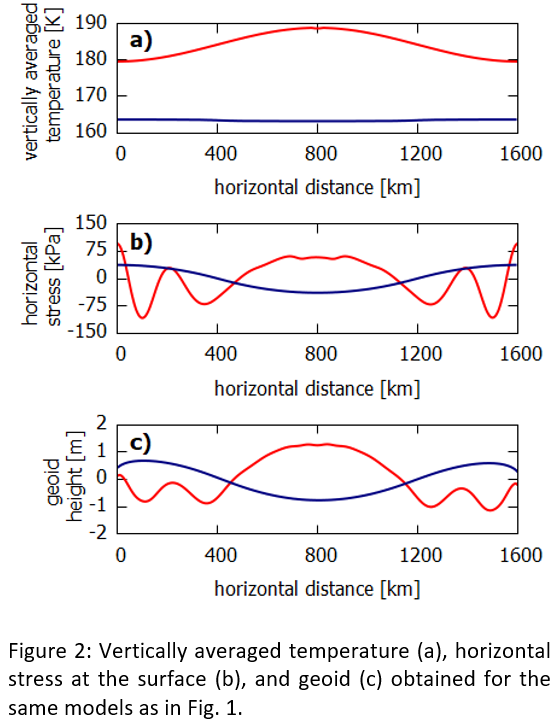
Inspection of Figs. 1 and 2 shows that the convection model gives the opposite sign of the surface topography than the conduction model (Fig. 1b) and predicts a significant (8 K) increase in ice temperature above the positive heat flux anomaly (Fig. 2a). The conduction and convection models also give different orientations of tectonic stresses - extension in the case of convection and compression in the case of conduction (Fig. 2b). Both models predict only small amplitudes of the geoid (Fig. 2c), suggesting that the equilibrium state can be approximated by either Airy or Pratt isostatic model, depending on the mode of heat transfer.

CONCLUSIONS

Variations in the heat flux from the ocean can significantly influence Titan’s topography and the distribution of stress near the surface. The topography is negatively correlated with the heat flux when the heat in the ice shell is transferred by conduction, whereas a positive correlation and more complex topography response is found for the convective heat transfer.  In contrast to the topography, the heat flux variations have only a small effect on the geoid. A careful analysis of the geoid and topography data collected by Cassini could thus provides an insight into the processes occurring in Titan's interior and helps answer the question of which heat transfer mode dominates in Titan's ice shell.

ACKNOWLEDGEMENTS

This research was supported by the Czech Science Foundation through project No. 19-10809S. M.K. acknowledges the support from the Charles University project SVV-2020-260581. K.K. was supported by the Charles University Research program No. UNCE/SCI/023. G.C. and G.T. acknowledge the support from the ANR COLOSSe project. 

REFERENCES

[1] Soderlund, 2019, Geophys. Res. Lett. 46, 8700–8710.

[2] Amit et al., 2020, Icarus 338, 113509.

[3] Kvorka et al., 2018, Icarus 310, 149–164.

[4] Corlies et al., 2017, Geophys. Res. Lett. 44, 11754–11761.

[5] Nimmo and Bills, 2010, Icarus 201, 896–904.

[6] Čadek et al., 2019a, Icarus 319, 476–484.

[7] Čadek et al., 2019b, Geophys. Res. Lett. 46, 14299–14306.

[8] Ojakangas and Stevenson, 1989, Icarus 81, 242–270.

How to cite: Kihoulou, M., Čadek, O., Kalousová, K., Choblet, G., and Tobie, G.: Effect of ocean heat flux on Titan's topography and tectonic stresses, Europlanet Science Congress 2021, online, 13–24 Sep 2021, EPSC2021-155, https://doi.org/10.5194/epsc2021-155, 2021.

Titan's geology is complex, with a wide range of surface morphology, including fluvial, aeolian, and cryovolcanic and tectonic activity. Surface observations have not yet revealed large-scale and distinct characteristics of strike-slip faulting (i.e., en echelon structures, fault duplexes, and clear offset features) that have been observed on other ocean worlds such as Europa, Ganymede, and Enceladus [1,2]. However, the SW Xanadu region shows offsets in fluvial networks that seem to have been caused by strike-slip faulting [3]optimal shear failure conditions may be present within Titan's shallow subsurface, where the existence of a porous ice cover filled with liquid hydrocarbons can create an environment for areas of frictional instability [4], shear heating [5], and possibly cryovolcanism [6,7]. In this work, we examine Titan’s ability to host shear deformation at identified rectilinear fluvial features that are inferred to be strike-slip faults [3] through a sensitivity analysis guided by Coulomb failure laws [8] and tidal stress mechanisms [9]. Our modeling technique includes considerations for how the presence of near-surface liquid hydrocarbons and the crustal porosity of the ice significantly reduce the resistance to shear failure of strike-slip faults subjected to diurnal tidal stresses through a pore pressure parameter.

For this study, we examine failure conditions at proposed example strike-slip faults [3] in SW Xanadu (Figure 1): (A) 9ºS 138ºW. Using the SatStress [9,10] tidal stress model for Titan-appropriate rheology [6], we compute the diurnal tidal stress tensor and resolve shear and normal stresses onto shallow fault planes (100 m depth) with azimuthal orientations consistent with mapped observations [3], as well as for the full range of orientations. We explore candidate coefficients of friction (μ_f= 0.3-0.5) [11] and hydrostatic pore fluid pressure ratios for Titan (l = 0.67-0.9) [4]. Figure 2 illustrates where the magnitudes of frictional stress and absolute value of shear stress overlap and the Coulomb criterion is met using the mapped azimuth of the suggested fault structure, permitting a finite slip-window. At a shallow fault depth of 100 m and for the inferred oriented faults, our model suggests that shear failure is possible under diurnal tidal stresses subjected to the studied parameters. For an assumed coefficient of friction of μ_f = 0.4, shear failure can only be achievable with intermediate to high pore fluid pressure ratios (λ > 0.75). At location (A), the resulting left-lateral slip direction from the model agrees with the inferred left-lateral shear direction of the proposed mapped strike-slip fault [3]. However, right- and left-lateral slip windows are achieved for a range of possible azimuths at this location with μ_f = 0.4 and a pore fluid pressure ratio of l = 0.75 (Figure 2, top). While a variety of factors can control this observed fluvial drainage system on Titan, the general azimuthal orientation of these features in this region suggests that there is a subsurface tectonic fabric trending roughly east-west guiding the flow of these rectilinear fluvial systems. Overall, our findings show that on Titan, the crustal porosity of ice and the inclusion of near-surface liquids will minimize the resistance to shear failure of faults subjected to diurnal tidal stresses. The optimal combination of tensile and shear tractions can allow for finite slip windows where the Coulomb criteria is met.

References:  [1] Cameron, M.E. et al. (2018) Icarus, 315, 92-114.  [2] Martin, E.S. (2016) Geophys. Res. Let., 43, 2456–2464.  [3] Matteoni, P. et al. (2020) JGR: Planets, 125(12).  [4] Liu, Z. et al. (2016) Icarus, 270, 2-13.  [5] Nimmo, F. et al. (2007) Nature, 447, 289.  [6] Sohl, F. et al. (2014) JGR: Planets, 119, 1013-1036.  [7] Malaska, M.J. et al. (2016) Icarus, 270, 130-161.   [8] Byerlee, J. (1978) Pageoph, Vol. 116.  [9] Wahr, J. et al. (2009) Icarus, 200, 188-206. [10] Patthoff, A. et al. (2016) AGU, Abstract #P51B-2147.  [11] Schulson, E.M. (2016) Int. Material Reviews, 60:8, 451-478.