The two parameterisations of the Andrade rheological model in planetary science: a comparative study

Measuring the global deformation in response to periodic tidal loading belongs to the geophysical methods devised for probing the interior structure of celestial bodies. The response depends on the magnitude and frequency of loading as well as on the microphysical deformation mechanisms involved. Throughout the past ten years, it has proven useful and become popular to characterise the planet’s reaction by the Andrade rheological model (Andrade, 1910; Jackson & Faul, 2010; Castillo-Rogez et al., 2011; Efroimsky 2012a,b). The model is able to predict the correct frequency dependence of attenuation in polycrystalline solids and does not underestimate the high-frequency tidal dissipation, as it is the case with the simpler Maxwell viscoelastic model (see the discussion in, e.g., Renaud & Henning, 2018). However, the ways the Andrade model is parameterised in planetary science diverge.

Within the first parameterisation, the standard formula for the Andrade compliance used in material science (e.g., Jackson & Faul, 2010) is applied and the effect of temperature, pressure, and grain size on the response is included through pseudo-period master variable:

X_B = T₀ (d/d_R)^-m exp{-E^*/R (1/T-1/T_R)} exp{-V^*/R (P/T-P_R/T_R)}                (1)

A complication might occur when combining the rheological model with an outcome from thermal evolution codes: the reference parameters and the implied Arrhenian viscosity law used in equation (1) are typically different from the values considered in thermal modelling, which might lead to inconsistencies. However, when only used within the tidal framework and with a fixed interior structure, this “α-β approach” yields useful predictions and is traditionally applied in studies of terrestrial planets and the Moon (e.g., Nimmo et al., 2012; Padovan et al., 2014; Steinbrügge et al., 2018; Bagheri et al., 2019).

In the second case, a new parameter ζ is introduced (Efroimsky, 2012a), where ζ=1 corresponds to the fit to experimental data presented by Castillo-Rogez et al. (2011). The advantage of the reparameterisation is the substitution of a parameter with a fractional dimension (β) with a parameter that has a clearer physical interpretation: ζ specifically represents the ratio of the characteristic anelastic and viscoelastic deformation timescales. This approach only takes the grain size into account through the actual viscosity profile and does not require the introduction of a pseudo-period. Therefore, it can be more easily linked to the viscosity profiles outputted by thermal evolution models. The “α-ζ approach” has been considered by several studies of layered icy bodies and also applied to Venus and terrestrial exoplanets (Castillo-Rogez et al., 2011; Dumoulin et al., 2017; Tobie et al., 2019; Bolmont et al., 2020).

Here, we compare the tidal deformation and dissipation within several solar system bodies (with a special focus on Moon and Mars), calculated in the two approaches and using typical values of the parameters α, β, and ζ and viscosity laws considered in the literature. An illustration of this comparison is presented in Figure 1. We evaluate the differences in the resulting tidal parameters and endeavour to find a mapping between the global response models with constant ζ and the models with constant β that use the pseudo-period (1). The understanding of the different parameterisations, the way they are used in planetary science in combination with the thermal evolution models, and eventually the depth-dependence of the relevant variables, may provide valuable insights into the link between microphysical deformation mechanisms and the observed tidal deformation.

 

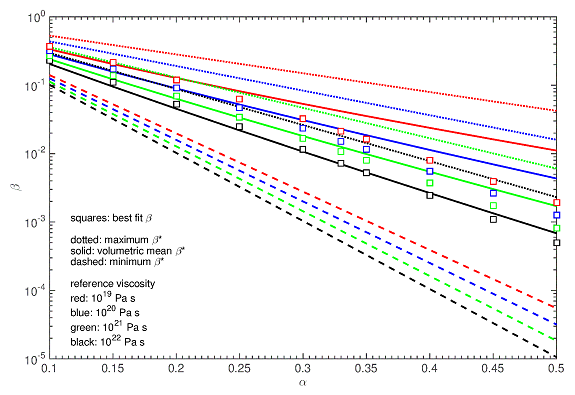
Figure 1: Preliminary comparison of the two parameterisations. Lines indicate the minimum, maximum, and volumetrically averaged value of β that would correspond to a constant (depth-independent) ζ in a layered interior model (depending on the parameter α and on the local temperature and pressure). Squares indicate the values of β which, used together with the pseudo-period (1), best fit the tidal Love number k₂ calculated within the α-ζ approach with constant ζ.

 

References

Andrade, E. N. D. C. (1910) Proceedings of the Royal Society of London Series A, vol. 84, no. 567, pp. 1–12.

Bagheri, A., Khan, A., Al-Attar, D., Crawford, O., and Giardini, D. (2019) Journal of Geophysical Research (Planets), vol. 124, no. 11, pp. 2703–2727. doi:10.1029/2019JE006015.

Bolmont, E., Breton, S. N., Tobie, G., Dumoulin, C., Mathis, S., and Grasset, O. (2020) Astronomy and Astrophysics, vol. 644. doi:10.1051/0004-6361/202038204.

Castillo-Rogez, J. C., Efroimsky, M., and Lainey, V. (2011) Journal of Geophysical Research (Planets), vol. 116, no. E9. doi:10.1029/2010JE003664.

Dumoulin, C., Tobie, G., Verhoeven, O., Rosenblatt, P., and Rambaux, N. (2017) Journal of Geophysical Research (Planets), vol. 122, no. 6, pp. 1338–1352. doi:10.1002/2016JE005249.

Efroimsky, M. (2012a) Celestial Mechanics and Dynamical Astronomy, vol. 112, no. 3, pp. 283–330. doi:10.1007/s10569-011-9397-4.

Efroimsky, M. (2012b) The Astrophysical Journal, vol. 746, no. 2. doi:10.1088/0004-637X/746/2/150.

Jackson, I., Faul, U. H., Suetsugu, D., Bina, C., Inoue, T., and Jellinek, M. (2010) Physics of the Earth and Planetary Interiors, vol. 183, no. 1–2, pp. 151–163. doi:10.1016/j.pepi.2010.09.005.

Nimmo, F., Faul, U. H., and Garnero, E. J. (2012) Journal of Geophysical Research (Planets), vol. 117, no. E9. doi:10.1029/2012JE004160.

Padovan, S., Margot, J.-L., Hauck, S. A., Moore, W. B., and Solomon, S. C. (2014) Journal of Geophysical Research (Planets), vol. 119, no. 4, pp. 850–866. doi:10.1002/2013JE004459.

Renaud, J. P. and Henning, W. G. (2018) The Astrophysical Journal, vol. 857, no. 2. doi:10.3847/1538-4357/aab784.

Steinbrügge, G., Padovan, S., Hussmann, H., Steinke, T., Stark, A., and Oberst, J. (2018) Journal of Geophysical Research (Planets), vol. 123, no. 10, pp. 2760–2772. doi:10.1029/2018JE005569.

Tobie, G., Grasset, O., Dumoulin, C., and Mocquet, A. (2019) Astronomy and Astrophysics, vol. 630. doi:10.1051/0004-6361/201935297.