A parametric level-set approach to the global gravity inversion of small bodies

Introduction

Most spacecraft missions to small bodies provide the gravity field of their targets. As the extended gravity field is an expression of the mass distribution within the body, it can provide information about its interior structure, and that in turn can constrain its origin and history.

We present a method to detect density anomalies within a small body from the global gravitational potential. As is well known, such an inverse problem is ill-posed [1], and requires regularization. Our main assumption, which mitigates the non-uniqueness of the problem, is that the interior of the body is composed of a finite number of domains, in which the density is uniform. The boundary of each domain is therefore a surface, that we describe as the level-set of a function. This approach, known as the level-set method, has been extensively used in local inversions of Earth’s gravity measurements [2]. It simplifies the manipulation of complex shapes, which in our case delimit the density anomalies.  

In order to reduce the dimensionality of the problem, we employ parametric expressions for the level-set functions. The aim is then to determine the parameters of each level-set function, which describe the location and size of the anomalies, along with the density within each anomaly and the bulk density of the body.

 

Methods

We model the gravity field of the body through a mascons approach [3]. The observables we consider are the coefficients of the spherical harmonic expansion of the potential. By implementing a continuous approximation for the unit step function, the partials derivatives of the measurements with respect to the level-set function parameters can be computed via the chain rule [4]. Then, the function parameters and the densities can be estimated via non-linear least-squares inversion of the gravity data.

However, the problem is generally non-convex, which means that in order to converge to a global optimum the a priori values for the unknowns should be close to this solution. Since we assume no initial knowledge of the distribution to retrieve, a preliminary step is needed for the definition of an a priori model. To this end, we generate a Voronoi partition of the interior from randomly sampled points within the body. The domains are now fixed, and only the densities within each Voronoi cell are estimated from the data. This inversion problem is linear, but the solution will depend on the partition of the body. However, averaging solutions from many of such random partitions can provide a good approximation of the true model [5]. This averaged solution is then used to initialize the values of the level-set algorithm.

 

Discussion and outlook

We have tested the ability of our level-set implementation to retrieve interior models from simulated gravity data. 

Figure 1 shows an example of the inversion results for a Bennu-shaped body. In this case, the level-set functions are chosen so that the anomalies they describe are cuboids. The model in Figure 1a is the ground truth, used to simulate gravity coefficients up to degree 11. Figure 1b shows the density retrieved from the noise-free data, and Figure 1c the results when the data are perturbed by 1% Gaussian noise. The method can retrieve the location and density of the anomalies with good approximation, even in the perturbed case. For anomalies where the density and the size cannot be estimated simultaneously, such as with nearly-spherical shapes, the method can usually still correctly determine the total mass and the position of the center-of-mass. The size could then be constrained by independent observations from other instruments or by theoretical models.

In a more realistic scenario, the resolution of the gravity would be lower, and the noise profile would be increasing with the degree of gravity. This could aggravate the non-uniqueness problem, since having fewer and less precise measurements could lead to different models fitting the data equally well. Current work is focused on improving the robustness of our approach and on better defining its limitations in its application to real gravity measurements. 

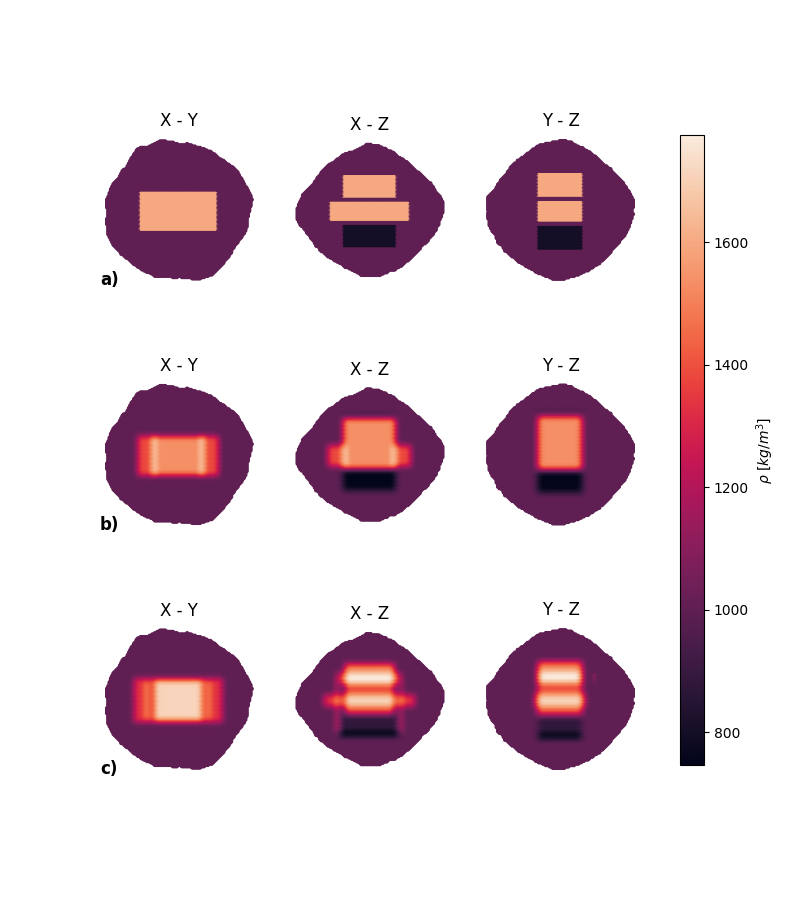
Figure 1. Interior density models, shown via sections along 3 planes perpendicular to the body axes and containing the origin: a) Ground truth; b) Solution from noise-free data; c) Solution from data with 1% noise

 

Acknowledgements

This work was financially supported by the French community of Belgium within the framework of a FRIA grant, and by the Belgian PRODEX program, managed by the European Space Agency in collaboration with the Belgian Federal Science Policy Office.

 

References

[1]  V. Isakov. Inverse Source Problems. American Mathematical Soc., 1990. 

[2]  J. Giraud, M. Lindsay, and M. Jessell. Generalization of level-set inversion to an arbitrary number of geologic units in a regularized least-squares framework. GEOPHYSICS, 86(4):R623–R637, July 2021. 

[3]  S. Le Maistre, A. Rivoldini, and P. Rosenblatt. Signature of Phobos’ interior structure in its gravity field and libration. Icarus, 321:272–290, March 2019.

[4]  A. Aghasi, M. Kilmer, and E. L. Miller. Parametric Level Set Methods for Inverse Problems. SIAM Journal on Imaging Sciences, 4(2):618–650, January 2011. 

[5]  L.-I. Sorsa, M. Takala, P. Bambach, et al. Tomographic inversion of gravity gradient field for a synthetic Itokawa model. Icarus, 336:113425, January 2020.