Constraints on the lunar magnetic sources location using orbital magnetic field data

Introduction

Spacecraft measurements show heterogeneously distributed magnetic field signals [1] indicative that the surface of the Moon is, at least, locally magnetized. The sources of those magnetic anomalies are yet not fully understood, as most of them are not related to known geological structures or processes (e.g. swirls). Some hypothesis to explain the origin of the magnetic sources include contamination from impactors that could deliver iron-rich material to the lunar surface [2], and heating associated with localized magmatic activity that could thermochemically alter rocks to produce strong magnetic carriers [3]. However, for both cases, an inducing field that could magnetize the lunar crust, such as a global magnetic field generated by a core dynamo, is required.

How a body gets magnetized depends on which geological processes occur, and different conclusions can be reached depending on the magnetization type. For example, for a thermoremanently magnetized terrain, magnetic information is valuable to constraint the paleopole position of a dipolar ambient magnetic field present during the geological process [e.g. 4, 5]. Some magnetic anomalies are associated with swirls which can help to constrain the sources geometry [3]. However, many other isolated anomalies are not, precluding us to constrain the sources shape. Here we propose another method, which is not dependent on the association of magnetic anomalies with swirls or geological structures, to elucidate the origin of the magnetic sources by constraining the location and geometry of the underlying magnetization.

 

Method

The magnetization geometry is inferred from orbital synthetic magnetic field measurements using an inversion scheme that assumes unidirectional magnetization while making no a priori assumptions about its shape [6]. This method has been previously used to infer the direction of the underlying magnetization [4-8] but it has not been used to infer the geometry of the sources.

The performance of the method is tested by conducting a variety of inversions. First, we build synthetic magnetic field observation grids, resulting from known buried uniformly magnetized bodies of different geometries. Three main geometries are used to mimic the main geological structures potentially magnetized at the lunar crust. Those are thin vertical cylinders, parallelepipeds and half horizontal cylinders to mimic basins, dykes, and lava tubes, respectively. For each case, we vary the thickness, the depth to the top layer and the horizontal size of the magnetized body, as well as the inducing field direction. To mimic the lunar case [4] for each uniformly magnetized body buried in the planet, the input synthetic magnetic observations are distributed in a grid at 30km altitude whereas the a priori dipoles mesh is placed at the surface. The best fitting direction of magnetization and the corresponding nonnegative dipoles distribution solution, is obtained from a nonnegative least squares inversion.

 

Results

Results from our synthetic tests show that this method is able to recover the location of the buried magnetized body. As an example, Figure 1 shows that stronger nonnegative dipoles from the best fitting solution are lying over the uniformly magnetized half horizontal cylinder. Figure 2 shows the  sum of dipole moments as a function of longitude and latitude when varying the depth of the half horizontal cylinder magnetized body.

In general, we find in our inversions results a good correlation between the positions of the stronger dipole moments and the magnetized body, for the three tested shapes. When varying the thickness of the magnetized body, we find that thicker the body is, stronger are the dipole moments over the location of the body. When varying the depth of the body from 10 km to 60 km under the surface, the method retrieves correctly the position of the magnetized body although the accuracy on locating the body slightly decreases at same time that the strength of the dipole moments diminishes. By varying the magnetization direction from 0º to 180º from vertical, the method correctly retrieves the position of the magnetized body, however is less performant when the magnetization is horizontal to
the surface.

Figure 1: Best fitting inversion solution for a uniformly magnetized half horizontal cylinder at 10 km depth, radius of 1 degree, and magnetization vector pointing radially out from the surface. Dipole moments distribution as a function of (left) longitude and (middle) latitude. Distribution of nonnegative dipoles at the surface (right) where stronger dipoles are in hot colors.

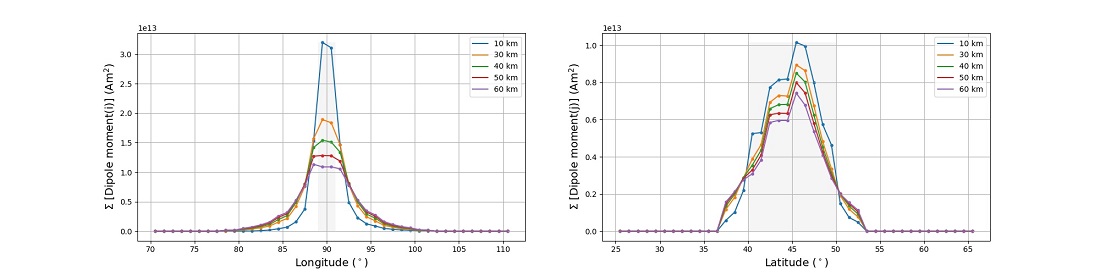
Figure 2: Sum of the dipole moments of the best-fit solution as a function of (left) longitude and (right) latitude, for the horizontal half cylinder case where depth varies (each depth corresponds to a color). Bins of 1 degree are used. Gray shadow locates the buried magnetized body.

 

Conclusion

The Parker’s method [6] initially designed to retrieve the magnetization direction of a uniformly magnetized body for paleopole location purposes is surprisingly performant in locating the position of the magnetized material. Three different volumes representative of the main geological structures that might be magnetized on the lunar surface have been successfully tested. Such an analysis can be performed on many lunar magnetic anomalies, including those which are not related to swirls or impact craters, i.e., the mechanisms that have been most studied up to now. This will help to elucidate the geological history of the Moon and key features of the lunar dynamo evolution.

Acknowledgements JSO is funded by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement SIGMA no 893304. This work has been partially funded by the Spanish Programme for Research, Development and Innovation under the project MINOTAUR of reference PID2020-119208RB-I00.

 

Bibliography

[1] Tsunakawa, H. et al. (2015), JGR Planets, 120, 1160–1185, doi:10.1002/2014JE004785.

[2] Wieczorek, M. A. et al. (2012). Science, 335(6073), 1212–1215. https://doi.org/10.1126/science.1214773

[3] Hemingway, D. J., & Tikoo, S. M. (2018). JGR Planets, 123, 2223– 2241. https://doi.org/10.1029/2018JE005604

[4] Oliveira, J. S., and Wieczorek, M. A. (2017), JGR Planets, 122, 383– 399, doi:10.1002/2016JE005199.

[5] Oliveira, J. S. et al. (2019), JGR Planets, 10.1029/2019JE005938, 124, 9, (2382-2396).

[6] Parker, R. L. (1991), JGR, 96, 16,101–16,112, doi:10.1029/91JB01497.

[7] Oliveira, J. S., et al. (2017), JGR Planets, 122, 2429– 2444. https://doi.org/10.1002/2017JE005397

[8] Thomas, P. et al. (2018), JGR Planets, 123, 1140– 1155. https://doi.org/10.1002/2017JE005511