Averaged theory applied to the co-orbital motion of real asteroids in the solar system in the medium-term timescale

Abstract

The aim of this work is to investigate the dynamics of small bodies that are in co-orbital motion with a given planet in the solar system. The study is based on the data corresponding to the ephemerides computed by the JPL Horizons system for asteroids with a low inclination with respect to the Sun-planet orbital plane. These objects are cataloged according to their dynamics as seen in the averaged formulation of the Restricted Three-Body Problem in the circular-planar case. The tool developed can show where asteroids in horseshoe motion, quasi-satellite motion and tadpole motion are located, together with the dynamical transitions that occur in the given timeframe. The results will provide the first catalog of asteroids in co-orbital motion in the solar system at the moment and an efficient mean to study dynamical transitions. Moreover, for the Earth case, possible targets for future retrieval and exploration mission can be pinpointed.

Introduction

Co-orbital motion is a particular type of dynamics that occurs in the Three-Body Problem, according to which two bodies gravitate towards a more massive body with the same period. 
Many objects susceptible to be at least temporary co-orbitals have been observed in the solar system, in particular for Venus, Earth, Mars and Jupiter.
A major example is given by the Trojans of Jupiter, that move on tadpole (TP) trajectories in the neighborhood of the two Lagrange's equilateral configurations L₄ and L₅ in the synodic reference system. In the prograde case, the other two fundamental configurations are horseshoe (HS) trajectories and quasi-satellite (QS) orbits.

Co-orbital trajectories, their possible mutual transitions together with escaping/trapping mechanisms are not only evident in the natural dynamics observed in the solar system, but very recently they have also assumed an important role for space exploration missions. For instance, ESA is  planning to exploit L₅ of the Sun-Earth system to monitor the solar activity and the related space weather issues. The Chinese space agency aims at visiting the near-Earth asteroid Kamo'oalewa, due to its interesting QS state.

The idea of this work comes from the development of Pousse and coauthors [1,2], regarding the averaged Hamiltonian of the Restricted Three-Body Problem (RTBP) in the circular-planar case. From the theoretical point of view the domain of validity of the analytical model has been proved, here we are interested in testing its validity against real bodies dynamics and to propose some applications. The main tool we will consider is a simple map, that is function of the orbital eccentricity of the heliocentric motion of the asteroid and the relative phase between the planet and the asteroid, and that can comprise all the important information about the motion of the asteroid.

Methods

Taking as example a system composed by the Sun, a planet and an asteroid, we assume the RTBP approximation in the circular-planar case. Following the co-orbital assumption, the asteroid orbits the Sun with the same orbital period as the planet orbits the Sun. The resonant condition on the orbital periods allows for very stable solutions, that are indeed observed in the solar system, as mentioned above.

We are interested in depicting the dynamics of the asteroid with regard to the orbital elements associated with its heliocentric motion. In particular, since the motion is assumed to be planar, we will focus on its semi-major axis a and eccentricity e and an angle θ, related to the relative phase with respect to the motion of the planet. 
Since we focus on the co-orbital dynamics, that can be seen as the continuation of Keplerian orbits in 1:1 mean motion resonance with the planet, the most natural choice appears to tackle the problem by means of a perturbative treatment, considering the mass parameter of the system as the perturbative parameter. By adopting a suitable set of resonant variables and the possibility to separate different timescales, the dynamics can be described by a 1 degree-of-freedom integrable model, that allows to depict simple phase space portraits that catch the main secular features.

The instruments corresponding to the averaged perturbation theory are applied to the ephemerides computed by the JPL Horizons system over about 900 years for asteroids that can be in co-orbital motion with Venus, Earth, Jupiter or Saturn, with an inclination low enough to be considered almost coplanar with the given planet. The analysis aims at identifying the asteroids in 1:1 mean motion resonance at the current time, not only in TP motion, and to reveal the possible mechanisms of transitions (see an example in Fig. 1) between co-orbital configurations and not. In particular, we analyse the transitions with respect to the limits of our model (e.g., non-negligible inclination, or external effect).

Figure 1: Example of transition between horseshoe motion and quasi-satellite motion.

A simple map, function of (θ,e), is used to characterize the given Sun-planet system. The asteroids that are in co-orbital motion with Jupiter at an epoch corresponding to the actual one within a certain threshold are shown in Fig. 2.

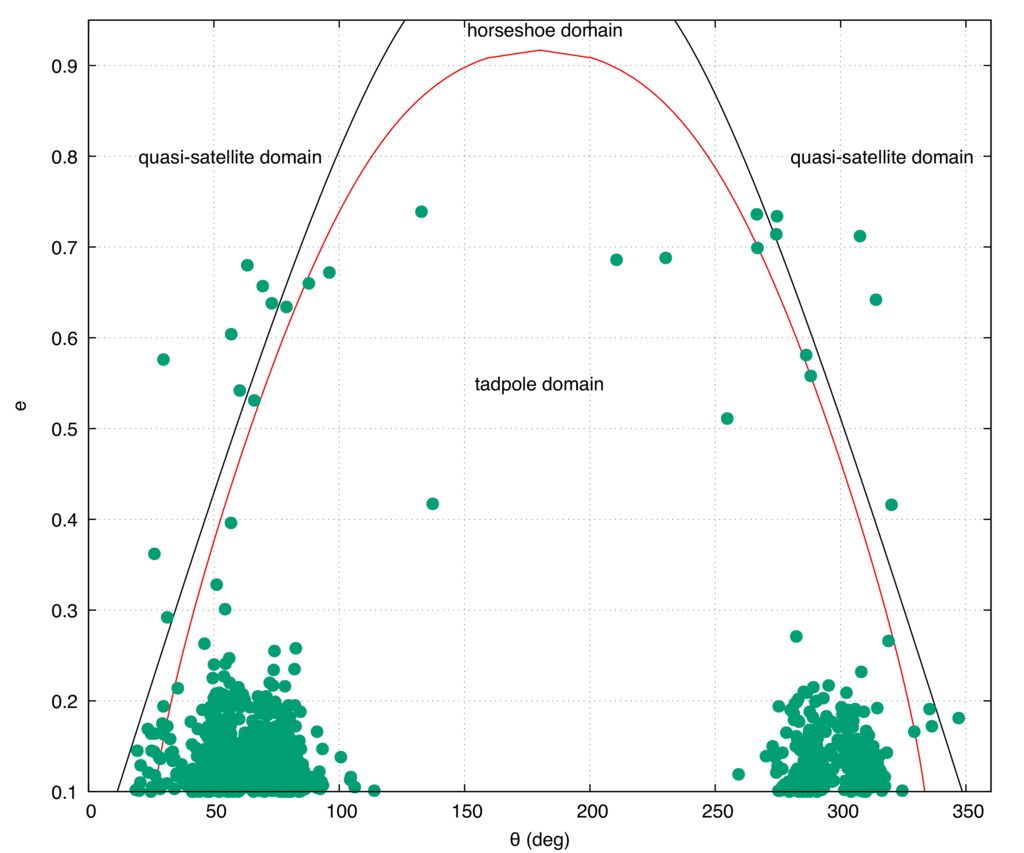
Figure 2: General map to represent the co-orbital asteroids for a given Sun-planet system. Here we show the results obtained for Jupiter in the almost co-planar case.

Acknowledgments
The authors are indebted with Federica Spoto from CFA Harvard and with Tommaso Del Viscio from IMATI-CNR. A.P and E.M.A. acknowledge the support received by the project entitled "co-orbital motion and three-body regimes in the solar system", funded by Fondazione Cariplo through the program "Promozione dell'attrattività e competitività dei ricercatori su strumenti dell'European Research Council - Sottomisura rafforzamento".

References

[1] Pousse A., Robutel P., Vienne A., On the co-orbital motion in the planar restricted three-body problem: the quasi-satellite motion revisited. Celest. Mech. Dyn. Astron. 128(4), 383-407 (2017)

[2] Pousse A., Alessi E.M., Revisiting the averaged problem in the case of mean-motion resonances in the restricted three-body problem. Nonlinear Dynamics 108, pages 959-985 (2022)